안녕하십니까. 고려대학교 산업경영공학부 석사과정, DSBA 연구원 윤훈상입니다. 이번 Paper review에서는 XGBoost에 대해서 알아보고자 합니다.
XGBoost는 확실히 저를 포함해 데이터 사이언스 또는 머신러닝을 공부하고 있는 사람이라면 한번이라면 들어봤을 이름입니다. Kaggle 등과 같은 머신러닝 대회 또는 공모전들에서 예측의 높은 성능을 위해 사용되기도 하고, 다양한 프로젝트에 적용되는 대표적인 Machine Learning Algorithm이기 때문입니다. 하지만 저는 본 기법을 사용함에 있어 결과물만 빠르게 내는 것에 급급하여, 이론적인 부분을 아주 간략하게만 접해왔습니다. 또한 Boosting 까지는 개념적으로 이해하고 있으며, 그것을 Extreme하게 합친 것이니 뭔가 더 좋겠지 라는 막연한 기대감에 원리를 파악하는 데에 소홀했습니다.
하지만 저자인 Tianqi Chen & Carlos Guestrin의 원 논문을 보고, 그것을 이해하기 위하여 다양한 참고자료를 검토한 결과, XGBoost는 Boosting에 비롯하기는 하지만 더 높은 차원의 알고리즘이라는 것을 알게 되었습니다. 또한 논문의 난이도가 예상보다 높아, 알고리즘 자체도 Extreme하지만, 논문의 난도 역시 Extreme 했습니다.
XGBoost Parameter Search
XGBoost / LightGBM / CatBoost와 같이 Boosting 알고리즘의 Variations들은 대개 자신들의 알고리즘을 구현해둔 패키지를 함께 제공하는데, 이들은 논문에서 설명한 개념을 사용하기 위한 파라미터들이 많습니다. 대부분 자동적으로 최적의 파라미터를 default로 설정하기는 하지만, 적어도 패키지를 사용할 때 어떤 파라미터를 어떻게 활용하고 있는지에 대한 고찰이 필요합니다. 따라서 이에 대한 정리도 XGBoost: Parameters에 정리하였습니다.
TREE BOOSTING IN A NUTSHELL
본 장에서는 Gradient Boosting을 간략하게 짚고 넘어가겠습니다. X’GBoost’의 근간이고 사실 XGBoost의 GBoost 부분이 Regularization 부분을 제외하면 비슷하기 때문입니다. 또한 Loss Function에 2차 근사식 또는 Taylor Expansion을 사용하는 부분도 Friedman(GBM 저자)가 제안을 했었던 부분이 있기에 그 근간을 먼저 살펴볼 필요가 있습니다.
Gradient Tree Boosting
기본적인 Gradient Tree Boosting은 다음과 같은 식을 같습니다.
$\hat y_i = \phi(x_i) = \sum_{k=1}^K f_k(x_i), f_k\in F$
여기서 $\phi(x_i)$는 전체 Gradient Boosting 에 $i$번째 instance를 input으로 넣었다는 뜻입니다.
따라서 각 $f(x)$는 개별적인 Base Learner를 뜻할 때, $\sum_{k=1}^{K}f_k(x_i) = f_1(x_i) + f_2(x_i) + … + f_K(x_i)$로서 나타낼 수 있습니다.
Gradient Boosting은 일련의 $f(x)$들 중에서 어떤 $f(x)$를 Add 해나갈지에 대한 고민을 합니다. 그래서 Gradient Boosting을 Additive Model 이라고도 부릅니다.
그럼 새롭게 더할 $f(x)$는 무엇을 근거로 전체 모델에 도움이 되는 함수로 판단하여 더할 수 있을까요? 모든 머신러닝에서 마찬가지로 GBM에서도 Loss Function을 활용합니다. Loss Function을 Minimize하는 방식으로 Optimization을 진행해봅시다.
$L(\phi)=\sum\limits_{i}l(\hat{y_i}, y_i)+\sum\limits_{k}Ω(f_k)$ (2)
전체 Tree 구조인 $\phi$의 Loss function은 위와 같습니다. $\phi$는 Training Loss랑 정규화 Term이 있기에 이들을 설명하겠습니다.
먼저, Training Loss, $\sum\limits_{i}l(\hat{y_i}, y_i)$ 부터 살펴보겠습니다. $i$번째 instance에 대한 예측값과 Label, 또는 정답과의 차이들을 합산한 것입니다. 그리고 Notation에 안 나와있지만 기본적인 가정은 가장 latest인 t 번째 base learner에서 이루어지고 있다는 것입니다. t번째 이전의 Learner들에 대해선 이미 Loss를 구해놨기 때문입니다.
다음으로는 정규화 $\sum\limits_{k} \Omega(f_k)$ 가 존재하며, 이는 각 Base Learner가 지나치게 큰 영향력을 갖지 않게 조절해주는 부분입니다. Tree 같은 경우에는 Node갯수나 트리의 깊이를 조절하거나, Leaf의 Weight에 L2 Norm을 가해주는 식으로 진행됩니다.
Loss Function
$L(\phi) =\sum\limits_{i}^nl(\hat{y_i}, y_i)+\sum\limits_{k}Ω(f_k)$
보통 Loss Function을 구한 다음, Optimization을 하는 과정에서, Euclidean Space를 통해 미분을 하고, Gradient를 계산하여 진행합니다. 하지만 Loss Function의 입력값이 $\phi$인 이상, Numerical Vector가 아니라 Function을 파라미터로 활용하기 때문에 Optimization이 불가능하게 됩니다. 따라서 이를 해결하기 위하여 Boosting이 Additive Training인 점을 활용하여 Optimize가 가능하도록 Loss Function을 변환합니다.
$\phi$ 자체가 Function이기 때문에 미분이 불가능하다는 것이 잘 이해가 안될 수 있습니다. 이는 간단하게 $\phi$가 뜻하는 바가, “함수들을 더하는 함수”라고 생각하고, (함수의 연산자)라고 생각을 한다면 불가능하다는 것을 알수 있습니다.
Additive Training이란 연속적으로 더해지면서 훈련을 진행한다는 뜻이며 다음과 같이 표현할 수 있습니다.
$\hat y_i^0 = 0$
$\hat y_i^1 = f_1(x_i) = \hat y_i^0 + f_1(x_i)$
$\hat y_i^2 = f_1(x_i) + f_2(x_i)= \hat y_i^1 + f_2(x_i)$ …
$\hat y_i^t = \sum_{k=1}^t f_k(x_i) = \hat y_i^{t-1} + f_t(x_i)$
해당 Notation을 $L(\phi)$에 적용하게 되면,
$L^{(t)} = l(y_i, y_i^{(t-1)} + f_t(x_i))+ \Omega(f_t)$
$L^{(t)} = l(y_i, y_i^{t-1} + f_t(x_i)) + \Omega(f_t)$와 같이 적을 수 있습니다.
$\Rightarrow$ (해석): Loss function $L^{(t)}$ 는
- [정답 $y_i$] 와
- [$t-1$ 시점의 예측값 $y_{i}^{(t-1)}$ 에, 현재 시점 $t$ 의 tree를 통해 예측한 $f_t(x_i)$ 를 더한 값] 의 Loss에
- 정규화 부분 $Ω(f_t)$ 를 최소화 해야합니다.
이 Loss Function을 미분 가능한 식으로 전환하기 위하여, Taylor Expansion의 2차 근사식을 적용합니다. 적용하는 절차는 다음과 같습니다.

$L(t) \simeq [l(y_i,y^{(t−1)})+g_if_t(x_i)+\frac{1}{2}h_if_t(x_i)]+\Omega (f_t)$
해당 식에서 $\Omega(f_t) = \gamma T + \frac{1}{2}\lambda\sum\limits_{j=1}^{T}w_{j}^2$ 와 $l(y_i, \hat y_i^{(t-1)})$는 Constant이므로 삭제해주면,
$\tilde{L}^{(t)} = \sum\limits_{i=1}^{n}[g_if_t(x_i) + \frac{1}{2}h_if_{t}^{2}(x_i)] + \gamma T + \frac{1}{2}\lambda\sum\limits_{j=1}^{T}w_{j}^2$ 와 같은 식을 얻을 수 있게 됩니다.
이제 정규화 표현식까지 원래 식으로 치환해서 나열하게 되면, 문제가 발생합니다. 앞의 부분은 $\sum\limits_{i=1}^{n}$ , $i$ 에서 $n$ 까지를 나타내며, 정규화 부분은 $\sum\limits_{j=1}^{T}$, $j$에서 $T$ 까지이므로 목적식을 간단하게 만들고 통일하기 위해선 둘 중에 하나의 $\sum$ 으로 통일해줘야 합니다. $\sum\limits_{j=1}^T$ 로 통일해보겠습니다.
$=\sum\limits_{j=1}^{T}[(\sum\limits_{i\in I_j}g_i)w_j + \frac{1}{2}(\sum\limits_{i\in I_j}h_i + \lambda)w_{j}^2] + \gamma T$
-
$(\sum\limits_{i\in I_j}g_i)$ = $j$ 번째 leaf에 포함된 instance set($I_j$)의 1차 미분 값들의 합 > $G_j$로 치환
-
$(\sum\limits_{i\in I_j}h_i)$ =$j$ 번째 leaf에 포함된 instance set($I_j$)의 2차 미분 값들의 합 > $H_j$로 치환
$=\sum\limits_{j=1}^{T}[G_jw_j + \frac{1}{2}(H_j + \lambda)w_{j}^2] + \gamma T$로 최종 목적식을 구성할 수 있게 되며, 따라서 해당 목적식을 최소로 만드는 $w_j$를 미분식 =0으로 찾게 된다면,
$G_jx + \frac{1}{2}(H_j + \lambda)x^2 = 0$ 으로 나타나고, Leaf의 Weight를 나타내는 $w_j = -\frac{G_j}{H_j+\lambda}$로 표현할 수 있게 됩니다. 그리고 Optimal한 Tree에 대한 Score는 해당 $w_j$를 목적식에 넣은 값으로 정리하자면,
-
$w_j = -\frac{G_j}{H_j+\lambda}$
-
Objective Function = $-\sum_{j=1}^T [\frac{G_j^2}{H_j+\lambda}] + \gamma T$ = Structure Score of Tree q 로 구성할 수 있습니다.
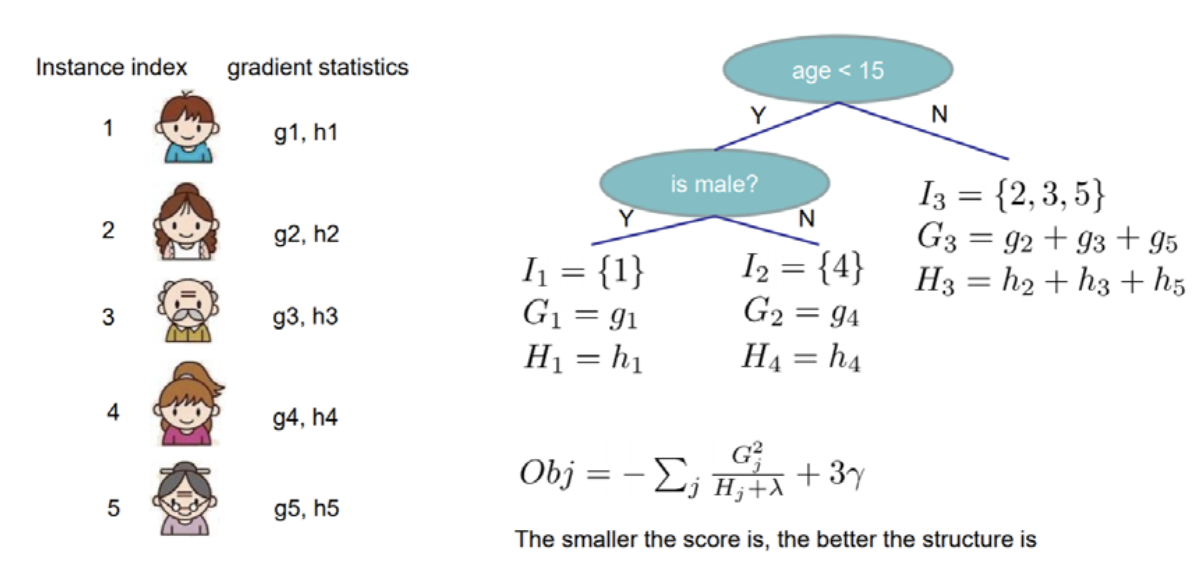
위의 그림은 논문에서 사용하는 그림인데, “Smaller the score is, the better the structure is”라고 하는데 결국 $w_j$가 음수이므로 절대값이 커질수록 값은 작아지고, 이에 따라 Loss도 작아지게 되니, Tree Structure Score가 점점 좋아진다고 할 수 있겠습니다. 즉, -$[\frac{G_j^2}{H_j+\lambda}]$ 값이 높아지면, 트리의 Loss가 감소하게 될 것이니, 해당 값을 통해 Tree가 잘 수립되었는지 살펴볼 수 있게 되는 것입니다.
저희의 최초의 목적은 최적의 $\phi$를 찾아냄에 있어 미분이 불가능했던 부분이었습니다. 이에 따라, Boosting이 Additive Training인 점, 테일러 2차 근사와 각종 대입을 통해 미분이 가능하게 되었고, 그 미분을 통해내어 구해는 값은 결국,
$L^{(t)} = l(y_i, y_i^{(t−1)} + f_t(x_i)) + \Omega (f_t)$에서 $f_t(x_i)$ 인 추가되는 Tree에 대한 최적의 Node Weight와 Tree Structure Score가 되게 됩니다.
즉, 이를 통해 XGBoost에서 활용하는 CART 알고리즘의 Tree Node Weight의 최적값을 찾고, 해당 Weight로 Node들을 구성하고 트리를 구성했을 때의 트리 점수를 얻게 되어 최적화가 가능해지게 됩니다.
그리고 잊지 말아야 하는 점은 $w_j = -\frac{G_j}{H_j+\lambda}$ 값이 하나의 노드에 대한 값이라는 점입니다. 즉, 이제 최적의 Split을 판단함에 있어서,
$L_{split} = \frac{1}{2}[\frac{(\sum_{i \in I_L}g_i)^2}{\sum_{i\in I_L}h_i + \lambda} + \frac{(\sum_{i \in I_R}g_i)^2}{\sum_{i\in I_R}h_i + \lambda} - \frac{(\sum_{i \in I}g_i)^2}{\sum_{i\in I}h_i + \lambda}] - \gamma$ 를 활용할 것인데, 이 때 각 원소들이 Left, Right, Center의 Node의 값이며, 마치 Decision Tree를 구성할 때와 식이 유사해지는 것을 볼 수가 있습니다. 해당 $L_{split}$은 분할을 진행했을 때의 감소폭을 나타내는데, 감소폭이 큰 분할을 선택하는 쪽으로 Split을 진행합니다.
SPLIT FINDING ALGORITHMS
Basic Exact Greedy Algorithm
저희는 이제 Tree를 분할하는 ‘기준’에 대해서 알게 되었습니다. 그러면 해당 기준을 토대로 어떻게 최적의 분할을 낳을 수 있는 지 알아보겠습니다.
가장 Basic하고 정확한 방법은 모든 경우의 수를 다 시도해보고 그 중 최고의 성능을 보이는 것을 최선이라고 여기는 것입니다. 하지만 데이터가 너무 크면 계산이 매우 힘들어 질 것입니다. 이를 위해서 보완할 수 있는 방법은 미리 Feature를 Sorting하는 방법입니다.
예를 들어, [33,25,87, 45,9, 13, 2, 44]의 Feature가 있다고 해보겠습니다. 이 Feature의 최적의 Split을 찾아보기 위해선 모든 데이터를 기준으로 분할을 해보아야 합니다.
먼저 33을 기준으로 한다면 나머지 데이터를 돌며, 33보다 작은 사람 거수 / 33보다 큰 사람 거수 를 외치며 돌아다녀야 합니다.
하지만 데이터가 좌우로 정렬을 제대로 하고 있다면 어떻게 될까요? 그렇다면 맨 왼쪽의 데이터를 분할점으로 잡으면 우측에 있는 데이터는 무조건 분할점보다 크므로 분할을 쉽고 빠르게 진행할 수 있습니다.
Approximate Greedy Algorithm
앞에서 언급한 것처럼, Basic Exact Greedy Algorithm은 모든 가능한 탐색을 전부 돌기 때문에 당연히 최적해를 찾기에 용이합니다. 하지만 데이터가 매우 크다면 Computation의 비용과 시간이 지나치게 많이 들고, memory에 데이터가 들어가지 못해 빠른 계산이 불가능할 것입니다.
이에 논문에서는 Approximate Framework를 제시합니다.
Approximate Framework, 또는 Approximate Greedy Algorithm은 말 그대로 모든 탐색을 하는 대신, 근사를 하겠다는 것입니다. 이를 위해 Sorting한 Feature 분포의 백분위수, Percentile들을 구하고 그것들을 Candidate Splitting Points(후보 분할 지점)으로 지정합니다. 그 이후, 분할 지점을 통해 데이터를 나누어 Bucket으로 묶고, 각 Bucket의 $g_i$, $h_i$와 같은 통계량을 계산하여 그것을 기반으로 최선의 분할을 정합니다.
이 부분에 대하여, 제가 [오해를 했던 부분]과 [이해를 했던 부분]을 설명드리겠습니다. 오해를 했다가 점하나를 빼서 이해를 하게 되었습니다…
[오해를 했던 부분]
처음에 저는 Percentile을 통해 Split을 할 때, Binary Split을 진행한다고 생각했습니다. 따라서, 다음과 같이 Split을 하고 통계량을 구해 Best Split을 정한다고 생각했습니다.
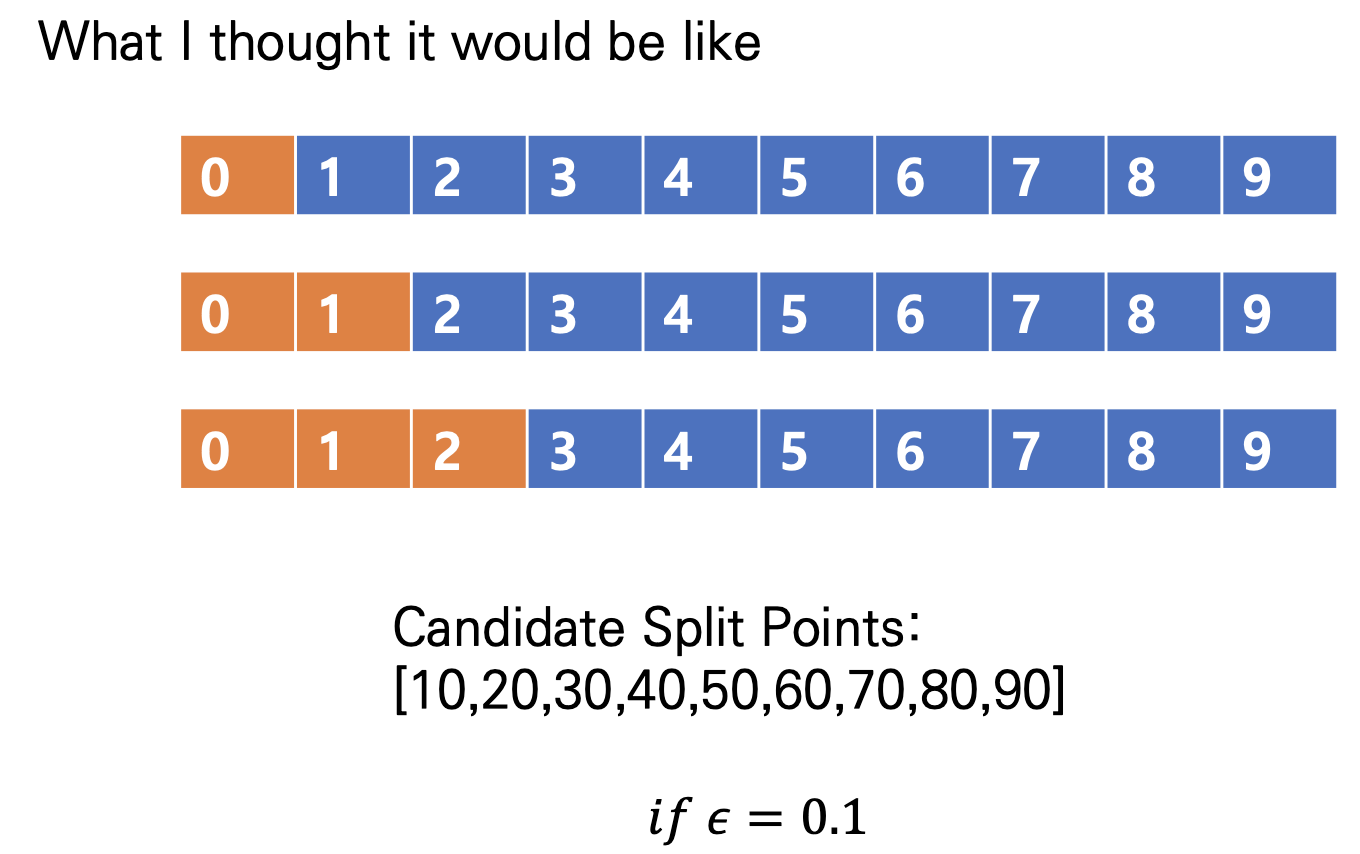
하지만 다음과 같이 정의하게 되면, Node가 두개밖에 나타나지 않으므로, Bucket이 두개밖에 존재할 수 없습니다. 이는 굳이 Bucket이라는 새로운 개념을 정의할 필요가 없으며, 연산의 큰 변화도 없게 됩니다. 중간 노드에서 Left와 Right Node로 나눈다는 점에서 차이가 없기 때문입니다.
[이해를 했던 부분]
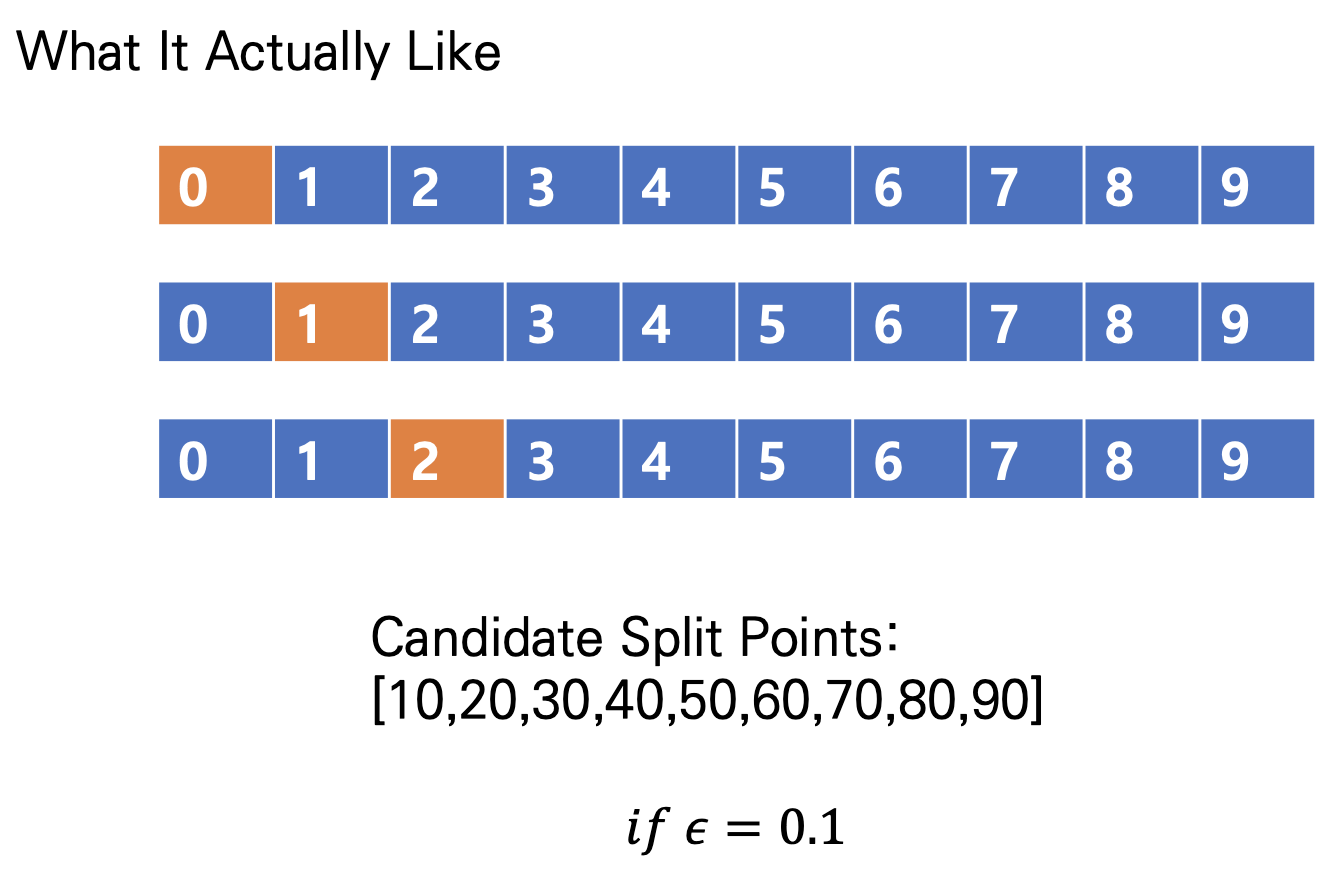
따라서 Approximate Greedy Algorithm를 다시 정의하자면 위의 그림과 같습니다. Percentile을 통해 각 Bucket을 나누어 그 Bucket 내부에서 Split을 진행하여, 도출되는 $g_j, h_j$를 합쳐서, 가장 큰 값이 나오는 Bucket을 기준으로 분할하게 되면 최적의 Split을 구할 수 있게됩니다. 이 부분에 대하여 명확해 진 계기는 알고리즘 Pseudo Code를 보고 알게 되었습니다.
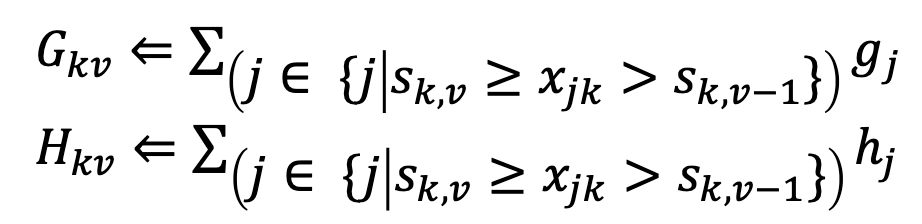
위의 식과 같이 하나의 Feature k에 대하여, $v-1, v$ 사이의 값을 대상으로 통계량을 구하는 것을 볼 수 있습니다. 이는 첫번째 그림으로는 달성할 수 없고, Bucket을 사용하는 두번째 그림으로 설명할 수 있습니다.
하지만 이에 대하여 확실히 강필성 교수님의 극단적인 예시가 좀 더 이해하기 쉽기 때문에 해당 예시를 사용해보겠습니다.
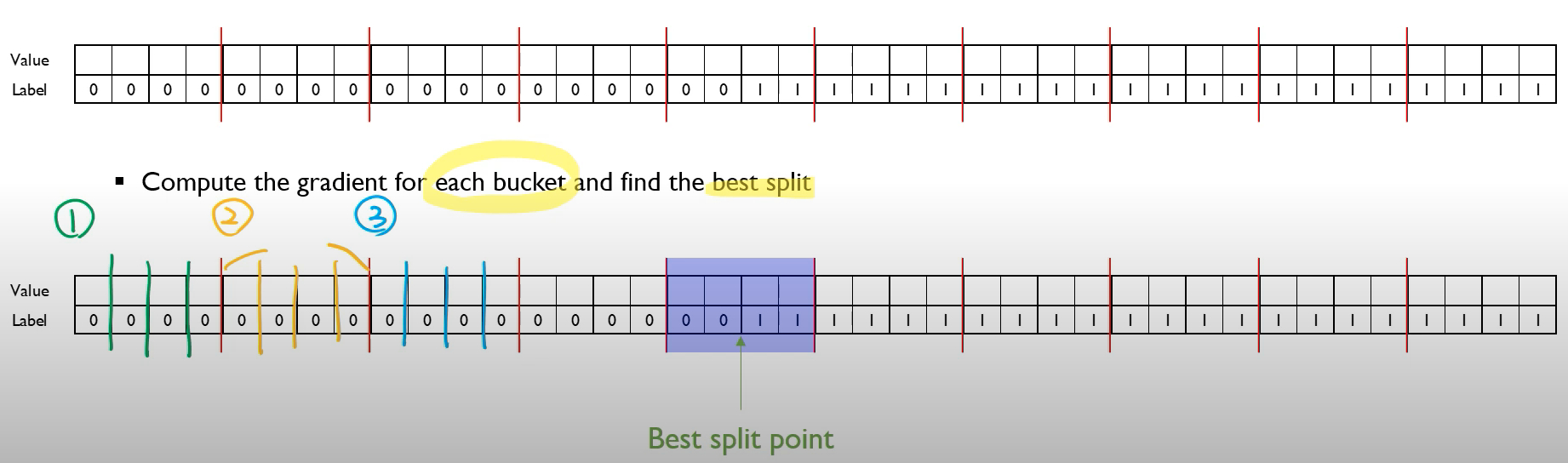
해당 예시에서는
- Quantile을 통해 Bucket Split을 정한 뒤 (빨간선)
- Bucket 내부에서 Split을 일일이 진행하고 해당 통계량을 합산
- (보라색 음영)에서, Label 0,1이 공존하게 되는데 해당 Bucket에서 분할을 했을 때, 최적의 Split임을 알 수 있습니다.
이때 Approximate Greedy Algorithm에서도 Global, Local의 두 가지 버전으로 나뉘게 됩니다.
Global Variant & Local Variant
Global Variant는 트리를 구성하기 시작할 때 분할의 후보를 모두 계산해 놓고, 모든 단계의 Split에서 같은 후보를 사용합니다. 이에 반해 Local Variant는 실제 Split이 진행될 때 분할의 후보를 계산합니다. 즉, 모든 단계의 Split이 달라지게 됩니다.
이는 예시를 통해 살펴보겠습니다.
100개의 Feature과 100개의 원소를 갖고 있는 데이터가 있다고 합니다. 이 때, 10분위수의 Global 과 Local Variant의 움직임을 살펴보겠습니다.
Global은 미리 100개의 Feature에 대하여 Sorting을 진행한 후, 각 Feature에 대한 10분위수를 구해둘 것입니다. 따라서, 100개의 Split 묶음 100개가 나타나 $10^5$개의 Split 후보가 존재할 것입니다.
Local은 Split이 일어나는 곳에서만 후보를 구하기 때문에 만약 Split이 두번 일어나게 된다면, 2개의 Column만 사용할 것이니, 2번의 후보 탐색을 통해 100 * 2 = 200개의 Split 후보군을 구하게 될 것입니다.
둘의 차이점을 명시하자면, 확실히 Global Variant는 후보 탐색 횟수가 적어서 편해보일 수 있습니다. 하지만 Local에서는 매 Split이 일어날 때마다 계산이 되니 분할이 이루어진 데이터에 대해 분할 후보를 계산할 것이므로 Global로 구한 Split보다 깊은 트리에 어울리게 됩니다. 그리고 후보 탐색 역시 위에서 예시로 보인것과 같이 ‘대개’ Global이 후보가 더 많을 것입니다.
아래는 Global & Local Variant / $\epsilon$에 대하여 정리한 그림입니다.

Weighted Quantile Sketch
솔직히 말씀드리자면, 해당 Sketch 섹션은 완벽한 이해를 하지 못했습니다. 하지만 Sketch에 대한 저의 스케치를 말씀드리자면 다음과 같습니다.
Sketch는 별도의 알고리즘입니다. 이는 Sample Data로 Sketch를 하여 Original Data Distribution을 파악한다는 것인데, 이는 Approximate Greedy Algorithm이 하고자 하는 바입니다. 명확하게는 Quantile Sketch Algorithm으로서 Quantile의 Sketchfhtj Original Data Distribution을 확인하는 것입니다.
하지만 XGBoost에서는 Weighted Quantile을 사용합니다.
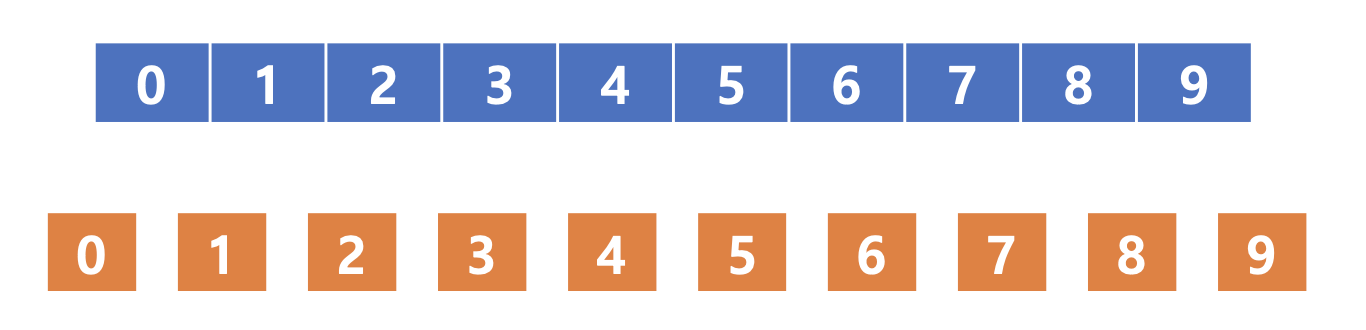
다음과 같이 Quantile을 통한 Bucket이 있을 때, Quantile을 정한 기준은 Feature Value를 Sorting 했을 때의 Value의 Quantile이었습니다. 따라서 1~100의 값이 주어졌을 때의 Quantile은 10,20,…90이 되는 것입니다. 이에 Weighted Quantile은 각 Quantile에서 나타나는 통계량이 같아지는 Quantile을 정하고자 합니다. 원래 Quantile은 Feature의 크기를 통해 분할하기 때문에 통계량의 값이 차이가 날 수 있으나, Weighted Quantile을 사용하게 되면, 모든 Bucket의 통계량이 일정하게 나타나게 될 수 있습니다.
이때 통계량이라 함은, $g_i, h_i$가 아니라 $h$만을 뜻합니다. $h$인 2차 미분, 또는 헤시안은 Gradient의 미분입니다. 그런데 Gradient는 방향으로서, 해당 방향으로 이동하면 Optimum으로 다가갈 수 있다는 뜻입니다. 즉, 그 방향을 미분했다는 뜻은 Optimum에 닿을 수 있다, 못한다를 판단해주는 값인데 이 의미를 통계량으로 활용한다고 합니다.

이것이 어떤 장점을 갖는지, 그리고 제가 설명한 것이 옳은 지에 대해선 확신은 없습니다. 확실히 이 부분에 대해선 참고 자료가 많이 부족했기 때문입니다. 하지만 최대한 조사 후에 설명해본 바입니다.
Sparsity-aware Split Finding

XGBoost는 논문 제목에서도 나타나 있듯이, Scalability를 매우 강조합니다. 따라서, 광범위하게 어떤 데이터를 마주하더라도 최적의 성능을 보이고자 하는 노력, 즉 Generalization이 많이 반영이 되어 있습니다. 본 단락에서는 현실의 데이터가 대부분 Sparse하다는 것을 염두한 XGBoost의 모습을 살펴보겠습니다.
현실의 데이터가 Sparse할 수 있는 대표적인 이유는 3가지이며, 이런 Sparsity를 항상 염두를 하여 데이터를 다루어야 합니다.
- 데이터에 Missing Value가 있는 경우
- 다수의 0의 값을 갖는 경우
- One-hot encoding과 같은 기법의 영향
Sparsity를 해소하기 위해, XGBoost는 각 tree의 노드에서 위와 같은 현상을 겪는 데이터에 대하여 ‘Default Direction’, 즉 기본 방향을 설정해줍니다. 즉, 데이터가 Missing인 경우 해당 instance는 기본 방향으로 흘러갑니다. CART의 같은 경우는 트리의 분할 방향이 2개 밖에 없으므로, 왼쪽/오른쪽 중 하나의 길을 배정받게 될 것입니다.
Sparsity-aware Split Finding 알고리즘을 한 줄 씩 이해하기 전에, 간단하게 정리하면 다음과 같습니다. 마치, 우등생이 하는데로 공부하면 성적이 자동적으로 오를꺼다 라는 정신을 담은 것 같습니다.
기존의 Non-Missing Data가 가는 길로 Missing Data를 보내자!

Sparsity-aware Split Finding 알고리즘 절차
- Initialization
Initialization에서는 다음과 같은 목록을 설정합니다.
- $I$: 현재 노드의 instance set
- $I_k = {i \in I | x_{ik} \neq missing }$ : k feature의 Missing이 아닌 instance set
- $d$ = Feature dimension
- $G \Leftarrow \sum_{i\in I}g_i, H \Leftarrow \sum_{i\in I}h_i$ 현재 instance set의 Gradient(1차 미분) / Hessian(2차 미분)
- Iteration
feature k =1 부터 끝까지 iteration을 진행합니다.
//enumerate missing value goto right
결측치를 모두 오른쪽 노드로 이동하게 합니다. 그 후, 해당 Split의 점수를 계산합니다
//enumerate missing value goto left
결측치를 모두 왼쪽 노드로 이동하게 합니다. 그 후, 해당 Split의 점수를 계산합니다
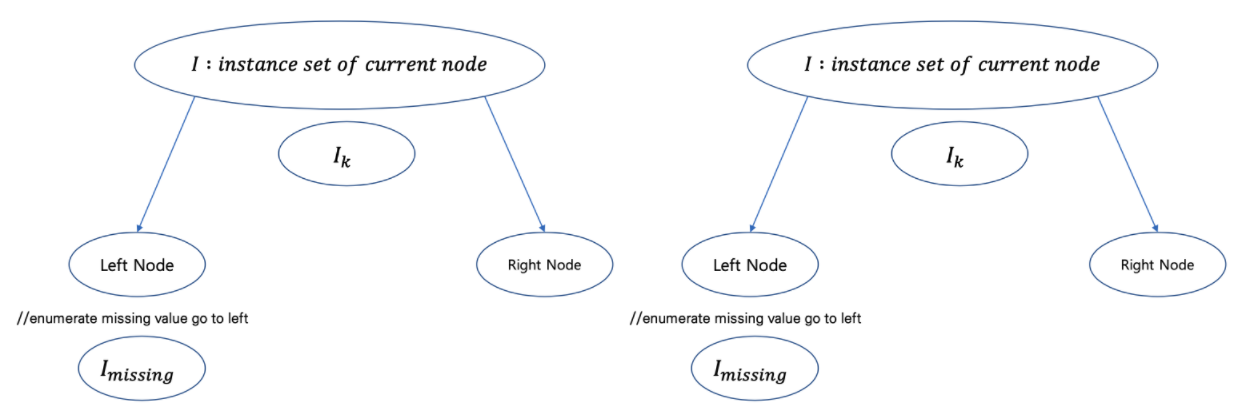
score를 매번 계산하는데 max를 계속 덮어 써서 Left로 보냈을 때 score가 높은지, Right로 보냈을 때 score가 높은 지 비교하여 높은 쪽으로 Default Direction을 선정합니다.
알고리즘이 뭔가 복잡해보이는데 하나씩 대입 / 비교를 통해 이해할 수 있었습니다. 아무리 긴 알고리즘이라도 애송이 같은 마인드가 아닌 장군의 마인드로 정복해나가는 연습을 해나가야 할 것 같습니다.
논문 발표 당시, Tree Learning을 사용하는 알고리즘은 대부분 Sparsity 문제를 사전에 해소한 Dense data에 적용하거나 별도의 해소방법을 사용했습니다. 하지만 XGBoost는 단일한 방법 (기본 방향으로 Missing Data를 전부 보내는 방법)을 사용하여, Computation과 처리 방법의 간단함을 선사하게 됩니다.
SYSTEM DESIGN
Column Block for Parallel Learning
사실 위의 Approximate Greedy Algorithm을 설명할 때, 소개했던 Block은 논문의 해당 개념을 설명할 때는 등장하지 않고, System Design 섹션에 와서 설명합니다. 즉, 알고리즘을 설명한다음 그것을 가능케하는 시스템 디자인을 설명하는데, 이 부분에서 XGBoost의 알고리즘적 제안은 단순히 시스템적 디자인이 가능하도록 구성하는 것이라는 점을 깨닫게 되었습니다.
위에서 Block이란 결국, 데이터를 하나의 Column을 기준으로 정렬했을 때, Quantile에 해당하는 Block이라고 설명했습니다. 이렇게 Block 단위의 계산은 결국 Parallelization이 가능하게 되어 연산의 혁신을 불러오게 됩니다.
또한 Block 내에서 데이터들은 Compressed Column Storage(CSC) 형태로 저장되게됩니다. 이는 단순하게 그림으로 살펴보시면, 아래와 같으며, 마치 Sparsity Aware Split Finding에서 제안한것처럼 결측치 부분을 한 쪽으로 치우는 것과 같습니다.
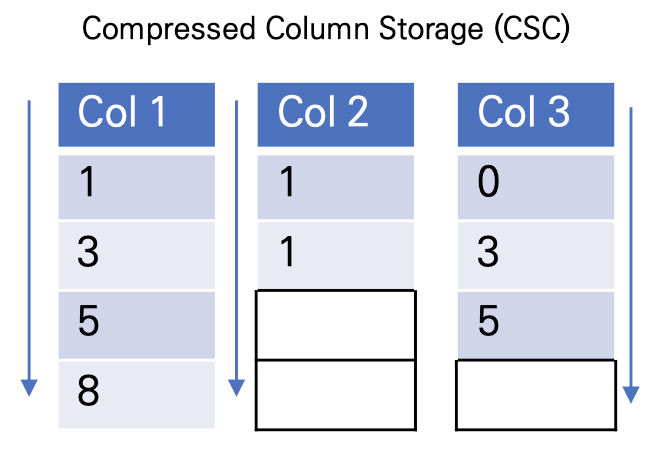
논문에서 언급하지는 않지만, 위와 같은 꼴로 CSC를 구성함으로써, 데이터의 양도 줄이고, Sparsity Aware Split Finding를 위한 시스템 디자인을 만든것이라고 생각합니다.
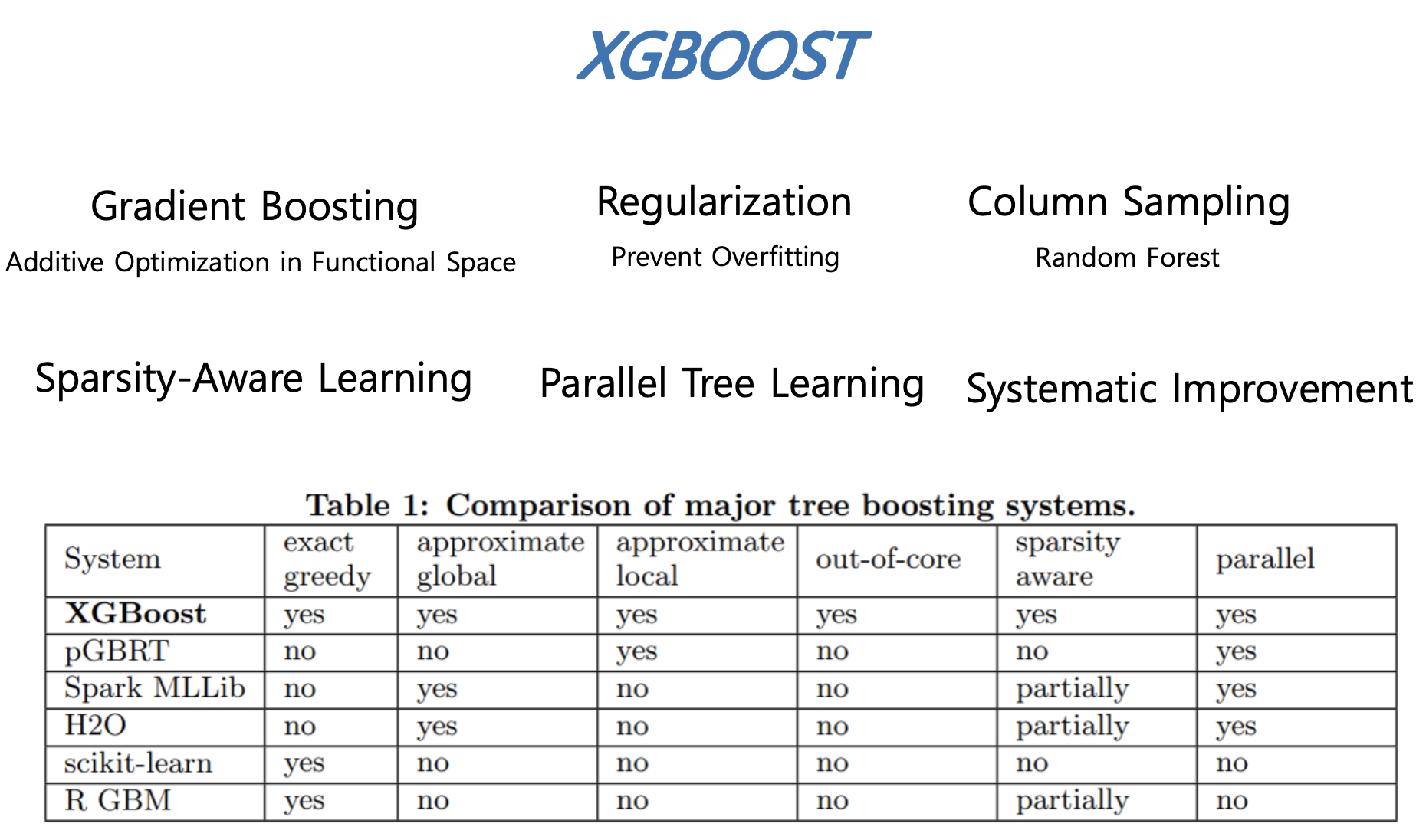
RELATED WORKS
다음 그림은 XGBoost가 포함하고 있는 장점 및 특징을 정리한 것이며, 다른 모델들과의 비교표입니다.
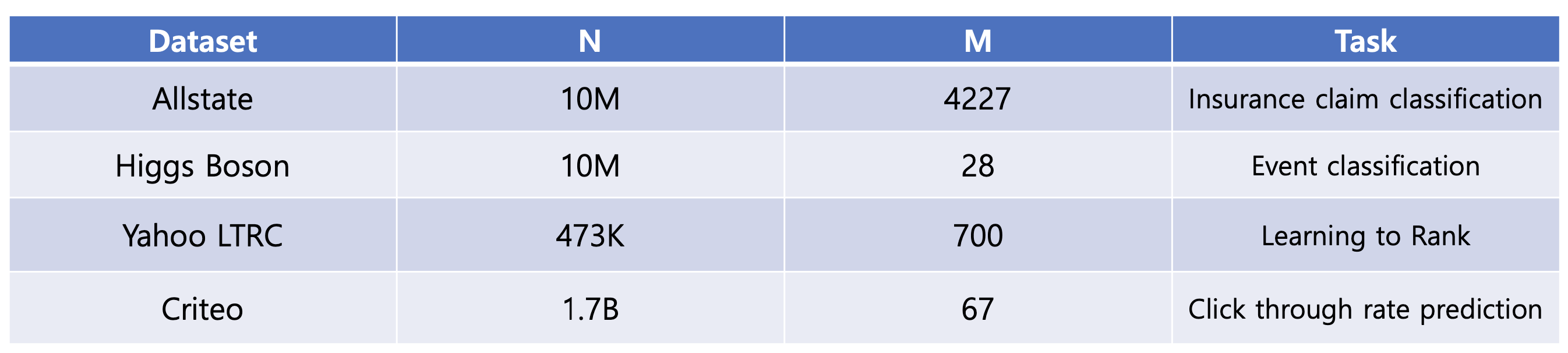
END TO END EVALUATIONS
저자들은 XGBoost에 대한 실험을 여럿 진행했습니다. 이 때, 아래의 데이터 셋을 통해 실험했습니다.
Classification
XGBoost는 Regression, Ranking 에도 사용이 되지만 본 포스트에선 분류 문제에 대한 성능만 살펴보면 다음과 같습니다.
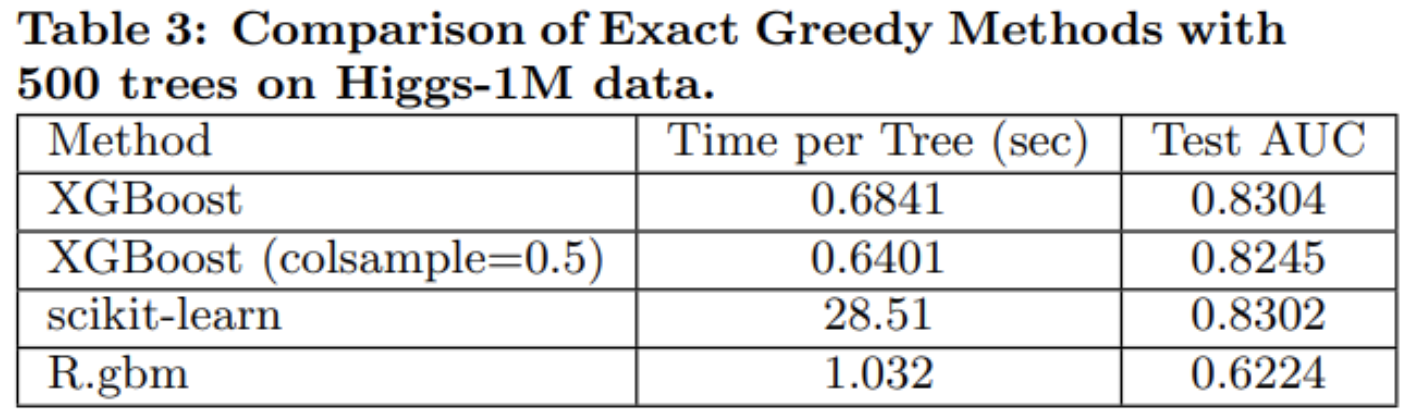
Scikit-learn은 어떤 알고리즘을 사용한지 정확하게 파악하지 못했으나, GBM일 것이라고 판단되며, R에서 제공하는 GBM, XGBoost의 성능을 비교한 표입니다. 즉, 성능과 시간 모두 XGBoost가 압도적으로 좋은 것을 볼 수가 있습니다. 물론 Scikit-learn하고의 성능차이는 크지 않으나, 속도면에서는 차이가 매우 큽니다.
논문 감상평
- XGBoost의 알고리즘 개선은 컴퓨팅적 개선을 하기 위한 초석일 뿐입니다.
- 컴퓨터에 대한 원리를 이해해야 좀 더 자세한 이해를 할 수 있습니다.
- 사용한 Boosting이 이름이 XGBoost이지만, 엄밀하게 따지면 Newton Boosting이라고 할 수 있습니다. 하지만 놀랍게도 이에 대한 언급이 없습니다.