Algorithms for Hyper-Parameter Optimization

**James Bergstra, Remi Bardenet, Yoshua Bengio, Balazs Kegl (2011) **

본 포스트는 고려대학교 산업경영공학과 강필성 교수님의 Business Analytics 논문 구현 과제의 일환으로 작성되었으며, 3장 Anomaly Detection의 Parzen Window 관련 논문입니다. Anomaly Detection이 3장의 주제이지만, 학부생 시절 Parzen Window를 통해 Hyperparameter Search를 진행해본적이 있고, 그에 대한 개념을 정확하게 알지 못하여, 이번 기회에 해결해보고자 하는 취지로 진행하였습니다.

Grid vs Random Search

본 논문은 HyperParameter(HP) 탐색에 대한 논문입니다. 즉, 논문의 주제가, 분석의 주 목표인 성능 향상을 위한 모델 구성보다는 부차적인 느낌이 들지만 오히려 같은 모델을 사용하더라도 HP에 따라 성능이 달라지기에 오히려 중요한 역할을 한다고 생각합니다.

보통 HP를 Optimize할 때 보편적으로 많이 사용하는 방식은 다음의 세가지 방법입니다. 본 논문에서 소개하는 모델 기반의 HP 최적화보다 훨씬 더 직관적이며 쉽기 때문에 많이 사용합니다.

Manual Search: 한땀한땀 연구자가 어떤 파라미터가 성능 향상에 좋을 지 살펴보고 비교한다.
Grid Search: 파라미터의 Grid를 설정하고 범위 내의 모든 파라미터 조합을 사용하여 비교한다.
Random Search: 파라미터의 Grid를 설정하지만 범위 내의 Random 조합을 사용하여 비교한다.

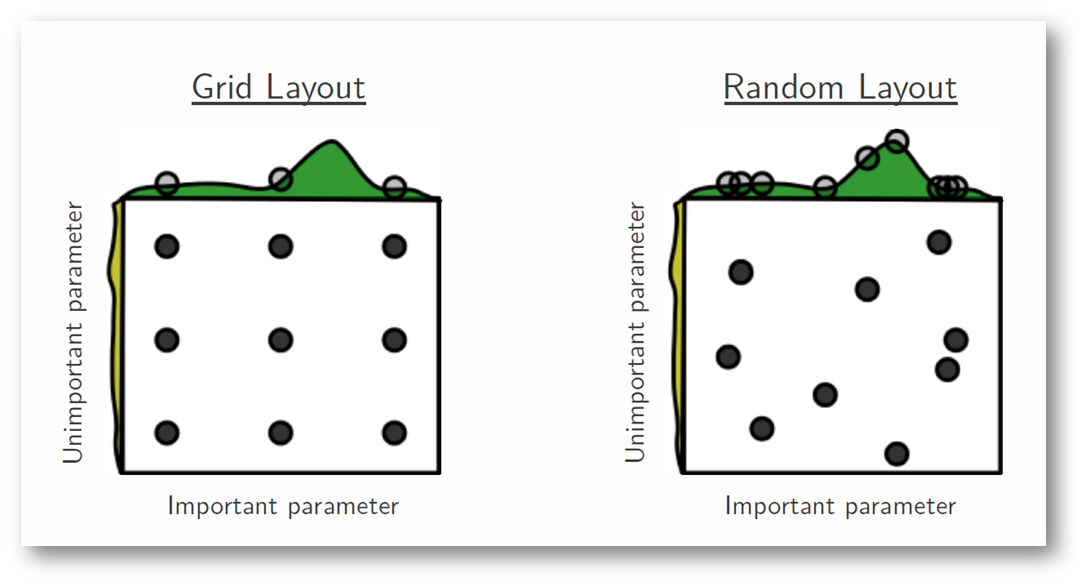
여기서 재밌는 특징은 Grid Search보다 Random Search가 HP를 탐색할 때 더 적은 탐색 횟수로도 좋은 성능을 가져온다는 것입니다. 본 논문의 같은 저자가 본 논문 발표 다음 해에 낸 논문인데, 간략히 원인을 설명하겠습니다.

위의 그림과 같이 하나의 중요한 파라미터와 덜 중요한 파라미터가 있고, 이에 대한 HP를 탐색한다고 해보겠습니다. Grid Search 같은 경우에는 중요 파라미터의 3개의 지점을 살펴볼 수 있지만, Random Search는 9개의 Distinct한 지점에 대하여 모두 살펴볼 수 있어, 최적 파라미터를 발견할 수 있는 가능성이 높아지게 되는 것입니다.

하지만 이 세가지 방법들은 확실히 시간이 많이 걸리고, 그에 따른 컴퓨팅 자원도 많이 소모하게 됩니다. Grid Search를 대표적으로 예를 들면, 10개의 HP가 각기 (1,100)의 range의 후보를 갖고 있다면, $100^{10}$의 탐색을 진행해야 하며, 이에 대한 비용은 매우 클 것입니다. Random도 결국 범위가 주어지고 해당 범위 내에서 마구잡이로 탐색하기에, 횟수가 정해진다 했을 때, 정확한 탐색이 불가능할 수 있습니다.

따라서, 수많은 후보를 모두 탐색해서 정하는 방법(Grid) 또는 마구잡이 선택(Random)보다 특정한 기준을 가진 모델을 통해, 파라미터를 탐색해나가는 방식이 필요합니다. 이는 마치 Manual Search를 하지만, 사람이 직접하는 것이 아닌, 통계적인 모델을 통해 탐색해나가는 방식과 같습니다. 맨 처음 HP를 선택한 다음 다음에는 어떤 HP를 적용해야 성능이 향상될 지에 대한 “방향”을 안다면, 굳이 많은 횟수로, 또는 마구잡이로 탐색을 할 필요가 없습니다. 그것이 바로 “Sequential Model-based Global Optimization(SMBO)”이며, 이름을 풀면 다음과 같습니다.

Sequential하게 Model에 기반하여 지엽적이지 않은, 전체 파라미터 공간에 대한 탐색을 한다

Sequential Model-based Global Optimization(SMBO)

SMBO는 다음으로 시도해볼만한 파라미터 조합에 대하여 나름의 “근거”를 갖고 Optimization을 진행하는 기법입니다. 이에 대한 이해는 두 가지 개념을 수반하며, 다음과 같습니다.

Surrogate Model
Acquisition Function

Surrogate Model

브루스 윌리스가 등장하는 “Surrogate”라는 영화를 아시나요? 세상의 모든 사람들의 바깥 세상의 위험을 감수하기 싫어, 대신 집 안에서 자신과 닮은 로봇을 조종하여 외부의 생활을 이어나가는 내용의 영화입니다. 이와 같이 Surrogate, 대리인이라는 이름을 가진 모델은, 원래의 목적식이 계산이 복잡하여, 반복적으로 시행하기에는 힘들 때 대신 사용하는 모델이라고 합니다.

Surrogate Model을 통해 최적화를 위해 어떤 방향으로 파라미터 조합을 이동시켜야 최적의 HP값을 얻을 수 있을 지에 대한 판단을 하게 됩니다. 저는 위의 표현이 다소 아쉬웠던 것이, 예를 들어, 어떤 모델의 Loss에 대한 목적 함수가 존재할 때, 이를 아예 대체해버리는 것이 Surrogate Model 이라고 생각했습니다. 하지만 절차를 따라가다 보면, 완전히 대체하는 것은 아니며, Objective Function의 관측값이 Surrogate Model의 관측값이 되며, Surrogate Model은 Objective Function의 관측되지 않은 값들이 어떻게 이루어져 있을까에 대한 대강의 구조를 생성해주는 역할을 합니다. Surrogate Model을 통해 Objective Function에 대한 이해가 간단하게라도 가능하면, 시도 해볼만한 파라미터를 추정할 수 있는 것이지요.

SMBO의 Pseudo Code는 다음과 같습니다.

$f, M_0, T, S:$ 각기 원래 모델, 최초의 Surrogate Model, SMBO 시행 횟수, Surrogate Model의 다음 탐색 파라미터 추천 시스템(Acquisition Function)
$H$는 처음에는 공집합으로서, Surrogate Model이 제안하는 파라미터와 그에 대한 Objective Function Return 값입니다.
횟수 $T$만큼,
Surrogate Model 다음 파라미터 추천 시스템에서 최소로 나오는 값을 $x^*$로 잡고
해당 $x^*$를 원래 Objective Function에 넣어 값을 구합니다. 이 부분이 Surrogate Model이 완전하게 원래의 Objective Function을 대체하는 것은 아니라고 설명한 부분입니다.
추천 $x^{}$ 와 $f(x^{})$ 를 $H$에 포함시키고, Surrogate Model을 Update합니다. Surrogate Model은 지속적으로 업데이트 되는데 이는 Prior가 관측값을 통해 Posterior로 변하는 절차와 같습니다.

Acquisition Function

위에서 Surrogate Model이 탐색해야 하는 다음 파라미터를 추천해주는 시스템이라 하여 추천 시스템이라고 언급한 것이 바로 Acquisition Function입니다. 이에 대한 식은 다음과 같습니다.

$EI_{y^}:= \int_{-\infty}^{\infty}max(y^ - y, 0)p_M(y|x)dy$

Acquisition Function의 종류로는 Probability of Improvement 또는 Expected Improvement 등이 있지만, 본 논문에서는 후자인 EI를 사용하여 논리를 풀어나갑니다.

위의 $EI$를 Minimize할 때의 식을 읽어보면,

$P_M(y|x)$: Surrogate Model은 확률 분포로 구성되기 때문에 $x$일 때, $y$의 값을 나타냅니다.
$max(y^{}-y,0)$ 가 0보다 크게 되면 $y^$ 보다 $y$ 가 작은 것이므로 이 때의 $x$ 가 다음 파라미터로 추천되는 것입니다.
$y^*$는 기존의 파라미터로 구한 $y$ 값 중 최소의 값을 나타낸 것입니다.

본 논문의 주요 Contribution은 원래 Objective Function을 근사하는 Surrogate Model을 제안한 것이며 이는 Gaussian Process와 Tree-structured Parzen estimator입니다. 두 과정 모두 분포에 기인한 것이므로 $EI$에서 확률분포를 사용한 것이 이어지게 됩니다.

Surrogate Model (1) - Gaussian Process

Gaussian Process(GP)는 정말 어렵습니다. 카이스트의 문일철 교수님께서 해당 개념 하나만을 정리한 영상이 15개 이상이며, 이해 및 응용이 매우 난해합니다. 하지만 최대한 쉽게 설명을 시작해보겠습니다…

GP의 가장 기본적인 아이디어는 $y = f(x)$로 함수 $f$에 $x$ 입력값을 넣었을 때 나타나는 $y$가 단순하게 하나의 값이 아닌 $\sigma$를 표준편차로 갖는 분포의 평균값이라는 것입니다. 그리고 보통 머신러닝, 딥러닝에서 $f(x)$의 $x$는 단일한 값이 아닌 벡터로서 나타나기 때문에, $x$ 벡터 $[x_1, x_2, …, x_k]$에 대하여 각기의 변수가 평균과 분산을 갖는 Multivariate Gaussian Distribution으로 나타나기에 평균 벡터와 공분산 벡터를 갖게 됩니다.

GP를 이해하기 위하여 많은 자료를 탐색했으며, 시각적으로 가장 잘 표현한 포스트를 참고하여 설명해보겠습니다.

$f$의 $x$를 2차원 벡터로 두고, 이에 대한 Multivariate Gaussian Distribution을 그려보면 다음과 같습니다. 그리고 이를 고차원 데이터를 표현할 때 사용하는 Parallel Coordinates로 표현하면 우측 그림과 같습니다.

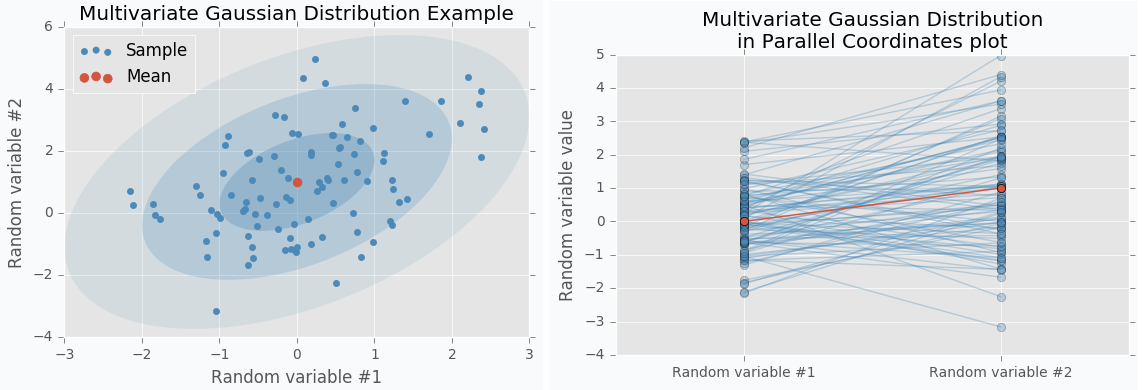
지금은 2차원의 분포를 표현한 것이지만, 만약 $x$의 차원이 증가한다면 어떻게 될까요? 3차원까지는 Gaussian Distribution을 표현할 수 있겠지만, 그 이상을 나타낼 수 없으며, 이를 보이기 위해선 Parallel Coordinates를 사용해야 합니다.

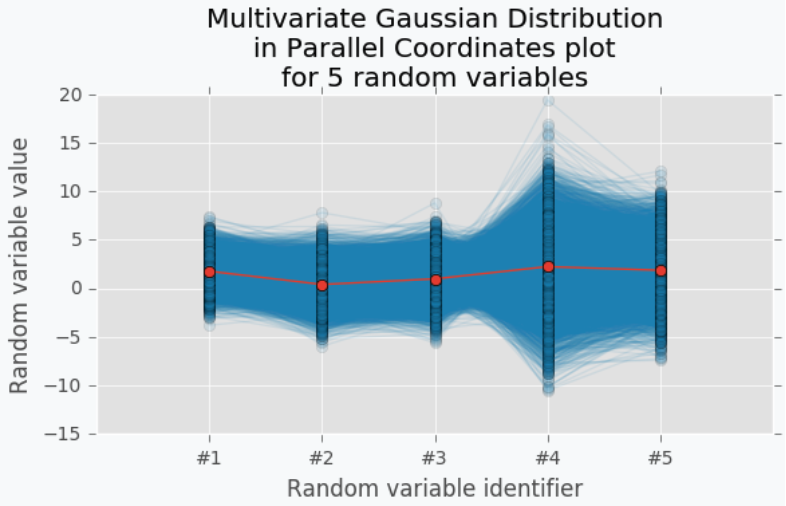
5차원의 Gaussian Distribution에 대한 평균을 이은 점이 빨간색 선이 되겠으며, 나머지 데이터가 파란색으로 나타나게 됩니다. 이렇게 살펴보면 빨간색 선은 결국 하나의 선으로 표현되면서 Function으로서 나타나지게 됩니다. 평균들을 이어서 하나의 함수로 나타내는 것을 GP의 Surrogate Function으로 간주하며 해당 Function에서 최댓값을 갖는 지점의 $x$를 찾아 다음으로 시도해볼 만한 파라미터로 제시합니다. Surrogate Model에서 최대값을 갖는 파라미터가 원래 모델에 적용했을 때도 최대 값을 산출해 낼 수 있을 것이라 생각하기 때문입니다.

사실 위의 빨간색 점으로 이은 것은 GP에 대한 설명이지만, HP를 업데이터 하기 위해서는 단일 변수에 대한 예시를 들어보겠습니다. Random Variable이 여러개가 아니라 하나의 파라미터에 Range가 $x$축으로 나타나고 표현하는 surrogate model을 살펴봐야 하기 때문입니다.

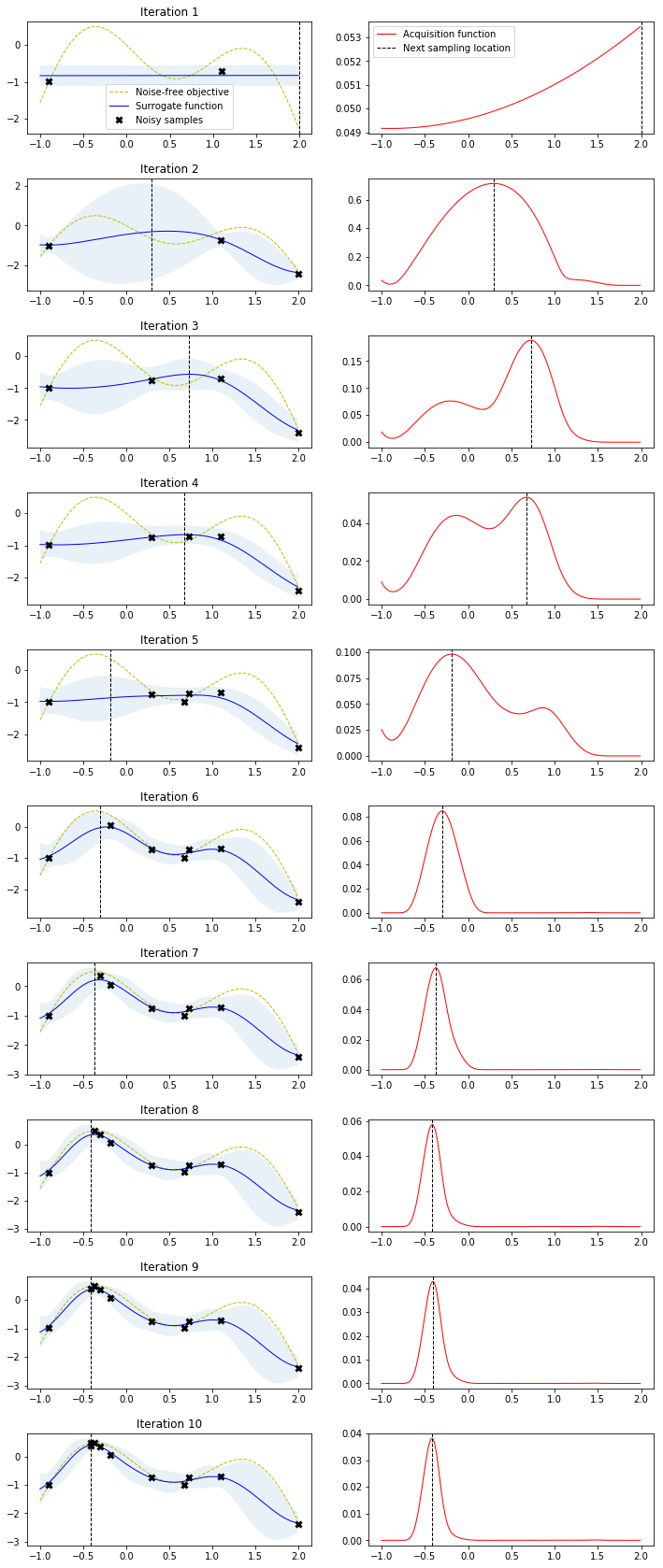
그림이 다소 크지만 이해를 위해서 어쩔 수 없이 가져온 그림입니다. GP의 첫번째 Iteration을 시작하여 관측값 두개로 시작한다고 해보겠습니다. 관측된 지점은 확실한 $y$값이 있으므로, 분산이 존재하지 않지만, 그 사이에 대해서는 모르는 영역이므로 두 점을 있는 Mean들의 Non-Linear Regression속에서 분산을 갖습니다. 2번째 Iteration을 보시면 최대값의 $x$를 구하는 것을 볼 수 있으며, 그것이 평균을 나타내는 파란선과는 다른 것을 볼 수 있습니다. Surrogate Model은 Approximation일 뿐이기에 실제값과 약간 상이할 수 있기에 나타나는 현상이며, 실제 값을 다시 Surrogate Model에 적용하여 Update해주게 됩니다. 이런 식으로,

Surrogate Model 내의 최대의 $y$값에 대한 $x$를 구하고,
이를 원래의 Objective Function이 넣어 값을 구하고 Surrogate Model을 Update해줍니다.
정해진 Iteration만큼 반복합니다.

여기까지만 보면 이해가 어렵지 않습니다. 하지만 다른 포스트들에서의 그림을 살펴보면 약간 다른 의견을 제시하여 혼란을 야기합니다.

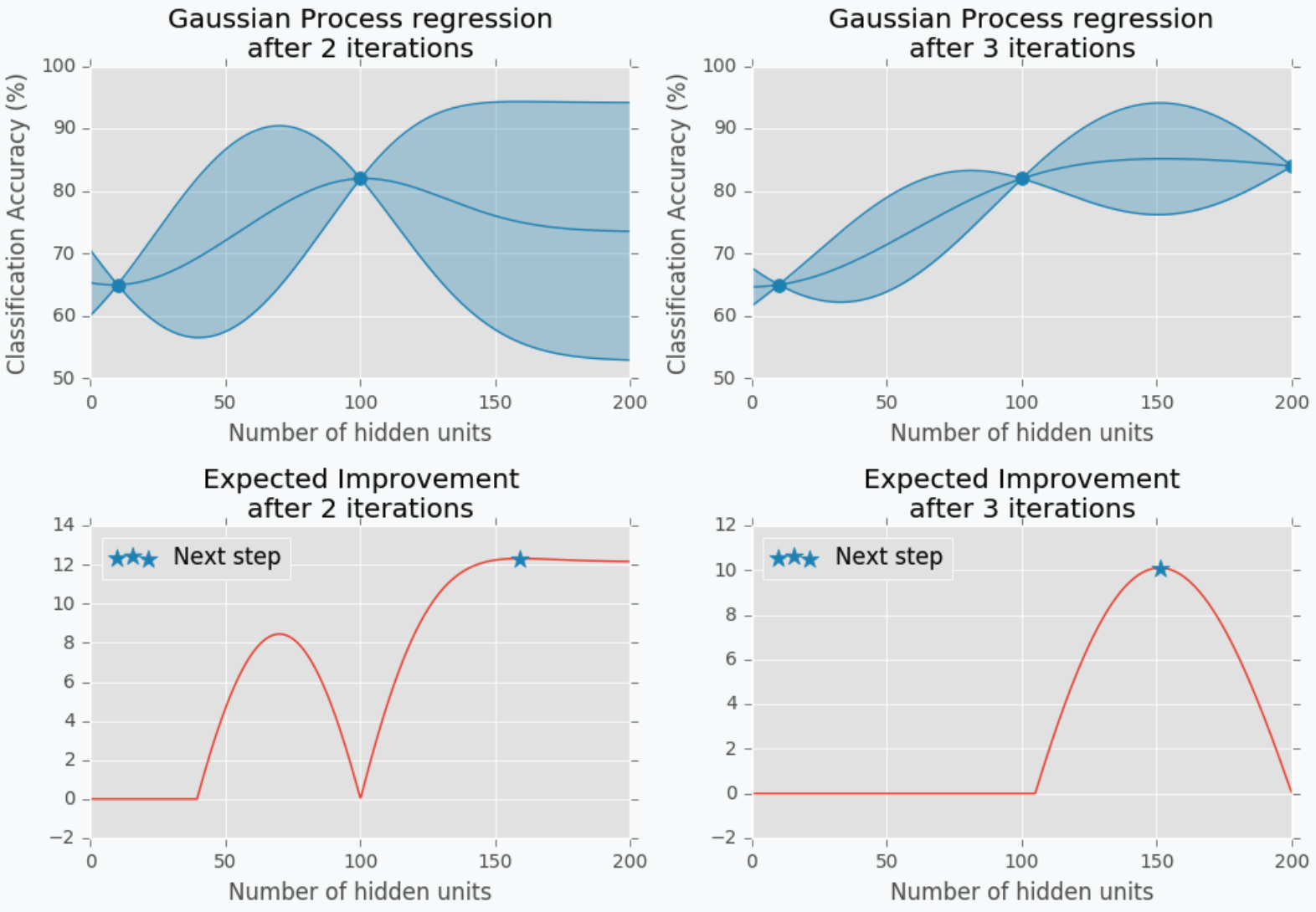
어느 부분에서 혼란이 오시는가요? 위에서는 Surrogate의 Maximum value의 $x$를 다음 파라미터로 추천해준다고 했습니다. 그런데 위의 그림에서 2번째 iteration의 과정을 살펴보면 Maximum은 $x$가 100인 지점인데 다음 step으로 지정해주는 곳은 150 근처입니다.

이렇게 다른 추천이 나타나는 이유는 EI를 산정하는 방식이 두가지로 나뉘기 때문입니다.

Exploration (탐험): 분산이 제일 큰 지점을 추천한다.
Exploitation (착취): Surrogate Model의 최대값을 추천한다.

Iteration 10을 표현했던 위의 그림이 Exploitation만을 사용하여 그림을 표현한 것으로 추측됩니다. 그 이유는 -0.5부근에서 local optimum이 발생하여 못 벗어나고 있기 때문입니다. 하지만 위와 같이 이미 Surrogate Model 내에서 최대값이 나타나버리는 경우에는 더 이상 그것을 넘는 경우가 없는데 왜 새로운 값을 탐색하려 할까를 생각해야 합니다. 저희가 사용하고 있는 Surrogate Model은 어디까지나 Approximation이기에 항상 더 좋은 파라미터가 없을 지 경계해야합니다. 따라서 똑같은 지역만 착취하듯이 계속 탐색하는 것 보다는 좋은 결과가 나타날지, 안나타날 지에 대한 판단이 안 서도 ‘탐험’을 통해 분산이 큰 곳으로 뛰어드는 Exploration까지 한다면, Local Optimum에 빠지지 않을 수 있습니다.

Surrogate Model (2) - Tree-structured Parzen Estimator Approach

TPE도 역시 매 HP 탐색의 매 iteration마다 어떤 조합으로 시도를 할 지에 대한 추천을 해줍니다. 하지만 크게 두 부분에서 차이점이 발생합니다.

Expectation Improvement 식의 차이
사용하는 분포의 차이: GP = Gaussian / TPE = Parzen Window Density (KDE)

TPE의 절차는 다음과 같습니다.

Random Search를 통해 파라미터를 선정하고 그에 대한 $y$값을 구하여 초기 Surrogate Model을 구합니다.
Surrogate Model에 대하여 특정값보다 작은 그룹과 큰 그룹으로 나눕니다. 이는 하이퍼 파라미터로 설정하며, 0.2일 경우에는 큰 그룹 80% / 작은 그룹 20%로 나눕니다.
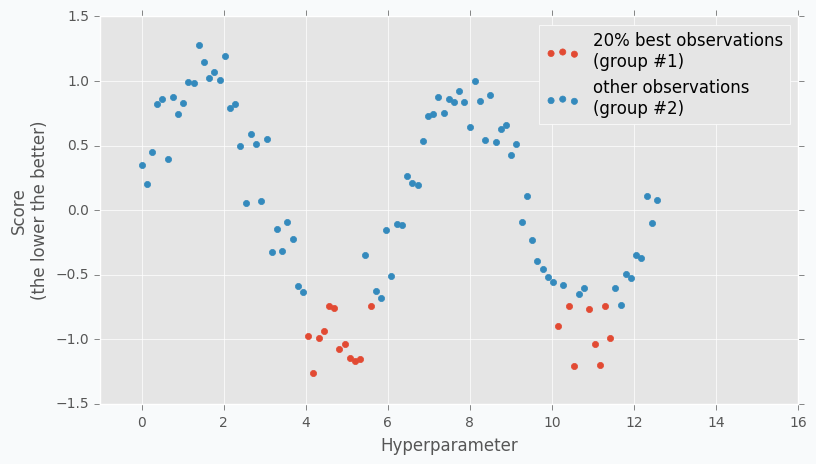
해당 $x$ 그룹들에 대하여 분포를 생성하며 작은 그룹 (우수)을 $l(x)$, 큰 그룹 (열등)을 $g(x)$라고 표기했을 때, Expected Improvement는, 우수한 그룹의 분포내에서의 확률이 열등한 그룹 내에서의 확률보다 높은 정도가 큰 지점으로 나타나게 됩니다. 아래의 그림에서는 분포를 t-분포로 나타냈는데, 확실히 우수한 그룹의 확률이 열등한 그룹에서의 확률보다 높은 지점이 다음 추천 파라미터로 사용됩니다.

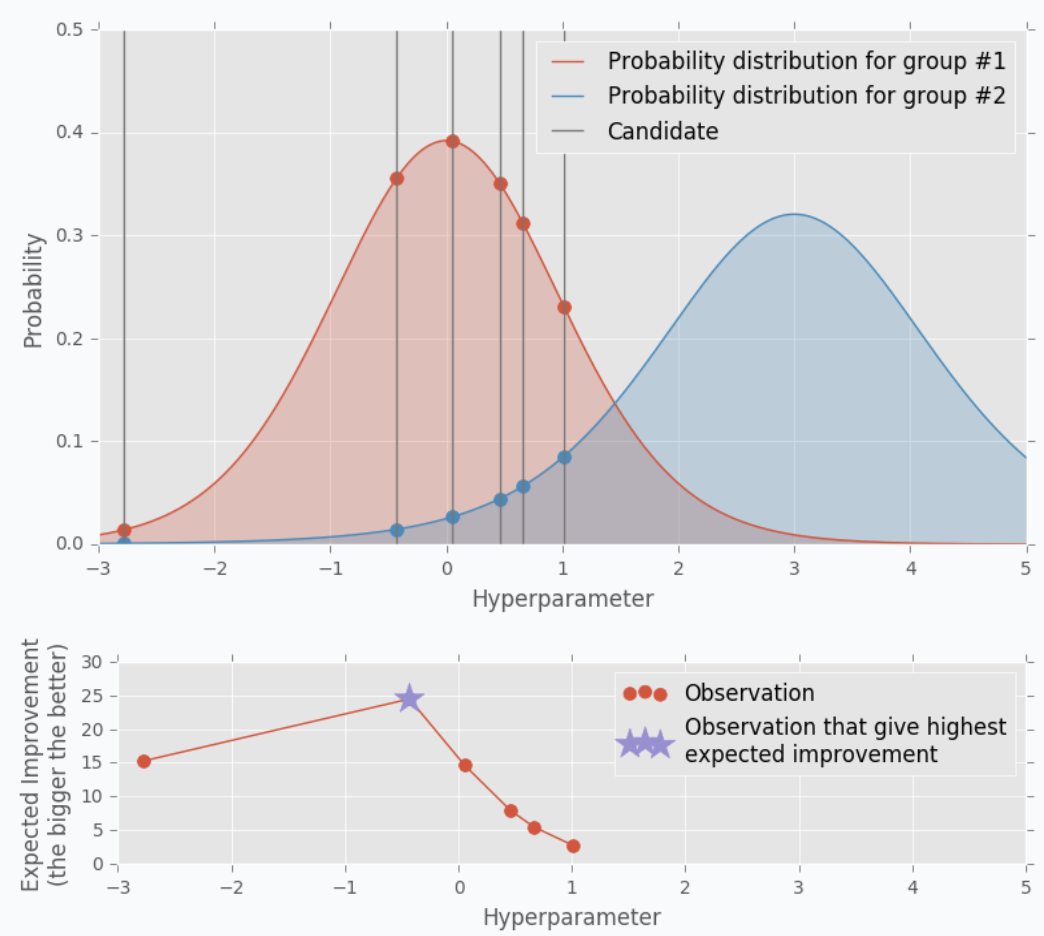
즉, $EI$는 다음과 같은 식으로 나타납니다. $EI(x) = \frac {l(x)} {g(x)}$

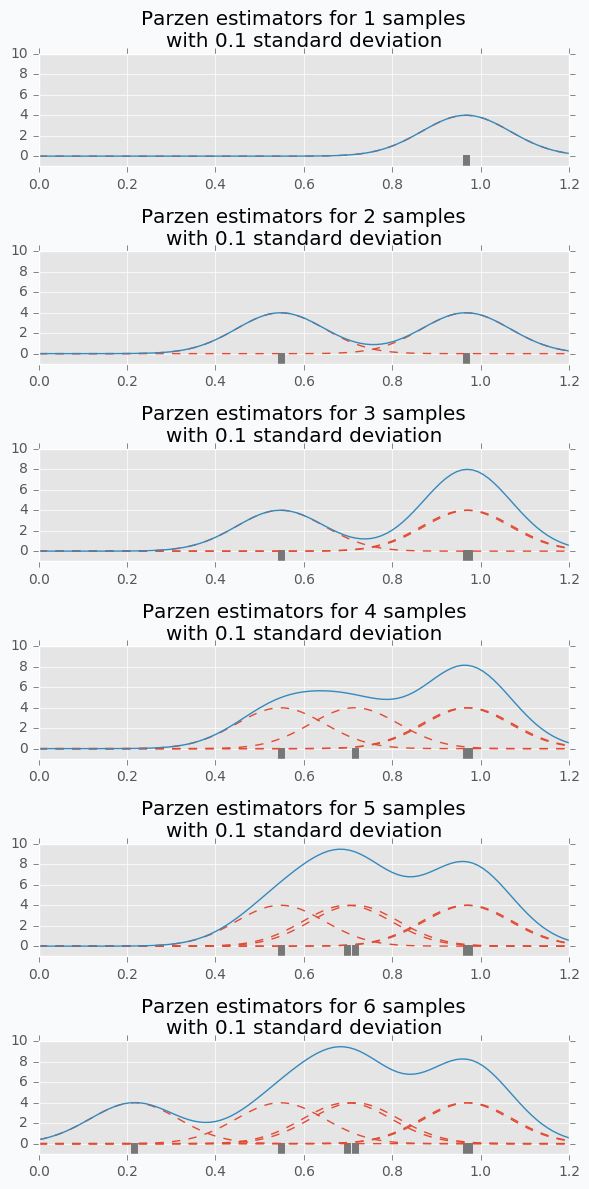
$EI$의 차이에 더불어 분포의 사용도 다릅니다. GP에서는 각 $x$에 대한 $y$의 분포가 Gaussian으로 나타나, 평균과 분산을 통해 하나의 Function, 즉 Surrogate Model을 구성하는 것을 살펴보았습니다. 하지만 TPE에서는 Parzen Window Density를 구성하여, 그 분포내에서의 확률을 살펴봅니다. 간단하게 Parzen Window Density를 설명하자면, 매 데이터들을 Gaussian의 평균으로 가정한 분포를 지속적으로 겹쳐서 하나의 Mixture Modeld를 구성하는 것입니다. 따라서, 위와 같이 말끔한 분포가 나타나기보다는 어린왕자의 모자마냥 울퉁불퉁한 분포가 나타나게 됩니다.

GP / TPE 코드 구현

논문에서는 Random Search보다 자신들이 제안하는 SMBO가 더 우수하다는 것을 보이기 위해 같은 조건으로 성능 비교를 진행합니다.

데이터 셋: Boston Housing dataset (Regression) Input Variables: 13개 / label: House Price / 데이터 갯수: 506
Training Algorithm: Multi Layer Perceptron, Deep Belief Network(본 포스트에서는 다루지 않음)
Hyperparameters: 10개 / 하지만 논문에서 대표적으로 표기하는 파라미터는
- Learning Rate
- L1 / L2 정규화
- Hidden Layer 갯수
- Iteration 횟수
로 나타납니다. 하지만 실험의 간단함을 위하여 Hidden Layer 하나만으로 비교하고자 합니다.

정리하자면, 구현에 있어 GP / TPE를 사용한 SMBO를 Grid Search와 비교하여 과연 성능이 더 좋은지에 대한 확인을 해보는 시간을 가져보겠습니다. SMBO는 Bayesian Optimization이기에 이에 관련하여 유명한 패키지인 BayesOpt 또는 HyperOpt를 사용해도 되지만, 저자가 직접 구현했다는 hyperopt를 사용해서 구현해보고자 합니다. 그리고 Training Algorithm인 MLP를 구현함에는 Pytorch를 사용했습니다.

Boston Dataset Load

Boston Dataset을 Pytorch의 Dataset을 통해 불러오고, 그것을 배치 단위로 사용할 수 있도록, DataLoader를 사용해 구성합니다.

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

class Boston_Dataset(Dataset):
    def __init__(self, train=True):
        boston = load_boston()
        boston_df = pd.DataFrame(boston['data'] )
        boston_df.columns = boston['feature_names']
        boston_df['PRICE']= boston['target']
        X = boston_df.iloc[:,0:13]
        y = boston_df['PRICE']

        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

        if train:
            self.x_data = X_train
            self.y_data = y_train
        else:
            self.x_data = X_test
            self.y_data = y_test

    def __len__(self):
        return len(self.x_data)

    def __getitem__(self, idx):
        return torch.tensor(self.x_data.iloc[idx]), torch.tensor(self.y_data.iloc[idx])

boston_traindataset = Boston_Dataset(train=True)
boston_testdataset = Boston_Dataset(train=False)

boston_trainloader = DataLoader(boston_traindataset, batch_size=5, shuffle=True, num_workers=4)
boston_testloader = DataLoader(boston_testdataset, batch_size=5, shuffle=True, num_workers=4)

MLP Model

MLP Model을 구성하는 것과 함께, Model을 훈련시키는 과정과 Return Value를 사용한 HyperParameter와 그에 대한 성능을 내뱉을 수 있는 Function도 따로 구성을 해야합니다. 그래야 그것들을 다시 SMBO의 Input으로서 넣어 HP에 대한 탐색을 할 수 있기 때문입니다. 따라서 MLP를 Net Class로 구성하고 해당 MLP를 통해 훈련을 진행하고 Test Result를 return하는 Function을 train_network로서 만들겠습니다.

#Create the model
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

class Net(torch.nn.Module):
    def __init__(self, n_feature = 13, size_hidden = 1, n_output=1):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, size_hidden)   # hidden layer
        self.predict = torch.nn.Linear(size_hidden, n_output)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

size_hidden = 10
net = Net(size_hidden)

#Adam is a specific flavor of gradient decent which is typically better
optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate)
criterion = torch.nn.MSELoss(size_average=False)  # this is for regression mean squared loss

def train_network(hidden):
    net = Net(size_hidden = hidden)
    optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate)
    criterion = torch.nn.MSELoss(size_average=False)  # this is for regression mean squared loss
    net.train()
    running_loss = 0.0
    for epoch in range(50):
        for idx, (inputs, labels) in enumerate(boston_trainloader):        
            # zero the parameter gradients
            optimizer.zero_grad()
            # forward + backward + optimize
            outputs = net(inputs.float())

            loss = criterion(outputs, torch.unsqueeze(labels.float(),dim=1))
            loss.backward()
            optimizer.step()

            # print statistics
            running_loss += loss.item()
#         if epoch % 10 == 0:
#             print('Epoch {}'.format(epoch+1), "loss: ",running_loss)
        running_loss = 0.0

    net.eval()
    test_loss = 0
    for idx, (inputs, labels) in enumerate(boston_testloader):
        outputs = net(inputs.float())
        loss = criterion(outputs, torch.unsqueeze(labels.float(),dim=1))
        test_loss += loss.item()
    avg_test_loss = test_loss / len(boston_testloader)
    return avg_test_loss

Surrogate Model - GP

그 다음으로는, GP를 구현합니다. SMBO를 진행하기위하여 필요한, Surrogate Model을 Gaussian Process로 구성하고, 다음 파라미터 추천을 EI로 나타내고, 그것을 통해 HP를 선택합니다.

import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C

def vector_2d(array):
    return np.array(array).reshape((-1, 1))

def gaussian_process(x_train, y_train, x_test):
    x_train = vector_2d(x_train)
    y_train = vector_2d(y_train)
    x_test = vector_2d(x_test)

    # Train gaussian process
    kernel = C(1.0, (1e-3, 1e3)) * RBF(10, (1e-2, 1e2))
    gp = GaussianProcessRegressor(kernel, n_restarts_optimizer=100)
    gp.fit(x_train, y_train)

    # Get mean and standard deviation for each possible
    # number of hidden units
    y_mean, y_std = gp.predict(x_test, return_std=True)
    y_std = y_std.reshape((-1, 1))

    return y_mean, y_std

def next_parameter_by_ei(y_min, y_mean, y_std, x_choices):
    # Calculate expected improvement from 95% confidence interval
    expected_improvement = y_min - (y_mean - 1.96 * y_std)
    expected_improvement[expected_improvement < 0] = 0

    max_index = expected_improvement.argmax()
    # Select next choice
    next_parameter = x_choices[max_index]

    return next_parameter

import random

def hyperparam_selection(func, n_hidden_range, data, n_iter=20):

    scores = []
    parameters = []

    min_n_hidden, max_n_hidden = n_hidden_range
    n_hidden_choices = np.arange(min_n_hidden, max_n_hidden + 1)

    # To be able to perform gaussian process we need to
    # have at least 2 samples.
    n_hidden = random.randint(min_n_hidden, max_n_hidden)
    score = func(n_hidden)

    parameters.append(n_hidden)
    scores.append(score)

    n_hidden = random.randint(min_n_hidden, max_n_hidden)

    for iteration in range(2, n_iter + 1):
        score = func(n_hidden)

        parameters.append(n_hidden)
        scores.append(score)

        y_min = min(scores)
        y_mean, y_std = gaussian_process(parameters, scores,
                                         n_hidden_choices)

        n_hidden = next_parameter_by_ei(y_min, y_mean, y_std,
                                        n_hidden_choices)

        if y_min == 0 or n_hidden in parameters:
            # Lowest expected improvement value have been achieved
            break
        print(f"Current Minimum: {y_min}")
        print(f"Suggested n_hidden: {n_hidden}")

    min_score_index = np.argmin(scores)
    print(f"Suggested Hidden: {parameters[min_score_index]}")
    print(f"Minimum Score: {min(scores)}")
    return parameters, scores

Surrogate Model - TPE

위의 GP는 최대한 from scratch부터 구성을 하려 노력했지만, TPE는 마땅한 방안이 생각이 나지 않아, hyperopt의 도움을 받았습니다. Hyperopt를 사용하게 되면, 데이터셋에 따라 알아서 SMBO 내의 HP를 추천해주기도 하는 등, 위에서 직접 짠 코드보다 훨씬 편하게 작업을 수행할 수 있습니다. 특히 마음에 들었던 부분은 trials라는 부분인데, 이는 자동으로 로그를 찍어줘 일일이 결과를 저장하는 코드를 따로 만들어줄 필요가 없다는 것입니다.

import numpy as np
import hyperopt
from hyperopt import tpe, hp, fmin
from functools import partial

# Object stores all information about each trial.
# Also, it stores information about the best trial.
trials = hyperopt.Trials()

tpes = partial(
    hyperopt.tpe.suggest,
    # Sample 1000 candidate and select candidate that
    # has highest Expected Improvement (EI)
    n_EI_candidates=50,

    # Use 15% of best observations to estimate next
    # set of parameters
    gamma=0.15,

    # First 20 trials are going to be random
    n_startup_jobs=20,
)
# tpes는 부분적으로 tpe.suggest에 변형을 적용하여, Custom으로 실험을 진행하는 것을 보여드린 것입니다. 하지만 저는 단순하게 Default Suggestion을 따라서 HP를 찾았습니다.

tpe_best_params = fmin(
    fn=train_network, # Objective Function to optimize
    trials=trials,
    space= uniform_int('hidden', 50, 500), # Hyperparameter's Search Space
    algo=tpe.suggest,
    max_evals=20 # Number of optimization attempts
)

실험 결과

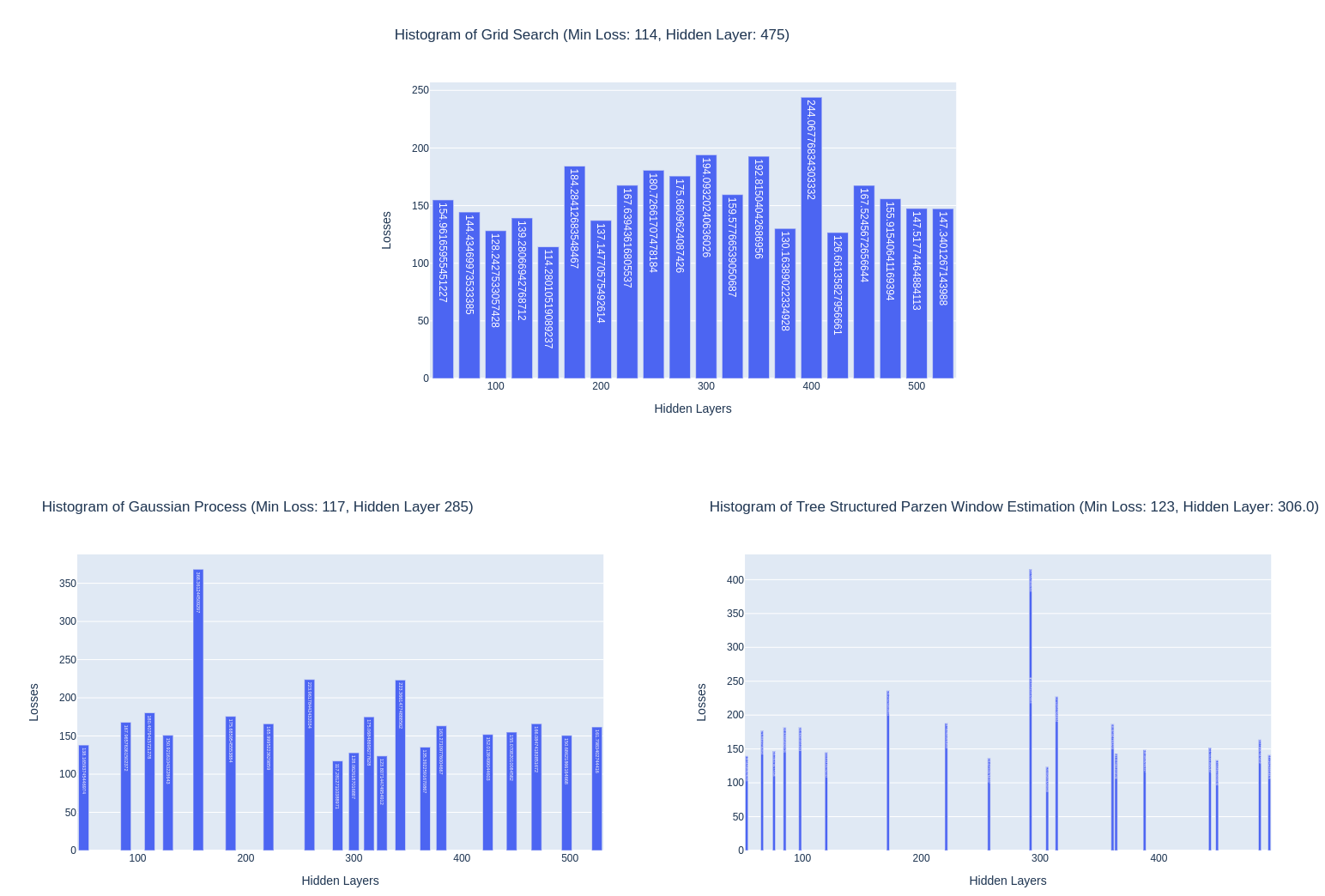
위의 그림은 Grid Search / GP / TPE를 Hidden Layer를 50부터 525까지 설정하고 진행한 결과이며, GridSearch같은 경우는 25 단위로 Hidden Layer를 증가시키면서 탐색, 그리고 나머지 SMBO는 각자의 탐색법으로 진행되었습니다.

지금 위에서 제시한 그래프로는 Grid Search가 최소의 Loss를 찍어내서 의아하겠지만, 매우 운이 좋은 경우이며, 대부분은 SMBO가 더 좋은 성능을 냅니다. 여기서 제가 강조하고 싶은 부분은 바로 그래프의 모양입니다.

GP와 TPE의 그림을 살펴보면, GridSearch와는 다르게 균일하게 Hidden Layer를 탐색하는 것이 아니라, 촘촘한 구역이 있기도 하고 여유로운 공간이 있기도 합니다. 이것이 바로 어떤 파라미터를 사용해야 더 좋은 결과를 얻을 지에 대한 고민을 통해 나타난 결과입니다. 특히 GP의 그림을 살펴보면 X축인 Hidden Layer가 285이 일때 최소의 Loss를 달성했는데, 이에 따라 최대한 그 근처에 파라미터 시도들이 모여있습니다. 즉, 최선의 결과가 나온 곳 주위에서 더 좋은 결과를 기대하고 진행한 것이지요.

Discussion

[성능비교표]

다음은 성능 비교표입니다.다. 한눈에 살펴봐도 TPE > GP > Manual > Random의 순으로 성능이 좋은 것을 볼 수가 있습니다 (에러가 가장 낮은 순). 200번의 trial을 통해 나타난 결과표이며, 이 중 Manual은 사람이 직접 HP를 수정해가면서, 최적의 파라미터를 찾아 나섰는데 convex / MRBI 데이터셋에 대하여 각기 82번 / 27번의 trial을 통해 결과를 나타내었습니다. 저자들은 이를, 성능의 관점에서는 TPE / GP가 좋으며, 효율성의 관점에서는 Manual이 좋지만, 당연히 전자를 사용하는 것이 더 좋다고 합니다.

TPE와 GP는 같은 Surrogate Model로서의 역할을 하는데 왜 TPE가 GP의 성능보다 좋은 결과를 가져올까요?이에 대해 3가지의 원인을 제시합니다.

Perhaps, $p(x|y)$를 통해 $p(y|x)$를 추론하는 것이 직접 $p(y|x)$를 나타내는 것보다 좋을 수 있다.
Perhaps, TPE의 낮은 accuracy로 나타난 exploration이 추론에 오히려 더 좋았을 수 있다.
Perhaps, GP의 exploitation과 exploration의 tradeoff가 효과적이지 않을 수 있다.

라는 식으로 추론만 할 뿐, 구체적인 입증은 하지 않습니다. 하지만 중요한 점은 TPE / GP가 모두 Random / Grid Search의 성능을 상회하기 때문에 둘 사이의 경쟁은 필요 없을 것 같습니다.

Conclusion

본 논문은 SMBO로 HP를 찾아나가는 과정 두 가지를 설명했으며, 사람이나 brute-force random search의 성능을 뛰어넘는것을 보여줬습니다. 또한 Model에 기반한 탐색이기 때문에 탐색 결과에 대한 신뢰성과 성능을 모두 보장받을 수 있으며, 논문 저자들은 이번 논문을 계기로 다소 간과했던 HP 탐색에 대한 중요성을 사람들이 알아줬으면 좋겠다는 마음이 있다고 합니다.