본 포스트는 Medium의 Gamma distribution에 대한 포스트를 번역한 것입니다. https://towardsdatascience.com/gamma-distribution-intuition-derivation-and-examples-55f407423840

감마 분포의 두 파라미터인 $\alpha$, $\beta$ 를 넣기 전에 잠시 몇 질문에 대하여 생각해보자.

애초에 왜 감마 분포를 만들었는가?
(왜 이 분포가 존재하는가?)
모델링에서 감마 분포가 언제 사용되어야 하는가?

1. 왜 감마 분포를 만들었는가?

Answer: 미래의 발생되는 events에 대한 대기 시간을 예측 흠… 근데 그거는 사실 지수분포의 역할이 아닌가? 그럼 지수분포와 감마분포의 차이점은 무엇인가?

지수분포: very first event 에 대한 대기 시간을 예측

감마분포: k-th event 에 대한 대기 시간 예측

2. 감마분포의 PDF를 구해보자.

이전 포스트에서, 포아송 Process로부터 지수분포의 PDF를 유도해내었다. 만약 보지 못했다면 포아송 & 지수 분포에 대한 내용을 습득하고 오는 것이 좋을 것이다. 감마를 위해 꼭 완벽한 이해를 필요로 한다.

감마 분포의 PDF를 구하는 것은 지수 분포의 PDF를 구하는 것과 한 가지를 제외하고 매우 유사하다 –첫 번째 사건의 대기시간이 아닌, k-th event 발생 전까지의 대기시간!!!

<Notation!>
* T: k-th event까지의 대기시간을 나타내는 확률변수
    (이것이 관심 확률변수입니다)
* 사건 도달은 rate λ와 포아송 절차에 의해 모델링된다.

* k: 감마분포의 첫번째 파라미터. 기대하는 사건 갯수
* λ: 감마분포의 두번째 파라미터. 포아송 절차를 따르는 사건들의 rate

* P(T > t): k-th 사건이 발생하는 대기 시간이 t보다 더 클 확률
* P(X = k in t time units): t 단위 시간 내, k개의 사건이 발생하는 포아송 확률

이전과 같이, PDF를 구하기 위하여 CDF를 구하고 미분하도록 하자.

이제 미분을 진행하고자 하는데, x=0 일때 $e^{-\lambda t}$를 합산에서 제거하여 미분을 쉽게하고자 한다.

이제 감마분포의 PDF를 구했다. 미분식이 조금 복잡해보이긴 하지만, 변수 재조정, 미분의 곱셈법칙, 합 확산하고 좀 제거하는 등 꽤 간단한 과정들을 거쳤다.

미분식의 마지막 결과물을 보면, k=1일때의 지수분포의 PDF와 동일하다는 것을 파악할 수 있다.

k(사건 발생 횟수)는 양수이므로, $\Gamma(k) = (k-1)!$로 표현된다. 최종 결과는 다음과 같이 나타난다.

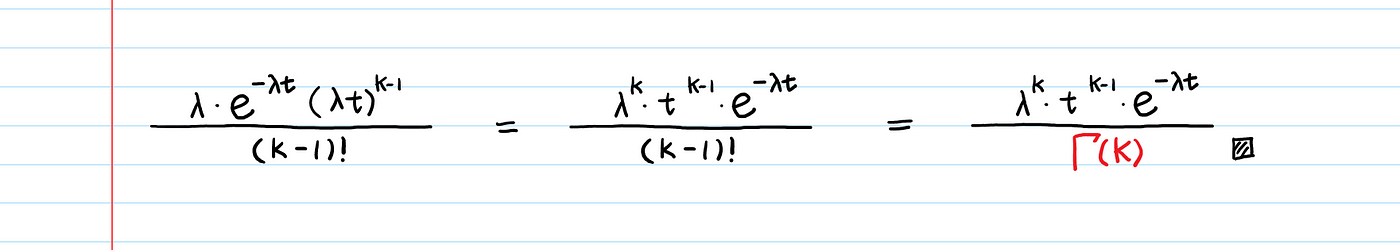
사건이 도달이 rate $\lambda$를 갖는 포아송 절차를 따른다면, k번의 도달에 대한 대기 시간은 $\Gamma(k, \lambda)$를 따른다.

감마분포의 파라미터: 모양 또는 scale?

감마분포의 파라미터에 대하여 혼동되는 두가지 관점이 있다.

관점 하나는 (k, θ) &(α, β)의 두 가지 다른 파라미터 세트와 PDF가 다른 형태라는 것이다. 관점 둘은 “scale” 파라미터에 대한 그 어떤 합의점도 없다!!

첫번째 문제는 쉽게 해결해버릴 수 있다.

(α, β) 파라미터화: k(사건의 갯수) & $\lambda$(사건의 rate)를 k는 $\alpha$로, $\lambda$는 $\beta$로 치환해버린다. PDF는 우리가 아는 모양 그대로 존속한다. (k, θ) 파라미터화: θ는 $\lambda$의 역수이며, 이는 평균 대기 시간이다.

PDF의 모양이 다른 꼴이지만, 두 파라미터화는 같은 모델을 생성한다. 일직선을 정의할 때와 같이, 어떨 때는 기울기와 y절편을, 다른 경우에는 x절편과 y절편을 활용하며, 이는 각자의 취향이다. 개인적 생각으로는 $\lambda$를 rate parameter로 활용하는 것이 가장 좋다고 생각하는 것이 포아송 rate $\lambda$에서 지수와 감마 분포를 이끌어 내는 것을 보았기 때문이다. 그리고 $\alpha$, $\beta$가 integrate에 용이하다.