포아송분포 - 직관, 유도, 예시 (Medium Post 번역)

Posted on | In |

본 포스트는 Medium의 Exponential Distribution에 대한 포스트를 번역한 것입니다. https://towardsdatascience.com/what-is-exponential-distribution-7bdd08590e2a

공식으로 바로 진입하기 전에 “왜”에 대하여 항상 생각해야 한다. 이유에 대하여 생각한다면, 더 이해가 잘 붙을 것이고, 너의 것으로 만들어 자신의 업무에 적용할 수 있을 것이다.

1. 왜 지수분포를 만들었는가?

다음 사건(성공, 실패, 도착 등) 전의 대기 시간을 예측하기 위하여!

예를 들어, 다음을 예측하고자 한다:

  • 가게에서 손님들이 구경을 다 마치고 실제로 상품을 구매하는데까지 걸리는 시간(success)

  • AWS EC2가 꺼져버리기 전까지의 시간(failure)

  • 버스가 도착하기 전까지의 대기시간(arrival)

그럼 다음 질문은… $\lambda*e^{-\lambda t }$ 가 대체 왜!! 다음 사건이 발생하기 전까지의 시간을 나타내는 PDF 인것인가?

그리고 이어지는 질문은… X~Exp(0.25)의 의미는 무엇인가? 0.25라는 수치는 0.25분인가? 시간인가? 날인가? 아니면 0.25 events인가??

지금부터는 당신이 Poisson을 알고 있다고 가정하고 진행할것이기 때문에, 만약 잘 모른다면 this article을 참고해주세요!

X~Exp($\lambda$) 의 $\lambda$는 포아송분포의 $\lambda$와 같은 파라미터인가?

X~Exp(0.25) 에 대한 혼란에 빠지지 않기 위해 알아두어야 하는 것은, 0.25가 time duration 이 아닌, event rate 라는 것이다. 즉, $\lambda$는 Poisson process의 것과 같은 것이다.

예를 들어, 블로그의 일일 방문자는 500명이다. 이것은 rate 이다.

  • 한시간에 가게에 방문하는 고객의 수
  • 연간 지진 발생 횟수
  • 주간 교통사고 발생 횟수
  • 한 페이지에 있는 글자 수
  • 패스트푸드 음식점에서 발견되는 머리카락 갯수 등 은 단위 시간의 rate($\lambda$)이며 이는 포아송분포의 파라미터이다.

하지만, 사건 사이의 시간을 모델링한다고 했을 때는 당연히 rate보다는 시간의 관점으로 논할 것이다.

  • 하나의 컴퓨터가 10년 이내에서 실패 없이 작동할 수 있는 기간 (0.1failure / year와 같은 rate로 말하지 않는다)
  • 고객이 매 십분마다 도달하는 것
  • 주요 허리케인은 매 7년에 한번씩 오는 것 용어를 살펴보자면……(번역이 조금 힘든 부분) When you see the terminology — “mean” of the exponential distribution — 1/λ is what it means.

지수분포에서 겪는 혼동은 “decay parameter” 또는 “decay rate”로부터 온다. decay parameter 란 시간(매 10분, 매 7년마다 등)으로 표현되며, 포아송 rate의 역수이다. ($1/\lambda$). 생각해보면: 한 시간에 3명의 고객이 있다면, 1/3시간마다 1명의 고객이 있다는 것이다.

그렇다면 이제 다음의 질문에 답할 수 있을 것이다. “X ~ Exp(0.25)는 무슨 의미인가?”

이는 포아송 rate가 0.25임을 의미한다. 단위시간(분이든, 시이든, 년이든)동안 평균적으로 eventrk 0.25번 나타난다는 것이다. 이것을 시간의 관점으로 전환하고, 단위 시간이 시간이라고 가정한다면, 사건 발생까지 4 hours(0.25의 역수)가 소요된다고 할 수 있다.

1
* Confusion-proof : Exponential‘s parameter λ is the same as that of Poisson process (λ).

2. 지수분포의 PDF를 구해보자!

우리의 첫 질문은: “$\lambda*e^{-\lambda t }$ 가 왜 다음 사건이 발생하는 시간으로 정의하는가” 였다.

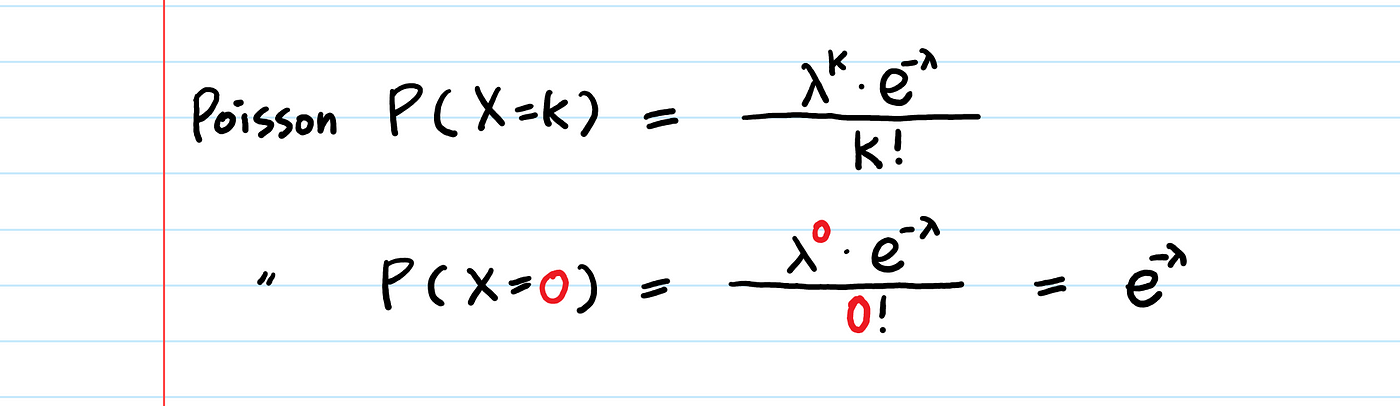
지수분포의 정의는 포아송 process의 사건들 사이 시간의 확률 분포이다. 생각해본다면… 사건이 발생하기 전까지의 시간이란, 해당 시간동안 하나의 event도 발생하지 않는다는 것이다. 즉, Poisson(X=0)을 의미한다. poisson X = 0

*Poisson(X=0): 지수분포를 구하기 위한 미분과정의 첫 step*

포아송 PDF에 대하여 기억하고 있어야 할 것은, 하나의 Poisson events(X=k)가 발생하기 위한 시간은 (1) Unit Time이다.

만일 “하나의 단위 시간이 아닌, time duration t에서 아무일도 발생하지 않음”을 확률 분포로 나타내고 싶다면 어떻게 해야하는가?

1
2
3
4
P(t time units에서 아무일도 벌어지지 않음) =
P(X=0 in the first time unit) * P(X=0 in the second time unit) * ... *
P(X=0 in the t-th time unit)
= e^−λ * e^−λ * … * e^−λ = e^(-λt)

포아송 분포는 각 사건들이 독립적이라고 가정한다. 따라서 t units of time의 0개의 success에 대한 확률을 P(X=0 in a single unit of time)을 t번 곱해서 구할 수 있다.

1
2
3
4
5
6
P(T > t) = P(X=0 in t time units) = e^−λt
* T : 우리의 관심 대상인 확률변수!
      첫 번째 사건이 발생하는 대기 시간에 대한 확률변수
* X : 포아송분포를 따르는 사건 횟수
* P(T > t) : 첫 사건의 대기시간이 t 단위시간보다 클 확률
* P(X = 0 in t time units) : t 단위 시간에서 사건이 발생하지 않을 확률!

PDF는 CDF의 미분이다. 우리는 이미 CDF, 1-P(T>t)가 있으므로, 이를 미분하여 PDF를 구해버릴 수 있다.

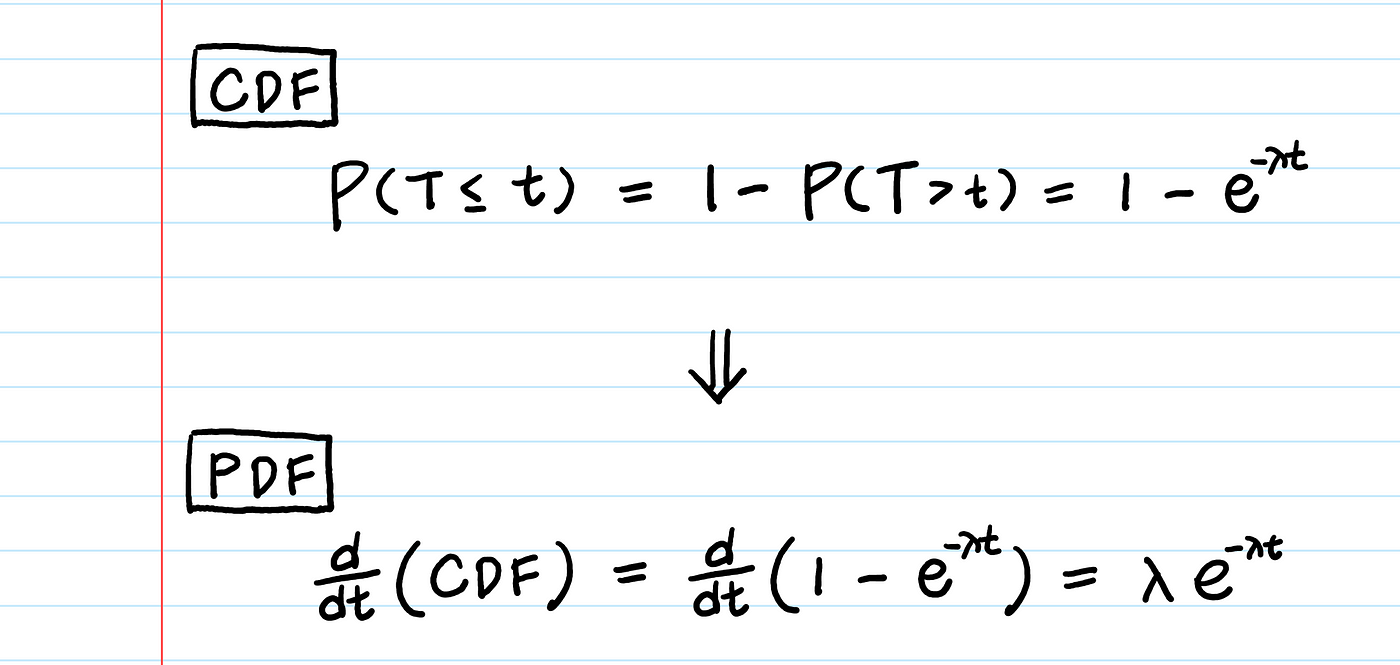
poisson X = 0

3. 무기억성 (Memoryless Property)

1
2
Definition:
P(T > a+b | T > a) = P(T > b)

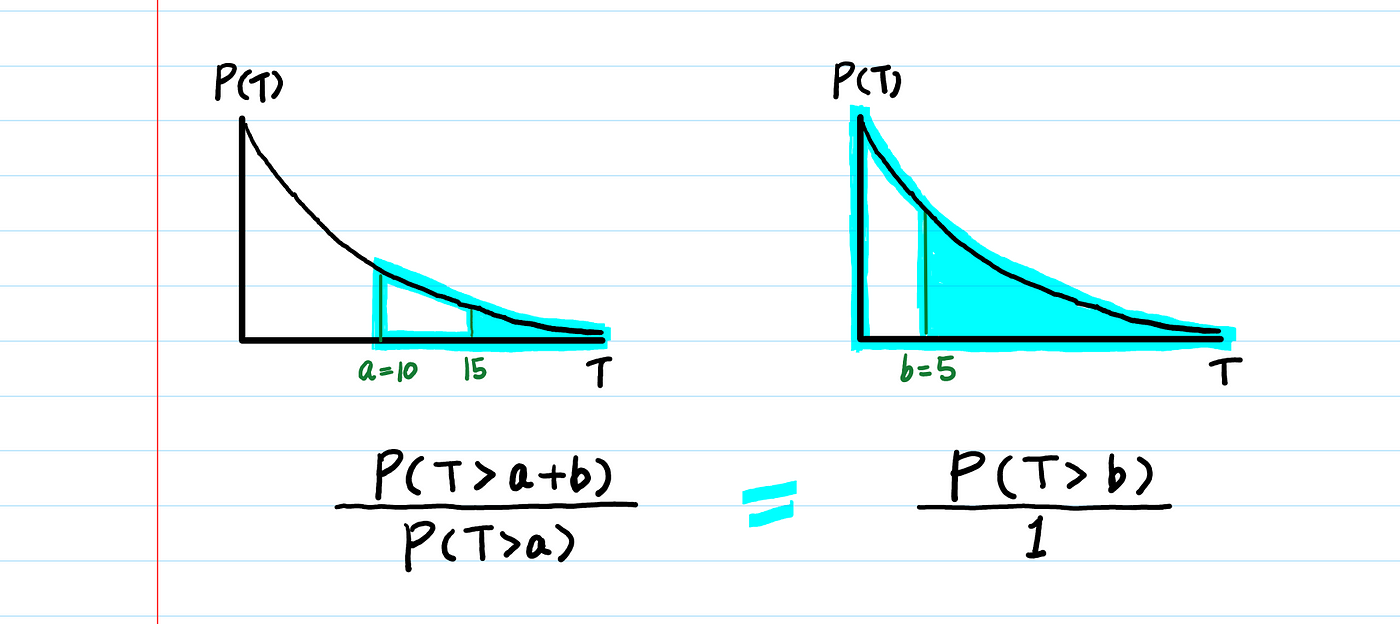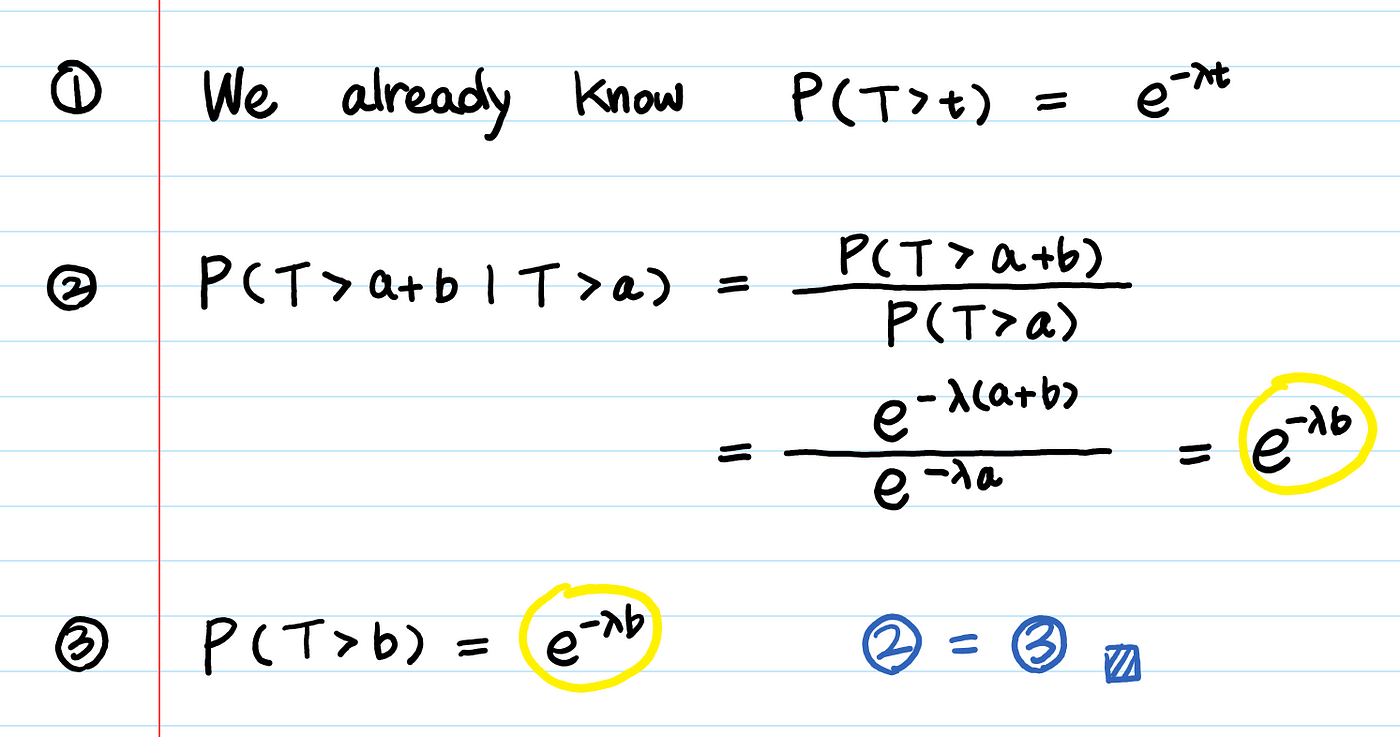
poisson X = 0 증거? 증거 있지. poisson X = 0

이 무기억성이라는 것이 효용성이 있는가?

기계의 수명을 지수분포를 활용해서 모델링하는 것이 현명한 것인가?

예를 들어, 기계가 이미 9년동안 버티고 있는 중이고, 무기억성에 의하면 추가 3년을 더 버틸 수 있는 것과(총 12년) 완전 새로운 기계가 3년동안 버틸 것이라는 것과 같은 의미이다.

1
P(T > 12 | T > 9) = P(T > 3)

이게 맞는 말처럼 보이십니까? 나에겐 그렇지 않아… 내 경험에 의하면 오래된 기계가 더 고장날 가능성이 높지. 이 속성-hazard rate 증가-를 모델링하기 위해선 Weibull distribution을 사용해야 한다.

그럼 (일정한 hazard rate)를 갖는 지수분포를 사용하기에 적당한 상황은 뭐야?

자동차 사고가 있다. 5시간 전에 누가 들이받지 않았다고 해서 너가 자동차 사고를 당할 확률이 증가 또는 감소하지 않을 거자나?

무기억성을 갖는 다른 놈들은 없나?

지수 분포가 (연속분포에서) 유일무이한 무기억성을 갖는 분포이다. (이산분포에서는) 기하분포가 있다.