본 포스트는 Medium의 poisson distribution에 대한 포스트를 번역한 것입니다. https://towardsdatascience.com/poisson-distribution-intuition-and-derivation-1059aeab90d

포아송 분포의 파라미터인 $\lambda$를 공식에 넣기 전에, 잠시 고민해보자!

애초에 왜 포아송분포를 만들었는가?
(왜 이 분포가 존재하는가?)
모델링에서 포아송분포가 언제 사용되어야 하는가?

1. 왜 포아송분포를 만들었는가?

Answer: 미래에 발생가능한 사건들의 횟수를 예측! 좀 더 Formal하게는… 정해진 시간 내에 주어진 횟수의 사건이 발생할 확률을 예측!

예를 들어, 고객이 당신에게 물건을 사고, 물건을 판매하는 상황을 가정해보자. 또는, 당신의 웹사이트에 방문자가 몇 명이고, 다음달에 광고 클릭이 얼마나 될 것인지, 당신의 업무 시간에 전화가 얼마나 올 것인지, 또는 내년의 질병으로 인한 사망자가 얼마나 될 지에 대한 문제일 수 있다.

아래는 내가 실생활에서 포아송 분포를 사용할 수 있는 예시이다.

매주, 평균적으로, 나의 블로그 게시물에 17명이 좋아요를 눌러준다.
나는 이 좋아요를 통해 돈을 벌기 때문에, 다음 주 좋아요 갯수를 예측하고 싶다.

* 다음 주 게시글에서 20명(또는 10,30,50)이 좋아요를 눌러 줄 확률은?

2. 포아송분포를 모른다고 가정하면, 이 문제를 어떻게 풀 것인가요?

하나의 방법은, 읽은 횟수로부터 시작하면 된다. 일단 ‘좋아요’를 누르기 위해선 포스트를 읽는 것이 먼저이며, 읽은 후에 정말 마음에 들어 좋아요를 누를 수 있기 때문이다.

이는 이항 분포에서는 흔한 일인데, 성공 횟수의 확률을 계산하기 때문이다.

이항 확률 변수(binomial random variable)는 n번의 반복 측정에서 성공 횟수 x이다. 그리고 p를 각 시행에서 성공의 확률이라고 가정한다.

하지만 이 문제에서 우리는 “RATE”로 표현되는 단 하나의 정보만을 갖고 있다. – 17 ppl / week (주당 성공 횟수의 평균 / 또는 x의 Expectated Value(기댓값)) 우리는 “좋아요”의 확률 p나 방문자수 n에 대한 정보가 없다.

따라서 우리는 이 문제를 해결하기 위해 더 많은 정보들이 필요하다. 이항 문제로 해결하면 쉬울 것 같은데 어떤 정보들이 추가되어야 이항 관련 문제로 전환하여 풀어낼 수 있을까?
우리는 두가지 정보가 필요하다:

성공 확률 p
시행 횟수 n

과거의 데이터를 통해 두 변수를 채워나가보자.

1년 간의 통계에서 59k의 사람들이 블로그에 방문을 했고, 그 중 888명이 “좋아요”를 눌러주었다. 따라서, 주당 방문객 수(n)는 59k/52 = (1134)이며, 주당 “좋아요” 갯수는 888/52 = (17)이다.

# of people who read per week (n) = 59k / 52 = 1134
# of people who clap per week (x) = 888 / 52 = 17
Success probability (p): 888 / 59k = 0.015 = 1.5%

이항분포의 PMF를 통해 다음주에 20개의 “좋아요”를 얻는 확률은 어떻게 될까?

$\binom{n}{k}\cdot p^k(1-p)^{n-k}$ = $\binom{1134}{20} \cdot 0.015^{20}(1-0.015)^{1134-20}$ = 0.06962

사실 이렇게 풀어재끼면 문제 없는 것인데 포아송은 왜 있는 것일까? 포아송은 가능하지만, 이항분포는 불가한 것이 있을까?

#3. 이항분포의 결점

a) A binomial random variable is “BI-nary” – 0 or 1

위의 예시에서, 17ppl/week의 “좋아요”를 얻었다. 그 뜻은 하루로는 17/7 = 2.4명의 “좋아요”를 의미하며, 한 시간으로는 17/(7*24)의 “좋아요”를 의미한다.

만약 시간당 “좋아요”를 통해 이항 확률 변수를 구성한다면, 대부분의 시간에서는 0의 “좋아요”, 그리고 몇몇의 시간에서 1개의 “좋아요”를 얻을 것이지만, 아주 가끔 1보다 큰 “좋아요”를 얻을 수도 있다.

이항의 문제는 하나의 시간 단위는 하나의 event만을 포함할 수 밖에 없다는 것이다.(한 시간이 단위시간). 하나의 단위 시간은 0 또는 1개의 event를 갖는다.

그렇다면 이 단위시간을 다시 한 시간에서 60분으로 나누어 단위시간을 지속적으로 줄여나가면 어떻게 될까? 그럼 한 시간은 다중의 event를 갖게 될 것이다. (그리고 1분은 0 또는 1의 사건을 갖게 될 것이다.)

이걸로 우리의 문제가 해결되었는가? (역주: 띄용?)

이런식으로 지속적으로 단위시간이 작으면 작아질 수록 같은 문제가 계속 발생할 것이다.

IDEA: 이항 확률 변수의 단위를 지속적으로 줄여나가면 하나의 기존 단위가 1개 이상의 events들을 담게 할 수 있다. 즉, 더 잘게 쪼겐 단위를 이용하게 된다면, 기존의 단위 시간이 하나 이상의 event를 포함하게 된다.

수학적으로 이는 n -> $\infty$이며, RATE(17 ppl / week)는 고정되어 있으므로 p -> 0으로 설정해야 한다. 그렇지 않으면, n*p, 사건의 갯수가 폭발하게 될 것이다.

극한을 사용한다면, 단위 시간은 이제 극소가 될 것이다. 이제 더 이상 단위 시간에서 하나 이상의 단위 시간이 나타날 것을 걱정하지 않아도 된다. 이것이 포아송분포를 유도하는 방법이다.

b) In the Binomial distribution, the # of trials (n) should be know beforehand.

이항분포를 사용한다면, 전체 성공확률을 계산하기 위해서는 (17ppl/week)과 같은 “RATE” 뿐만이 아니라 (n&p)와 같은 것들이 있어야 이항분포 PMF를 사용할 수 있다.

그에 반해, 포아송분포는 n 또는 p를 몰라도 된다. 우리는 n이 엄청나게 크고, p가 매우 작다고 가정하며, 포아송분포에서 필요한 유일한 파라미터는 rate $\lambda$(Expected value of x) 이다. 실제 상황에서는 n & p를 아는 것보다, RATE(i.e., 2~4pm에 3번의 전화가 왔다)를 아는 것이 더 현실적이다.

4. Binomial PMF에서 Poisson 공식을 유도해보자!

이로써, $\lambda^k, k!, e^{-\lambda}$의 출처를 알게 되었으며, 마지막으로 $n!/((n-k)!*n^k)$가 n이 무한대로 뻗어나갈 때 1이 됨을 보이면 끝난다!

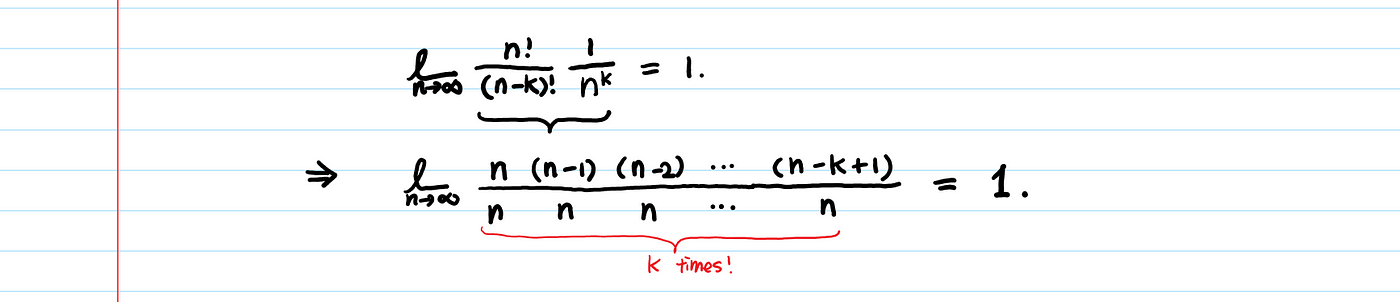
이제 위키백과의 설명이 얼추 아다리가 맞아 보인다.

몇가지 더 생각해볼만한 것:

포아송분포가 rare events를 모델링하지만, rate $\lambda$는 어떤 수도 가능하다. 반드시 작아야 할 필요는 없다.
포아송분포는 비대칭이며, 우측으로 skewed되어 있다. “-1개의 좋아요”와 같은 일이 없는 ‘zero occurence barrier’가 있기 때문에 오른쪽으로만 무제한으로 펼쳐진다.
$\lambda$가 커지면, 정규분포화한다.

포아송분포 가정들

a. 단위시간에 대한 사건의 평균 RATE 상수이다.

b. 사건들이 독립이다.(또는 아닐 수도 있긴 하다) 블로그 방문객의 도달 그 자체는 독립이 아닐 수 있다. 예를 들어 다수의 방문객들이 유명인의 언급에 의해 접속할 수 있거나, Medium의 First Page에 등록이 되는 것과 같은 일이 있을 수 있기 때문이다. 한 나라의 연간 지진 횟수는 포아송분포를 따르지 않을 수 있는데 하나의 지진이 연쇄적으로 후의 지진에 영향을 미칠 수 있기 때문이다.

5. 포아송분포와 지수분포의 관

만약, 단위 시간 당 사건 발생 빈도가 포아송분포를 따른다면, 사건 간의 시간은 지수분포를 따른다. 포아송분포는 이산적이고 지수분포는 연속적이지만, 매우 깊게 연관되어 있다.

Let’s go deeper: Exponential Distribution Intuition