본 포스트는 Medium의 Conjugate Prior에 대한 포스트를 번역한 것입니다. https://towardsdatascience.com/conjugate-prior-explained-75957dc80bfb

Prior란 무엇인가?

사전 확률은 데이터를 관찰하기 이전의 사건의 확률을 의미한다. 베이지안 추론에서 사전은, 새로운 데이터가 사용 가능하기 전에, 현재 알고 있는 정보로 나타낸 확률이다.

WTF is Conjugate Prior?

이 켤레 사전이란 베이지안 inference를 모르고는 아모고토 이해하지 못할 것이다. 이후의 포스트에서는 prior, sampling 그리고 posterior에 대해서 알고 있다고 가정하겠다.

Conjugate prior in essence

몇몇의 Likelihood functions에 대하여, 특정한 prior를 선택했다면, posterior는 결국 prior와 같은 분포를 갖는 결론에 다다른다. 이런 prior를 Conjugate Prior라고 부른다.

항상 예시를 통한 이해가 가장 좋다. 아래는 이항 가능도에 대한 posterior를 계산하기 위한 코드이다. $\theta$는 성공 확률이며 posterior를 최대로 하는 $\theta$를 찾는 것이 목적이다.

import numpy as np
import scipy.stats as stats

success_prob = 0.3
data = np.random.binomial(n=1, p=success_prob, size=1000) # sucess is 1, failure is 0.

# Domain θ
theta_range = np.linspace(0, 1, 1000)

# Prior P(θ)
a = 2
b = 8
theta_range_e = theta_range + 0.0001
prior = stats.beta.cdf(x = theta_range_e, a=a, b=b) - stats.beta.cdf(x = theta_range, a=a, b=b)

# The sampling dist. aka Likelihood P(X|θ)
likelihood = stats.binom.pmf(k = np.sum(data), n = len(data), p = theta_range)

# Posterior
posterior = likelihood * prior
normalized_posterior = posterior / np.sum(posterior)

질문: 코드에서 아리까리하 내용이 있는가? 여기에는 posterior 계산을 복잡하게 하는 두 가지 요소가 있다.

###First, 모든 $\theta$에 대한 posterior를 계산하고 있다.

왜 무수히 많은 theta에 대하여 posterior를 계산하고 있을까? 그 이유는 (line 21) posterior를 정규화하고 있기 때문이다. Posterior를 정규화하지 않도록 결정했다 하더라도, posterior의 최대를 찾는 것이 궁극적인 목표이다 (Maximum a posteriori). 최대를 기본적인 방법으로 찾는다고 한다면, 우리는 모든 후보를 고려해야 한다. -the likelihood P(X

θ) for every θ-

Second, posterior에 대한 closed-form formula가 존재하지 않는다고 한다면, 우리는 수치적으로 최적화(gradient descent, newton’s method)를 진행해서 maximum을 구해야 한다.

3. Conjugate가 어떻게 도움이 되려나?

만약 prior가 conjugate prior라면 posterior=likelihood * prior를 건너 뛰어도 된다. 게다가, 만일 prior distribution이 closed-form 형식이라면, maximum posterior가 어디로 도달할 지 알 수 있을 것이다.

위의 사례에서 베타 분포가 binomial likelihood의 conjugate prior라는 것을 알 수 있다. 이것이 무엇을 의미하는가? 이는 모델링 과정에서 posterior 또한 beta 분포가 될 것이라는 뜻이다. 따라서, 몇 번의 실험을 더 한 뒤에, posterior의 기존의 $\alpha, \beta$에 성공과 실패의 숫자를 계속 더해나가며 posterior를 구성해나갈 수 있다!(다음 섹션에서 증명)

Data/ML 사이언티스트로서 모델을 완벽할 수 없다. 데이터가 더 추가되면서 지속적으로 업데이트를 해나가야 한다. 보았듯이, 베이지안 추론의 계산은 부담되거나 어려울 수 있다. 하지만 conjugate prior의 closed-form을 활용한다면 계산이 매우 쉬워질 것이다.

4. Proof — Why is a Beta distribution a conjugate prior to Binomial likelihood?

prior를 베타분포로 활용한다면, binomial likelihood의 posterior는 beta를 따르게 될 것이다.

Beta가 Beta를 부른다.

Binomial과 Beta의 PDF의 생김새가 어떤지 봐보자.

이를 베이즈 공식에 넣어보자.

$\theta$ = 성공의 확률 x = 성공의 횟수 n = 시도 횟수, n-x는 실패 횟수

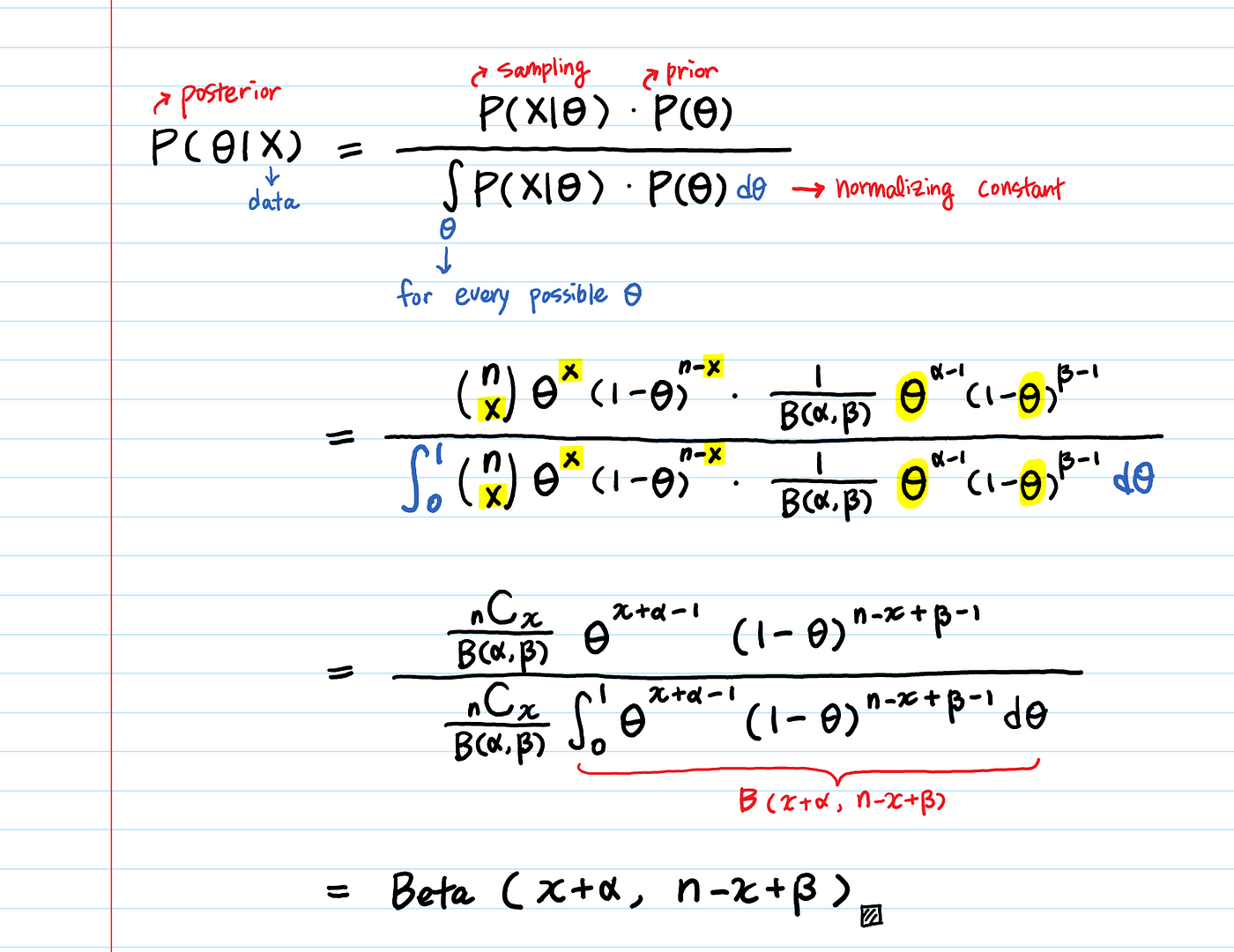
사전분포 $P(\theta)$는 $Beta(\alpha, \beta)$이며, x의 성공과, n-x의 실패를 한 뒤, posterior는 $(x+\alpha, n-x+\beta)$의 파라미터를 갖는 Beta 분포가 된다.

계산을 딱히 안해도 구조적으로 이게 왜 이렇게 되는 지 알 수 있을 것이다(역주: 뭔 개소리를 하시는 지 모르겠습니다!!)

#5. Conjugate Prior Distributions Beta 분포는 Bernoulli, binomial, negative binomial and geometric distributions의 켤레사전분포이다(성공과 실패를 포함하는 분포)

<Beta posterior>
Beta prior * Bernoulli likelihood → Beta posterior
Beta prior * Binomial likelihood → Beta posterior
Beta prior * Negative Binomial likelihood → Beta posterior
Beta prior * Geometric likelihood → Beta posterior
<Gamma posterior>
Gamma prior * Poisson likelihood → Gamma posterior
Gamma prior * Exponential likelihood → Gamma posterior
<Normal posterior>
Normal prior * Normal likelihood (mean) → Normal posterior

이것이 분포계의 (노답) 삼형제, Beta, Gamma, Normal이 많이 쓰인 이유이다.

prior와 likelihood를 아무리 많이 곱하는 실험을 했어도, 결국 prior distribution의 최초의 선택이 너무 좋아서 최후의 분포가 prior와 같을 것이다. 즉, $P(\theta)$를 식으로 표현하자면

1	`P(θ) such that P(θ\|D) = P(θ)`

Conjugate Prior=Convenient Prior

A few things to note:

Conjugate Prior를 활용할 때, sequential estimation(매 관찰마다 업데이트)은 batch estimation과 같은 결과를 줄것이다.
Maximum posterior를 찾기 위해, likelihood와 prior의 곱샘에 대한 정규화를 안해도 된다.

정규화없이도 maximum을 찾을 수 있지만, posterior를 다른 모델과 비교하고 싶다면, 또는 점 추정을 계산하고 싶다면 정규화가 필요하다.