본 포스트는 Medium의 Bayesian Inference에 대한 포스트를 번역한 것입니다. https://towardsdatascience.com/bayesian-inference-intuition-and-example-148fd8fb95d6

어떤 자식이 애초에 ‘베이지안 추론’ 이라는 것을 만들었느냐…왜!!!!

한마디로: 더 많은 데이터를 모으면서 지속적으로 확률을 업데이트 하고 싶을 때…

베이지안 추론의 핵심은 두 개의 다른 분포(likelihood와 prior)를 더해 하나의 “Smarter” 분포(posterior)를 만드는 것이다. 사후 분포는 전통적인 최대 가능도 예측이 사전 분포를 포함하지 않는 부분에서 더 똑똑하다. 사후 분포를 계산했다면, “최고의” 파라미터를 찾을 때 활용하며, “최고”란 사후 확률을 최대화 하는 관점에서 말하는 것이다. 이 절차를 Maximum A Posteriori(MAP)라고 부른다. 이 MAP에서 활용되는 최적화 방법은 경사하강법이나, 뉴턴’s method와 같은, 전형적인 머신러닝에서 활용되는 것과 같다.

유명한 Bayes rule을 살펴볼 때, 식을 분석적으로 이해하는 것은 어렵지 않다. 하지만 이를 데이터에 어떻게 적용할래?

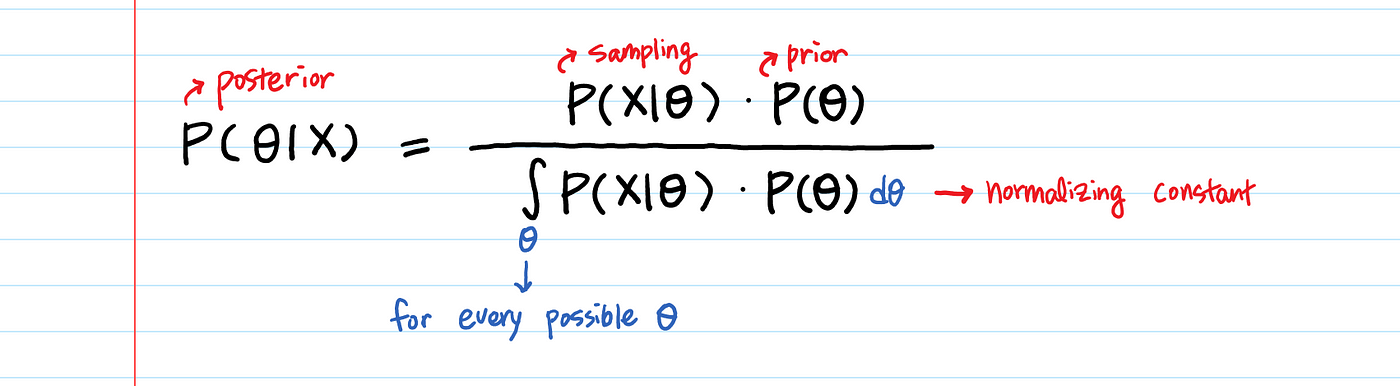
우리는 많은 량의 데이터 포인트 X를 가질 것이다. X에 관련된 확률과 $\theta$에 관련된 확률을 어떻게 곱할 것인가? 그런 조합은 매우 많을 것이다.

즉, 베이지안 추론은 어떻게 다루느냐에 따라서 빛이 날 수 있다.

Example:

나의 Medium 블로그에는 2천명의 독자가 방문한다. 몇명은 “좋아요”를 누르지만 몇은 그렇지 않는다. 나는 이후에 새로운 게시물을 올렸을 때, 몇 퍼센트의 사람들이 “좋아요”를 누르는지에 대한 예측을 해보고 싶다. 내가 모은 “좋아요”데이터는 이진 데이터이며, 1은 “좋아요”, 0은 없음을 의미한다.

이런 문제는 넓게 적용 가능하다. 너만의 문제에 적용해보려고 노력해봐라…

Generating Data:

먼저 X 데이터를 구축해보자! (실제로는 X에 대한 주도권이 없이, 주어진대로 진행해야 한다.)

import numpy as np
np.set_printoptions(threshold=100)
# Generating 2,000 readers' reponse.
# Assuming the claps follow a Bernoulli process - a sequence of binary (success/failure) random variables.
# 1 means clap. 0 means no clap.
# We pick the success rate of 30%.
clap_prob = 0.3
# IID (independent and identically distributed) assumption
clap_data = np.random.binomial(n=1, p=clap_prob, size=2000)

데이터 X는 다음과 같이 나타난다:

In [1]: clap_data
Out[1]: array([0, 0, 0, ..., 0, 1, 0])
In [2]: len(clap_data)
Out[2]: 2000

베이지안 추론은 세 단계로 이루어진다.

Step 1. [Prior] Parameter $\theta$를 모델링 할 PDF를 선택한다, AKA prior_distribution $P(\theta)$. 이는 data X를 보기 이전의 최선의 추측이다.

Step 2. [Likelihood] $P(X

\theta)$를 위한 PDF를 선정. 기본적으로 파라미터 $\theta$가 주어졌을 때 data X가 어떻게 생길 지에 대한 모델링이다.

Step 3. [Posterior] 사후 분포 $P(\theta

X)$를 계산하고 $P(\theta

X)$를 최대화하는 $\theta$를 찾아라!

그러면 Posterior가 새로운 Prior로 전환된다. 이것을 데이터를 더 얻게 된다면 3번정도 반복하면 된다.

Step 1: Prior $P(\theta)$

첫번째로 파라미터 $\theta$를 모델링 하는 PDF를 선택한다.

파라미터 $\theta$는 무엇을 나타내는가?

“좋아요”의 확률이다.

그렇다면, 확률을 모델링하기 위해선 어떤 확률 분포를 사용해야 하는가?

확률을 표현하기 위해선 몇가지 조건을 만족해야 한다.

정의역은 0~1사이어야 한다.
연속분포여야 한다.

그렇다면 우리가 생각할 수 있는 두 개의 유명한 분포는:

Beta and Dirichlet

디리클레는 다변량을 위한 것이고 베타는 단변량을 위한 분포이다. 우리는 확률이라는 단 한가지만을 예측해야 하므로, Beta 분포를 사용하도록 하자.

베타 분포를 활용하기 위해선 두 가지 파라미터($\alpha$ & $\beta$)가 필요하다. $\alpha$: “좋아요”를 누르는 사람 수 $\beta$: “좋아요”를 누르지 않는 사람 수

이 파라미터들이 분포의 모양을 결정할 것이다.

만약 어제의 데이터를 통해 2000명 중 400명이 “좋아요”를 눌렀다고 해보자. 그럼 이것을 beta distribution으로 어떻게 표현할 것인가?

import scipy.stats as stats
import matplotlib.pyplot as plt
a = 400
b = 2000 - a
# domain θ
theta_range = np.linspace(0, 1, 1000)
# prior P(θ)
prior = stats.beta.pdf(x = theta_range, a=a, b=b)

이제 모든 $\theta$에 대하여 사전 분포를 작성해보자.

# Plotting the prior distribution
plt.rcParams['figure.figsize'] = [20, 7]
fig, ax = plt.subplots()
plt.plot(theta_range, prior, linewidth=3, color='palegreen')
# Add a title
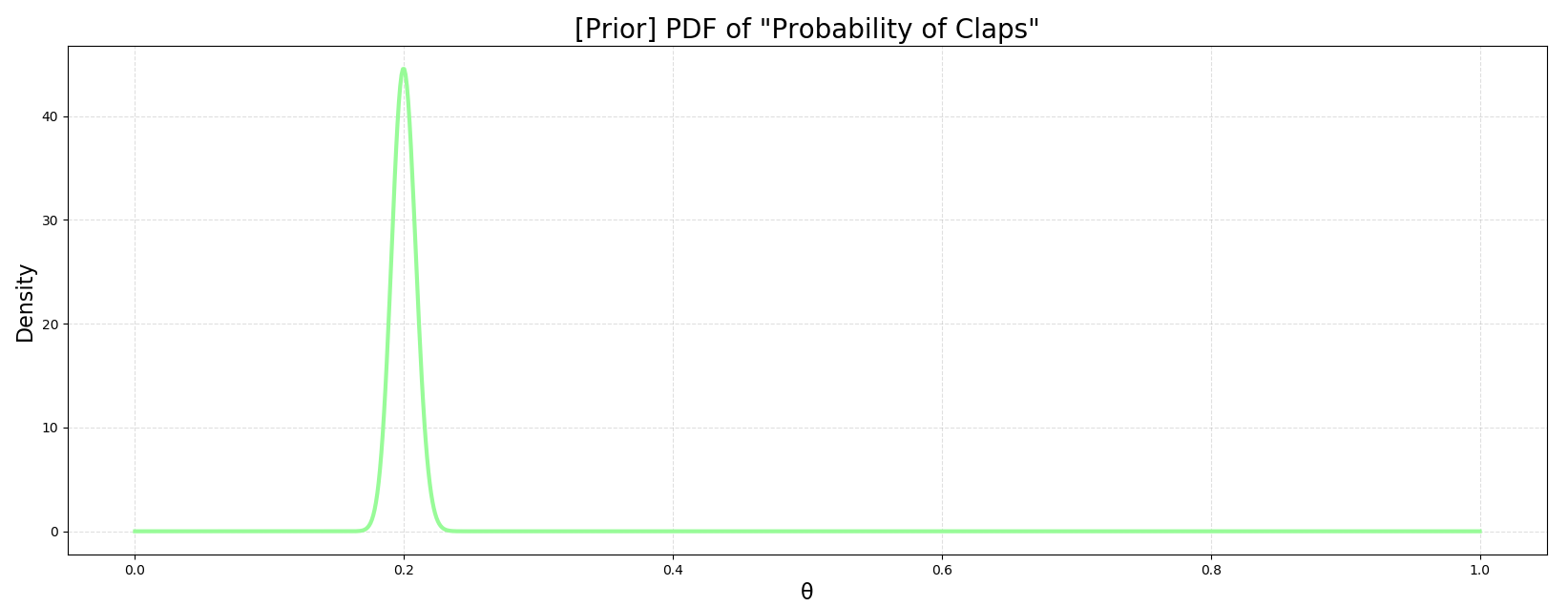
plt.title('[Prior] PDF of "Probability of Claps"', fontsize=20)
# Add X and y Label
plt.xlabel('θ', fontsize=16)
plt.ylabel('Density', fontsize=16)
# Add a grid
plt.grid(alpha=.4, linestyle='--')
# Show the plot
plt.show()

예상대로 20%에서 급상승하는 모습이다 (400 “좋아요” / 2000 readers). 2천 개의 데이터가 꽤 강한 사전분포를 만들어준 것으로 보인다. 만약 100명과 같은 더 적은 데이터를 활용한다면 curve는 더 낮게 솟을 것이다. α = 20 & β = 80으로 한번 진행해보길 바란다.

Step 2: Likelihood $P(X|\theta)$

$P(X	\theta)$를 위한 확률 모델을 선택해보자. 이는 파라미터 $\theta$가 주어졌을 때 data X를 관찰할 확률을 말한다. Likelihood란 sampling distribution이라고도 불린다. 나에겐 “sampling distribution”이 “likelihood”보다 더 직관적으로 느껴진다.

Sampling 분포를 모델링할 때 사용할 확률 분포를 선택하기 위해선 먼저,

우리의 데이터, X가 어떻게 생겼는지 알아야 한다

X는 [0,1,0,1,…,0,0,0,1] 꼴의 이진 배열이다.

우리는 (n)의 전체 방문객 수와 “좋아요” 수, 그리고 X로부터 “좋아요”의 확률(p)을 갖고 있다.

n & p 꼴이라… 이 어디서 보지 않았는가?

이항분포의 n & p를 활용해 “좋아요”의 횟수를 예측해보자.

# The sampling dist P(X|θ) with a given clap_prob(θ)
likelihood = stats.binom.pmf(k = np.sum(clap_data), n = len(clap_data), p = clap_prob)

가능한 X들과 특정 $\theta$=0.3을 통해 $P(X

\theta)$의 그래프를 그려내보자.

# Domain (# of claps)
X = np.arange(0, len(clap_data)+1)
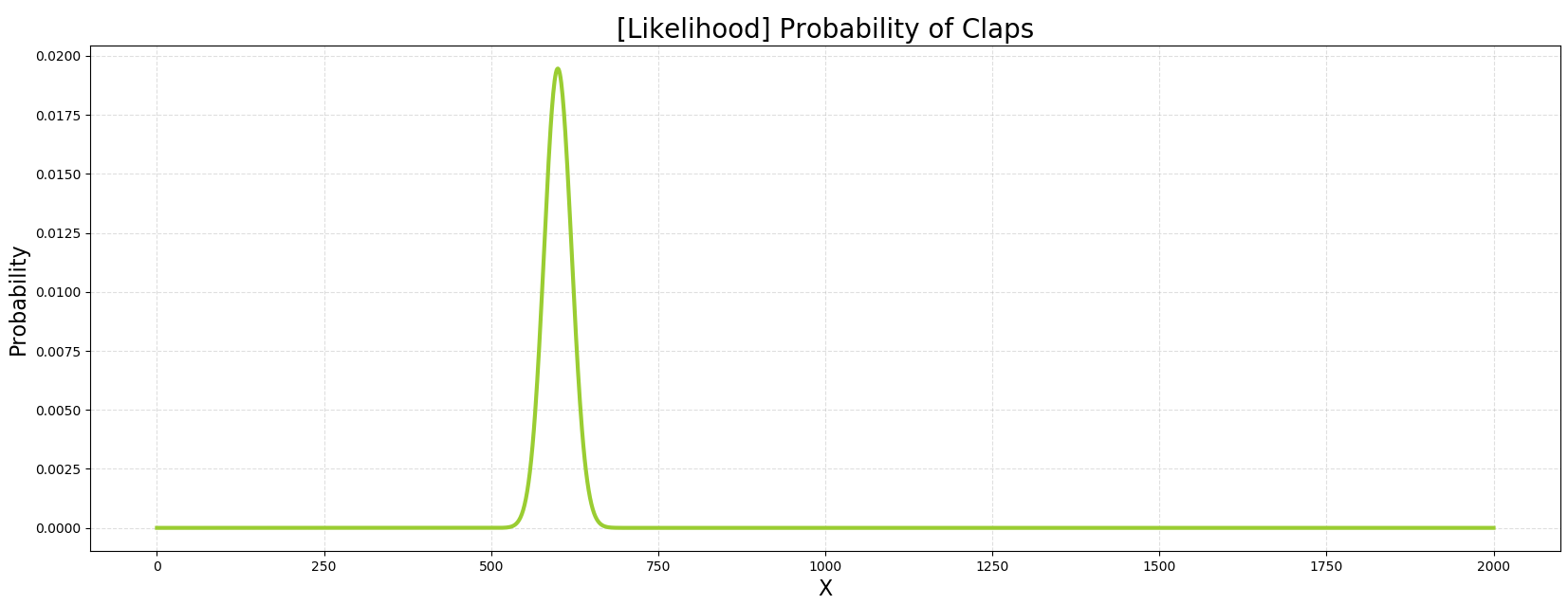
# Likelihood P(X|θ) for all X's
likelihood = stats.binom.pmf(k = X, n = len(clap_data), p = clap_prob)
# Create the plot
fig, ax = plt.subplots()
plt.plot(X, likelihood, linewidth=3, color='yellowgreen')
# Add a title
plt.title('[Likelihood] Probability of Claps' , fontsize=20)
# Add X and y Label
plt.xlabel(’X’, fontsize=16)
plt.ylabel(’Probability’, fontsize=16)
# Add a grid
plt.grid(alpha=.4, linestyle='--')
# Show the plot
plt.show()

본 그림이 $\theta$를 30%로 설정했을 때, n번 시행에 X번의 성공의 확률이다.

Step 3: Posterior $P(\theta|X)$

마지막으로, 맨처음 질문에 대한 답을 해보자.

우리는 많은 양의 데이터 포인트 X를 가질 것이다. X에 관련된 확률과 $\theta$에 관련된 확률을 어떻게 곱할 것인가? 그런 조합은 매우 많을 것이다.

베이지안 추론의 진정한 목적은 데이터에 가장 적합한 $\theta$를 찾는 것이다.

우리의 파라미터에 대한 최초의 추측은 $P(\theta)$이다. 이제 이 단순한 $P(\theta)$를 데이터가 많아질수록 $P(\theta

X)$와 같이 더 유용한 것으로 전환시킬 수 있다.

$P(\theta

X)$는 여전히 $\theta$에 대한 확률일테지만, $P(\theta)$보다는 더 똑똑한 버전이다.

어떻게 X에 대한 multiple probabilities와 $\theta$에 대한 multiple probabilities를 곱할 수 있을까??

비록 수많은 데이터들이 존재하지만 그것들을 선택한 모델(예를 들어 이항분포)에 데이터를 넣음으로써 단일의 scalar로 –$P(X

\theta)$–바꿀 수 있다.

그 후, 특정한 $\theta$에 대하여 $P(\theta)$ & $P(X

\theta)$ 를 계산한 뒤 곱해버리자. 모든 가능한 $\theta$에 대하여 진행한 다음, $P(\theta)* P(X

\theta)$ 중 최강을 찾아내자.

기본적으로, $\theta$를 가정한 뒤에 $P(\theta)$와 $P(X

\theta)$의 곱셉을 할 수 있다.

백번의 말보다 한번의 코드가 더 와닿을 수 있다:

# (cont.)
theta_range_e = theta_range + 0.001
prior = stats.beta.cdf(x = theta_range_e, a=a, b=b) - stats.beta.cdf(x = theta_range, a=a, b=b)
# prior = stats.beta.pdf(x = theta_range, a=a, b=b)
likelihood = stats.binom.pmf(k = np.sum(clap_data), n = len(clap_data), p = theta_range)
posterior = likelihood * prior
normalized_posterior = posterior / np.sum(posterior)

fig, axes = plt.subplots(3, 1, sharex=True, figsize=(20,7))
plt.xlabel('θ', fontsize=24)
axes[0].plot(theta_range, prior, label="Prior", linewidth=3, color='palegreen')
axes[0].set_title("Prior", fontsize=16)
axes[1].plot(theta_range, likelihood, label="Likelihood", linewidth=3, color='yellowgreen')
axes[1].set_title("Sampling (Likelihood)", fontsize=16)
axes[2].plot(theta_range, posterior, label='Posterior', linewidth=3, color='olivedrab')
axes[2].set_title("Posterior", fontsize=16)
plt.show()