본 포스트는 고려대학교 산업경영공학과 김성범 교수님의 예측모델 수업에서 부여된 과제를 푸는 과정에서 얻게 된 지식들을 정리한 것입니다.
(1) SVM (분류), SVR (예측) 모델을 하이퍼파라미터를 다양하게 바꾸어서 구축하시오 (kernel function, C, …)
SVM (분류)
SVM의 대표적으로 활용되는 Parameter List는 다음과 같습니다.
-
C: float, default=1.0
C는 Regularization cost로서 Margin의 넓이와 Margin에서 벗어나는 값들의 Penalty에 대하여 Trade-off를 조절해주는 역할을 합니다.
- 큰 C: Penalty를 최대한 허용하지 않으므로, Margin의 크기도 줄어듭니다.
- 작은 C: Penalty를 최대한 허용하므로, Margin의 크기도 넓어집니다.
-
kernel : {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’}, default=’rbf’
-
degree: int, default=3
- Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.
Degree는 Polynomial Kernel을 사용할 때, 다항식의 차수를 나타내는 것입니다.
-
gamma: {‘scale’, ‘auto’} or float, default=’scale’*
-
if
gamma='scale'(default) is passed then it uses 1 / (n_features * X.var()) as value of gamma, -
if ‘auto’, uses 1 / n_features.
gamma는 $1/sigma^2$을 뜻하여,
- 값이 커지면 분산이 작아져, Gaussian Kernel이 첨예해집니다.
- 값이 작아지면 분산이 커져, Gaussian Kernel이 넓어집니다.
RBF 커널의 분산이 작아질수록 복잡한 decision boundary가 생성되는데, 이는 함수 복잡도가 커지는 것이다. 따라서 gamma가 커지면 Overfitting에 가깝게 됩니다.
-
SVM을 구현하기 위하여 사용한 데이터 셋은 Sklearn의 Breast Cancer Dataset이며, 569개의 row와 30개의 Feature로 이루어져있습니다. 대표적인 Classification 용 데이터셋이며, 유방암의 양성 여부를 각 세포들에 대한 정보들(반경, 둘레, 면적 등)으로 분류하는 것이 목적입니다.
1 | |
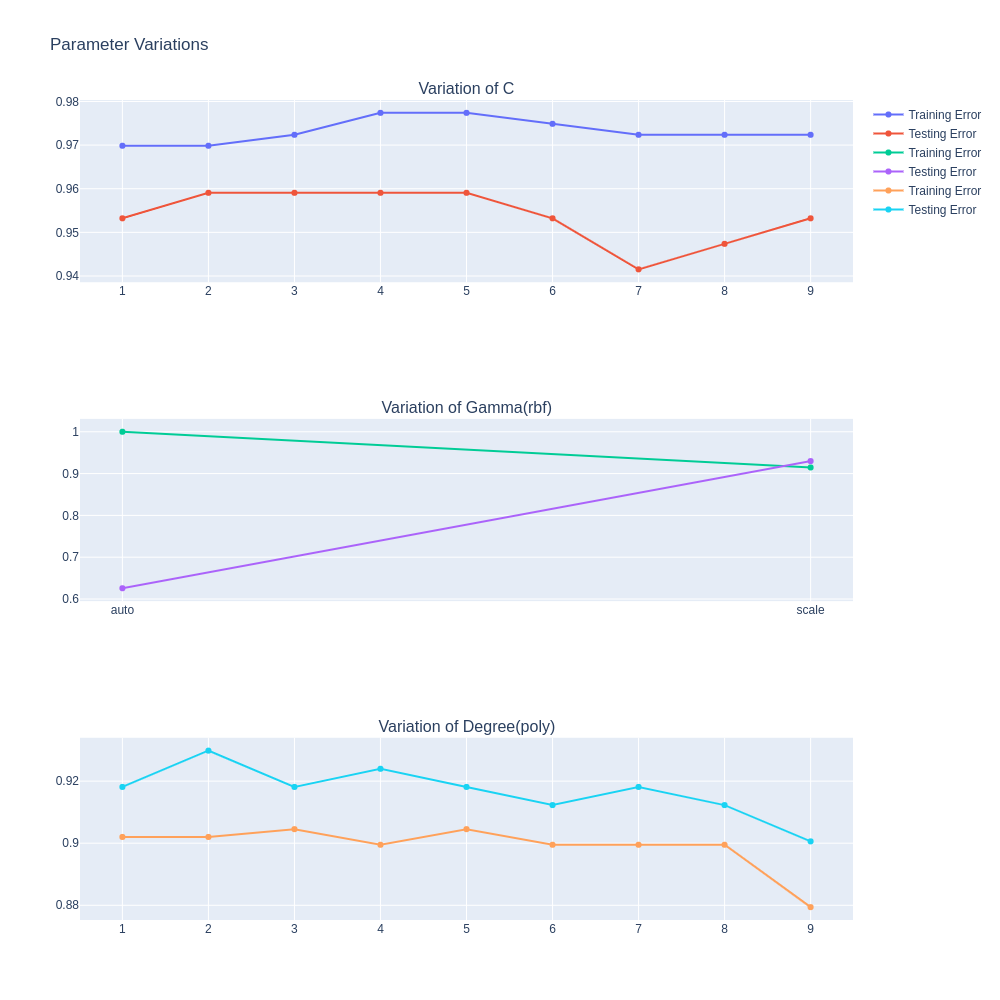
파라미터를 다양하게 바꾼 경우를 리스트업 하자면 다음과 같습니다. 그리고 아래 그림에서 1,2,3번에 대하여 Training Error와 Test Error를 Accuracy로 나타낸 결과를 Plot으로 표현해보았습니다.
-
C parameter (1~10) with {kernel=’linear’}
C Parameter가 증가할수록, Training Accuracy는 조금 증가하나, Test Error는 감소합니다. 이는 Margin의 크기가 점점 줄어들어 Overfitting이 일어났다고 해석할 수 있습니다.
-
Gamma Parameter (‘auto’, ‘scale’) with {kernel=’rbf’}
‘auto’와 ‘scale’의 Train & Test Accuracy 간극을 보면 ‘auto’에서보다 ‘scale’에서 더 좁아, Generalization이 잘 이루어졌다고 할 수 있습니다.
-
Degree Parameter (1~10) with {kernel=’poly’}
차수가 높아질수록, Train & Test Accuracy가 모두 함께, 비슷한 양으로 낮아지는 것을 볼 수 있어, Trade off 대신 전체적인 성능이 낮아지는 것을 관찰할 수 있습니다.
SVR(예측)
다음으로는 SVR을 구축해보았습니다.
SVR을 구축하기 위해 사용한 데이터셋은 Sklearn의 Diabetes Dataset으로서, 사람들의 키, 몸무게와 같은 신상 정보로 당뇨병에 대한 진행도를 예측하는것이 목적입니다.
1 | |
SVR은 같은 SVM기반 예측 모델이기 때문에 SVM과 공유하는 파라미터들이 많지만 epsilon 파라미터를 독자적으로 갖고 있습니다.
-
epsilonfloat, default=0.1
epsilon 파라미터는 SVR 모델의 epsilon tube의 크기와 연관이 있어, 크기가 커진다면 용인하는 에러가 커진다는 뜻입니다. 따라서 값이 커진다면, Penalize하는 에러가 적어지고, 반대로 작아진다면, Penalize하는 에러가 많아지게 됩니다.
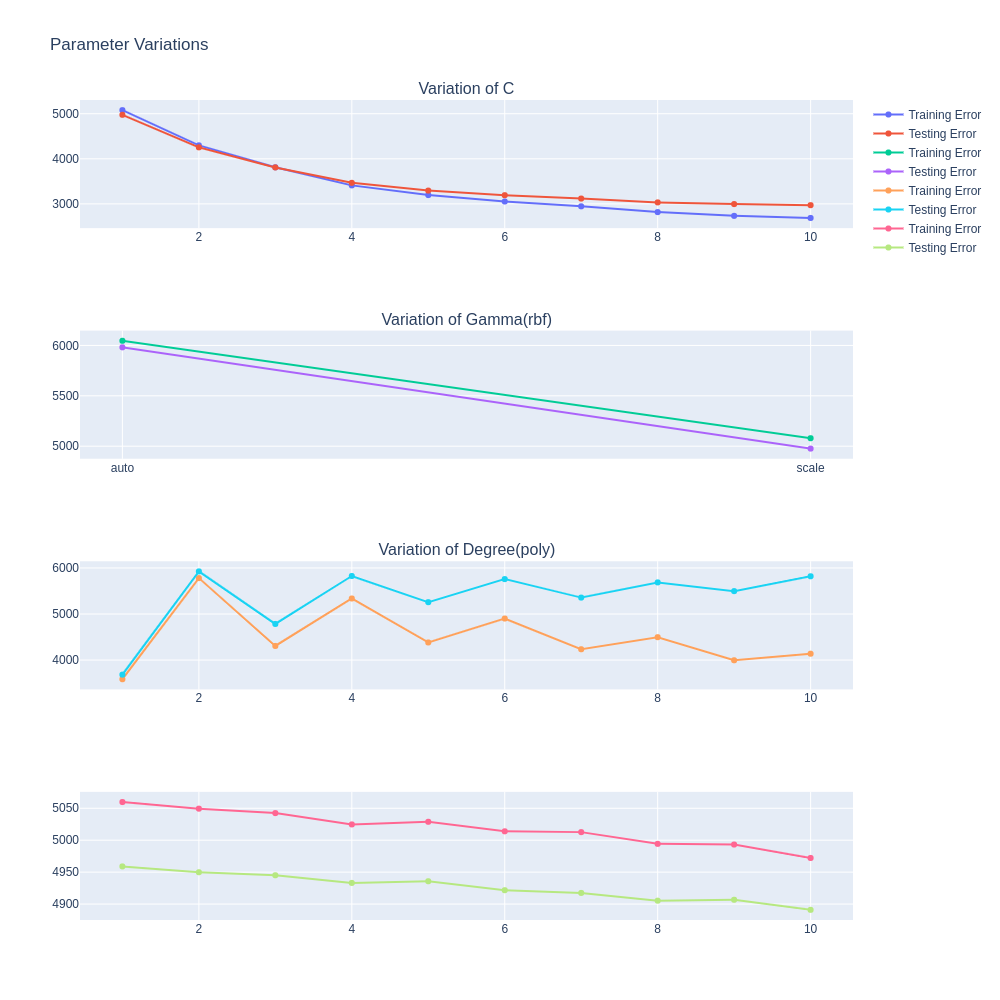
이에 대해서도 Plot을 그려보면 다음과 같습니다.
-
C parameter (1~10) with {kernel=’linear’}
C Parameter가 증가할수록 Loss Function보다 Generalization에 SVR모델이 더 치중하게 됩니다. 이에 따라, Train Error와 Test Error가 큰 간극을 벌리지 않고 같이 감소하는 것을 볼 수 있습니다.
-
Gamma Parameter (‘auto’, ‘scale’) with {kernel=’rbf’}
‘scale’을 사용했을 때 MSE가 더 낮습니다.
-
Degree Parameter (1~10) with {kernel=’poly’}
차수가 높아질수록, Train MSE는 증가, Test MSE는 서서히 감소합니다.
-
Epsilon Parameter(0.1~1)
Epsilon이 증가할수록 Penalize하는 에러가 더 적어지기 때문에, General한 모델이 구축될 것입니다. 따라서 그에 해당하는 Train과 Test Error의 꼴이 나타날 것이라고 예상했지만, Test Error가 전체적으로 낮을 뿐, Train Error에 가까워지는 모습은 보여주지 못했습니다.
(2) Training set과 Testing set으로 나누고 다양한 평가 척도를 이용하여 예측성능을 평가하시오.
다양한 평가 척도를 활용하기 위하여, 같은 조건의 모델을 사용하고 차이점을 관찰하고자 했습니다. 이에 이왕이면 최고의 성능을 보일 수 있는 파라미터 모델로 비교하고 싶어, Bayesian Optimization을 Hyperopt Package로 구현하여 Parzen Window 기법으로 최적화를 진행하였습니다.
이에 따라 Default 파라미터와 Optimal Parameter에 대한 SVM과 SVR의 성능 비교는 다음과 같습니다.
SVM
1 | |
SVR
1 | |
다음으로는, 해당 Optimal Parameter로 다양한 평가척도로 평가를 진행해보겠습니다.
Classification Metric
- accuracy_score
- roc_auc_score
- precision_score
- f1_score
- recall_score
Regression Metric
- max_error
- mean_absolute_error
- mean_squared_error
- r2_score
각 분류와 예측에 대하여 위와 같은 Metric을 선정하였습니다.
1 | |
분류에 대한 Metric같은 경우에는 대부분 비슷한 숫자를 보였기에, 비교의 의미가 크게 없었습니다.
1 | |
하지만 예측에 대한 Metric 같은 경우에는 절대값의 차이가 크게 벌어지며, 특히 R2 Score같은 경우 설명력을 볼 수 있어서 Metric간의 의미 차이가 매우 유의했습니다. 즉 분류를 시행할 때는 Metric에 따른 의미 변화가 크게 없을 수 있지만, 예측 같은 경우에는 어떤 관점으로 데이터 성능을 측정할 지에 따라 Metric의 Variation이 의미가 크다고 생각이 들었습니다.
(3) 다른 분류모델과 비교하여 SVM만의 특징을 기술하시오.
-
다목적 모델
SVM은 같은 개념을 사용하여, 분류와 예측을 둘다 진행할 수 있습니다.
예측에 사용되는 SVM은 특히 Support Vector Regression (SVR)이라고 부릅니다.
SVR과 유사한 목적을 갖는 회귀모델은 Ridge Regression입니다. 따라서, SVR 역시 회귀식을 구성함에 있어서, Robustness를 함께 고려하여 구성합니다.
Ridge Regression Formulation
Ridge Regression의 식을 살펴보면,
$min \frac {1}{2} \sum_{i=1}^n(y_i - f(x_i))^2 + \lambda |w|^2$로 나타낼 수 있습니다. 즉, 실제값과 추정값의 차이를 작도록 훈련하되, 회귀 계수의 크기가 지나치게 커지는 것을 방지하여, Overfitting을 방지하는 것입니다.
SVR Formulation
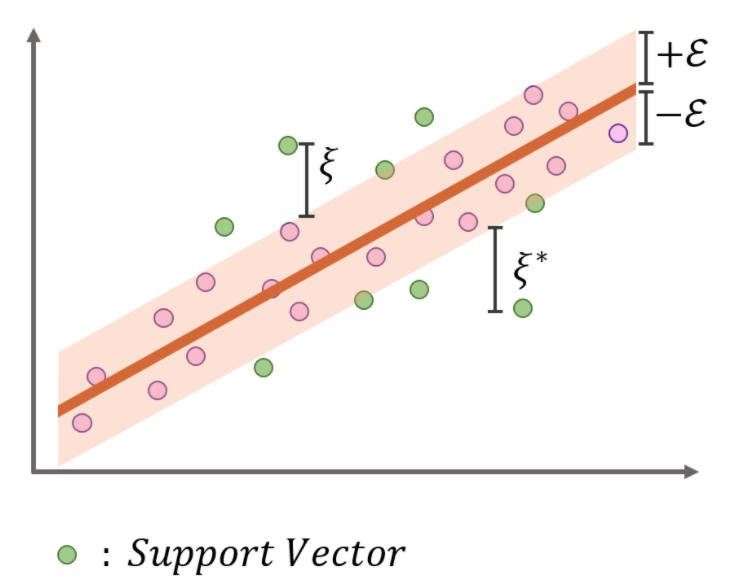
SVR의 식은 다음과 같습니다.
$min \frac {1} {2} |w|^2 + C \sum_{i=1}^n(\xi_i + \xi_i^*)$
이를 읽어보면, Margin은 크게 하면서, 위의 그림에서 음영 처리된 Epsilon Tube를 벗어나는 데이터들에 대해서 Penalty를 최소화 하는 식을 구성하고 있습니다. 따라서 Ridge Regression에서는 식의 앞부분이 Loss, 뒷부분이 Regularization을 담당했던 반면, SVR에서는 반대의 역할을 하고 있는 것을 볼 수 있습니다. Margin을 키우는 것이 정규화를 하는 것으로 생각할 수 있고, $\xi$ 를 줄여나가는 것이 Loss 를 줄이는 것이라고 할 수 있습니다.
-
Train Error & Test Error Simultaneously
보통 머신러닝에서는 training data의 error를 감소시키는 것을 통해 Test Error를 감소시키려고 합니다. 또한 Training Data에만 Overfit하는 것을 방지하기 위해 Regularization 등과 같은 예방책도 포함시킵니다. 이에 따라, Training Error를 감소 시키는 것과 일반화 시키는 것 사이에는 Trade-off가 존재하기 마련입니다.
하지만 SVM은 Train을 하는 과정 자체가 Generalization하는 과정과 같기 때문에 Training Error와 Testing Error를 동시에 줄일 수 있습니다.
-
Kernel Trick
SVM은 머신러닝 기법 중 Kernel Trick을 사용하는 대표적인 기법입니다. 이에 따라 Linear하게 분류 및 예측이 불가능한 데이터에 대해서도 목적을 달성할 수 있으며, Kernel 역시 다양하여 목적에 맞는 Kernel을 파라미터를 수정하며 최적화할 수 있습니다.
(4) KKT conditions에 대해 조사하고 내용을 기술하시오.
KKT Conditions
KKT 조건을 알기 위해선 먼저 Lagrangian과 Duality를 알아야 하기 때문에 서술해보겠습니다.
Lagrangian & Duality
Lagrangian 승수법은 목적식과 제약식이 있을 때, 이 둘을 동시에 활용하여 Optimal Solution을 구하는 방법입니다.
Optimize $f(x)$ ~ objective / utility function
subject to $h_i(x) \leq 0$ for each $ i \in {1, …, m}$ ~inequality constrain functions가 $m$개 존재
$l_j(x) = 0$ for each $j \in {1, …,l}$ ~equality constraint functions가 $l$개 존재
$x \in X$ ~Convex Subsets
즉 위와 같이 목적식 $f(x)$와 inequality 제약식 $g(x)$과 equality 제약식 $h(x)$가 존재할 때, 라그랑지안 Function으로 나타내면 다음과 같습니다.
Primal Problem
Optimize $f(x)$ ~ objective / utility function
subject to $h_i(x) \leq 0$ for each $ i \in {1, …, m}$ ~inequality constrain functions가 $m$개 존재
$l_j(x) = 0$ for each $j \in {1, …,l}$ ~equality constraint functions가 $l$개 존재
$x \in X$ ~Convex Subsets
Lagrangian Primal Function
$L(x, u, v) = f(x) + \sum_{i=1}^m u_i^* h_i(x) + \sum_{j=1}^r v_j^*l_j(x)$
사실 엄밀히 말하자면, Lagrangian approach와 KKT approach는 다른 개념인데, KKT approach는 단순히 Lagrangian의 비선형 최적화를 일반화한 것입니다. 그 이유는 Lagrangian approach는 등식 제약식만을 포함하기 때문입니다. 하지만 이 둘은 보통 혼용하기 때문에 Lagrangian approach라고 서술하겠습니다.
위에서 언급한 Lagrangian Function은 Primal Function입니다. 즉, 궁극적이고 원초적인 목표이며, 이를 풀기 위하여 여러 수단을 사용하는 것이고, 그 수단이 Duality Function입니다.
Duality Function이란,
$g(u,v) = min_x L(x, u, \lambda)$ 입니다. 즉, Primal 문제의 $x$가 최소일 때의 함수이며, 이것을 Maximize하는 것이 목적인 함수입니다.
Lagrangian Dual Function
$g(u,v) = min_x L(x, u, v)$
Lagrangian Dual Function은 Dual Problem과 다릅니다. Dual Function은 Primal을 미분해서 0이 되는 지점이 최소값이므로 해당 변수들($x$)를 다시 Primal Function이 넣는 것입니다.
Lagrangian Dual Problem
이어서, Dual Problem은 Dual Function을 Maximize하는 것이 목적입니다.
$max_{u,v} g(u,v)$
s.t. $u\geq0$
이 때 Dual Problem의 특성으로는
-
항상 Convex하고, $g(u,v)$는 concave하다.
-
Primal과 Dual의 Optimal Value인 $f^$ 와 $g^$ 는 weak duality를 갖는다 = $f^* \geq g^*$
이는 꽤 직관적인 흐름이라고 할 수 있는데 그 이유는, $f^* \geq min_x L(x, u, v) = g^*$ 이기 때문입니다. 즉, Primal Problem의 최소값을 찾는 것은 Dual Problem의 최대값을 찾는 것과 같다는 것을 볼 수 있습니다.
하지만 자세히 보게 되면, 등식이 아니라, 같거나 큰($\geq$) 의미의 부등식입니다. 따라서 작을 수도 있다는 뜻인데 이를 Weak Duality라고 합니다. 이를 완벽하게 같게 하기 위해선 Strong Duality가 필요한데 다음과 같은 조건에 의해서 달성 가능합니다.
-
Slater’s Condition: Primal Problem에서
- 모든 부등제약식이 0보다 작고 $h(x) <0$,
- 모든 등식 제약식이 0과 같을 때, $l(x) = 0$
Strong Duality가 만족하게 되어 $f^* = g^*$를 만족하게 됩니다.
KKT Conditions
KKT conditions, 또는 Kuhn-Tucker Conditions는 같은 개념인데 이름이 다른 이유는 만든 사람들의 순서 때문입니다. 1951년에 Harold W.Kuhn과 Albert W.Tucker가 1951년에 KKT Condition을 발표했지만, 나중에 William Karush라는 사람이 1939년에 이미 박사 논문에 해당 개념을 서술한 것을 발견했기 때문입니다.
KKT Condition에는 네 가지 조건들이 있습니다.
-
Stationarity
최대화 문제: $f(x):\nabla f(x^) - \sum_{i=1}^m \mu_i \nabla g_i (x^) - \sum_{j=1}^l \lambda_j \nabla h_j (x^*) = 0$
최소화 문제: $f(x):\nabla f(x^) + \sum_{i=1}^m \mu_i \nabla g_i (x^) + \sum_{j=1}^l \lambda_j \nabla h_j (x^*) = 0$
$x^$에서 라그랑지안 식으로 바꾼 $L(x, \mu^, v^)$이 최소가 되므로, $x^$일 때 미분값은 0이다.
Feasible의 사전적 뜻은 ‘실현 가능한’이다. 최적화에서 사용하는 뜻은, “제약조건을 만족” 또는 “최적화 문제의 해가 될 수 있는” 이라는 뜻으로서 Primal / Dual Feasibility는, $x$가 $x^*$ 일 때 만족하는 성질을 나타내는 것이다.
-
Primal Feasibility: Primal 제약 조건 만족
$g_i(x^*) \leq 0,$ for $i = 1, …,m $
$h_j (x^*) = 0,$ for $j = 1, …, l$
-
Dual Feasibility: Dual 제약 조건 만족
$\mu_i \geq 0, $for $i = 1, …,m $
-
Complementary Slackness
$\sum_{i=1}^m\mu_ig_i(x^*) = 0$
여기서 만약 $m$이 0이 되면, 부등 제약식이 하나도 없어 사라지게 되므로, KKT 조건은 Lagrange Condition가 되고, KKT 승수는 Lagrange 승수가 된다.
KKT 조건은 명제의 개념이 포함되는데 이에 대한 영어 표현이 익숙하지 않았기에 정리하고 넘어가겠습니다.
-
Necessity(필요조건):
명제 “P $\rightarrow$ Q”일 때, Q는 P가 성립하기 위한 필요조건 명제 P가 참이 되기 위해선, Q가 참일 필요가 있다.
Ex) “인간이면 동물이다” 라는 명제를 두고, [인간 $\rightarrow$ 동물]이라고 설정하면, 인간을 만족하기 위해선 먼저 동물이어야 합니다. 하지만 반대의 경우인, [동물 $\rightarrow$ 인간]의 경우는 말이 되지 않습니다.
-
Sufficiency(충분조건):
명제 “P $\rightarrow$ Q”일 때, P는 Q를 성립하기 위한 충분조건 P가 참이라면, 명제 Q는 참임이 보장된다.
Necessity
KKT Conditions는 두 가지 조건형태를 갖는데 그것이 Necessity와 Sufficiency입니다. 먼저 전자의 형태를 보자면
$x^* / u^, v^$가 primal과 dual solution & Zero Duality $\rightarrow$ $x^* / u^, v^$가 KKT Conditions를 만족한다.
즉, $x, u, v$가 Primal과 Dual의 Optimal Solution이 되고, Zero Duality Gap를 만족하기 위해선, KKT Conditions를 만족해야 합니다.
- $x^$가 $L(x, u^, v^)$를 최소로 만들기 위해선, Stationarity condition에 의해 $\partial L(x, u^, v^)$는 $x^$에서 0이 되어야 합니다.
즉 이 KKT Condition을 만족해야 Zero Duality를 만족한다는 것인데 왜 그런지 살펴보면,
$f(x^) = g(u^, v^*)$
$= min_x f(x) + \sum_{i=1}^m u_i^* h_i(x) + \sum_{j=1}^r v_j^*l_j(x)$
여기서 $\sum_{i=1}^m u_i^* h_i(x) + \sum_{j=1}^r v_j^l_j(x)$ 부분이 Complementary slackness로 인해 모두 0이 되어 $f(x^) = g(u^, v^)$가 달성되므로, Strong Duality를 달성하게 되었습니다.
Sufficiency
$x^* / u^, v^$가 KKT Conditions를 만족한다면 $\rightarrow$ $x^* / u^, v^$는 Primal / Dual Solution이다.
즉, 이번엔 KKT Conditions가 충분조건의 위치에 존재하여, KKT 조건을 만족하면 Primal Dual Solution이 될 수 있음을 나타냅니다.
이를 간단하게 살펴보면,
$g(u^, v^) = min_x f(x) + \sum_{i=1}^m u_i^* h_i(x) + \sum_{j=1}^r v_j^l_j(x) = f(x^)$
애초에 $x, u ,v$ 가 KKT를 만족하니, 이번에도 Complementary Slackness로 인해 $g^$와 $f^$는 동치가 될 것입니다. 이로써 Duality gap이 0이 되어 Strong Duality를 갖기에 Primal Dual Solution이 될 수 있습니다.
Support Vector Machines
위에서 설명한 Lagrangian / Duality / KKT Condition을 어떻게 사용하는지 Support Vector(Hard Margin)을 예시로 설명해보겠습니다.
SVM의 목적은 Margin을 최대화하는 것이며, 이것의 역수를 최소화 하는 문제로 변형시킬 수 있습니다. 이것이 Primal Problem입니다.
-
Objective Function
$min \frac {1} {2} |w|^2$
-
Constraints
s.t. $y_i (w^Tx_i +b) \geq 1$
먼저 목적식과 제약식을 하나의 Lagrangian Primal Function으로 변환합니다.
$L_p(w, b, \alpha_i) = \frac {1}{2} |w|^2 - \sum_{i=1}^N(\alpha(y_i (w^Tx_i + b) - 1))$
그리고 이것을 최소화 하는 것이 바로 Dual Function 입니다.
$min L_{p(w, b)}(w, b, \alpha_i) = \frac {1}{2} |w|^2 - \sum_{i=1}^N(\alpha(y_i (w^Tx_i + b) - 1))$
따라서 $L_p$를 최소화 하는 $w,b$가 필요하므로, KKT의 Stationary를 사용하면 변수들로 편미분을 진행하여 0으로 만들 수 있습니다.
-
$\frac {\partial L_p} {\partial w} = 0 \Rightarrow w = \sum_{i=1}^N \alpha_i y_i x_i$
-
$\frac {\partial L_p} {\partial b} = 0 \Rightarrow \sum_{i=1}^N \alpha_iy_i = 0$
Dual Function은 Primal Function의 Stationary로 구한 변수들 값을 다시 Primal에 집어 넣어 새로운 식을 구성하는 것이며, 이는 다음과 같습니다.
-
Dual Function: $min L_p(w, b, \alpha_i) = \frac {1}{2} |w|^2 - \sum_{i=1}^N(\alpha(y_i (w^Tx_i + b) - 1))$
$=\sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N\sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j$
원래는 Minimization을 구하는 Primal 문제에서 $\alpha$에 대한 식인 Dual 문제는 최고차수가 음수이므로 최대값을 찾는 문제로 변하게 됩니다.
이쯤에서 우리의 원래 구하려는 Solution을 생각해보면, 어떤 $x$가 주어졌을 때, 어떤 Class로 분류되는 것입니다. 따라서 $f(x)$를 만족하는 최적의 식은 $f(x^*)$를 넣어서 구성을 합니다. 이 때 Optimal Value는 위에서 미분으로 구한 $w = \sum_{i=1}^N \alpha_i y_i x_i$입니다.
$f(x) = sign(w^T + b) \Rightarrow sign(\sum_{i=1}^N\alpha y_i x_i^T x + b)$
따라서 해당 식을 풀기 위해선 $\alpha$를 알아야 하는데 이는 KKT Condition의 Complementary Slackness를 통해 나타낼 수 있습니다.
- $\sum_{i=1}^m\mu_ig_i(x^*) = 0$
이는 제약식과 앞의 계수를 곱한 것의 합이 0이라는 뜻이며 이를 Hard-Margin SVM으로 가져오게 된다면, $\alpha_i(y_i (w^Tx_i +b) - 1) = 0$으로 나타나게 되고, $\alpha_i$가 계수 / $y_i (w^Tx_i +b) - 1$ 가 제약식입니다.
그런데 여기에 Dual Feasibility로 인하여, $\alpha \geq$ 0이고, 0인 경우는 w를 0으로 만들어버리니 분류경계면 형성에 영향을 미치지 못합니다. 따라서 $\alpha > 0$을 사용해야하며, 이 때는 $y_i (w^Tx_i +b) - 1) = 0$이므로 Support Vector임을 알 수 있습니다.