CS224W Lecture 5

CS224W 5번째 강의 정리를 정리해보았습니다. 강의에서 사용된 이미지 전체는 CS224W 수업 자료에서 가져왔음을 미리 밝히는 바입니다.

강의 Link: Spectral Clustering

Intruduction

이전 강의에서는 Modularity를 이용한 Graph Clustering 또는 Community Search에 대해 다루었습니다. 이번 강의에서는 Clustering에 있어 다른 관점으로 진행하는 기법을 학습할 것이며, 지금까지의 그래프 논문을 읽고 학습을 한 경험을 미루어보아 Spectral Clustering이 더 많이 관찰되고 사용되었습니다. 즉, 전혀 다른 Partitioning Criteria이고 전도율이라는 새로운 개념으로 Cluster들을 도출해내고자 하며,

• Modularity는 Network의 Physics 관점에서 살펴보려고 하고,
• Conductance는 Computer Science의 Optimization 관점으로 살펴보려고 합니다.

Conductance를 사용하는 해당 기법에서 하고자 하는 질문은

• 그래프 G의 “Good Partition”을 어떻게 정의할 것이냐?
• 효율적으로 Partition을 어떻게 나눌 것인가?

입니다.

Spectral에 대해서 좀 더 이야기해보자면, Graph Convolution 기법과 매우 연관이 크며 이 때 Convolution을 하는 방법 관점에는 Spectral과 Spatial이 존재합니다. Spectral Convolution은 Graph Convolution을 진행함에 있어 Graph Fourier Transform을 사용하고 Frequency의 Spectrum을 사용하여 Filtering을 진행하는데, 이 때 Spectrum이 Spectral이라는 이름과 연관이 크지 않나 추산됩니다.

Three Basic Stages

1. Pre-processing Graph의 Matrix Representation을 구축한다 $\Rightarrow$ Laplacian Matrix로서 노드 간의 관계를 표현한다.
2. Decomposition
   • Matrix의 Eigen value / vector 계산한다.
   • 각 데이터 포인트를 Eigen vector들로써 저차원으로 Mapping 한다.
3. Grouping 각 데이터 포인트를 새로운 representation으로 Cluster에 할당한다.

Graph Partitioning

먼저 Bi-partitioning task; Graph Node를 두 Disjoint group으로 나누는 경우로 살펴봐보겠습니다.

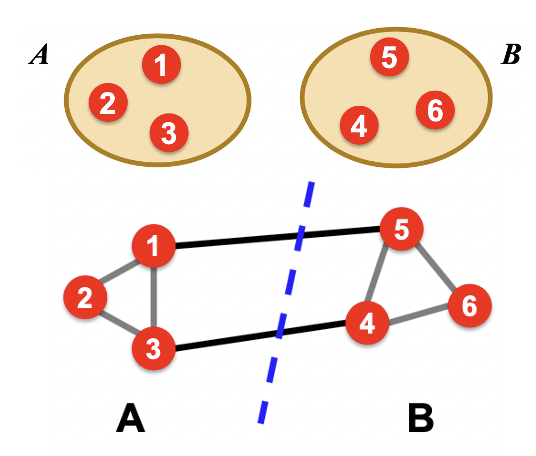
Node가 1~6번 노드까지 존재하고 두 집단 A / B로 나눈다고 했을 때, 위와 같이 표현할 수 있습니다. 그리고 파란 점선이 두 집단을 나누는 선입니다. 이 때 좋은 “Partition”이란,

• Cluster 내의 연결 수가 최대
• Cluster 끼리의 연결 수가 최소

의 구성으로 나타나야 합니다.

Graph Cuts

Graph cut기법은 Partition에 대한 “edge cut”을 하는 것을 말합니다. 즉, Edge로써 Graph cut을 표현하겠다는 것인데 이를 이해하기 위하여 Cut의 정의를 살펴보겠습니다.

Cut: 각 Group끼리 연결되어 있는 Edge Set / $cut(A, B) = \sum\limits_{i\in A, j\in B} w_{ij}$

위의 수식은 Edge의 Endpoint가 모두 A 또는 B로 나타나, 집단 내의 Edge를 표현하는 대신, 집단 끼리의 Edge 개수를 표현하는 것입니다. 따라서 위의 그림을 예시로 살펴보면 A와 B를 잇는 Edge가 2개이고 Unweight Graph라면 모든 Edge Weight가 1이므로 $cut(A,B) = 2$로 나타낼 수 있습니다.

이름으로 느낌을 설명해보자면, 해당 두 집단을 분리하기 위해선 2개의 Edge를 “Cut”해야 한다는 의미입니다. 그렇다면 집단이 잘 분리되어 있다면 집단 간 연결되어 있는 Edge 개수가 적다는 뜻입니다. 따라서 Graph Cut의 Objective는 Cut의 최소화를 추구해야 하며 이를 Minimum-cut이라고 부릅니다. A와 B에 대한 Minimum-cut은 다음과 같이 표현할 수 있습니다.

$arg min_{A,B} cut (A, B)$: Cut A,B를 최소화하는 A,B를 찾자

하지만 이 개념은 문제가 쉽게 발생하게 됩니다.

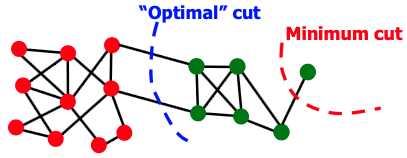
해당 그래프를 Cluster 별로 분할을 하기 위해서 최적의 Cut은 파란색인데, Edge가 적어야 한다는 Cut의 정의에 의하여 빨간 색 Cut으로 나타내버립니다. 따라서 다음의 문제를 안고 있습니다.

Internal Cluster Connectivity를 고려하지 않고, External Cluster Connections만을 고려한다.

Conductance

위의 문제를 해결하기 위하여 새로운 Objective 또는 Criterion인 Conductance를 안내해드리겠습니다. 사전적 정의상 “전도율”이라는 뜻으로서, 두 Cluster간의 전도율이 작아야 좋은 Cluster가 구성된 것입니다. Conductance의 정의는

각 집단의 밀도 대비 Group의 연결 정도

로 표현하여, 분할을 했을 때, 서로의 집단 내에 어느 정도 노드의 개수가 보장이 되어야 한다는 것입니다. 식으로서 나타내면,

$\phi (A, B) = \frac {cut(A, B)} {min(vol(A), vol(B))}, vol(A) = \sum_{i\in A}k_i$

와 같이 표현할 수 있으며, $vol(A)$는 A cluster 내의 노드들의 Weighted Degree와 같습니다. 분모를 ${min(vol(A), vol(B))}$로 나타낸 이유는 두 집단의 균형이 이루어지지 않다면, 둘 중 하나의 Volumn이 매우 작을 것이며 이를 통해 min의 결과가 작고 따라서 Conductance $\phi$가 커질 것이기 때문입니다.

하지만 Conductance cut을 계산해내는 것은 NP-hard라는 문제를 갖고 있으며 이를 위해 Conductance를 근사하고자 합니다. 그것이 바로 Spectral Clustering입니다.

Spectral Graph Partitioning

먼저 Spectral Graph Partitioning (이하 SGP)를 하기 위해선 몇가지 개념을 알고 가야합니다. 쉬운 개념들이지만 이들이 혼합돼 복잡한 관계를 구성합니다.

• Adjacency Matrix: Adjacency Matrix란 Undirected Matrix G에 대하여 정의할 경우, $A_{ij} = 1$이면 두 노드 $i,j$가 연결, 아니면 0으로 나타납니다.
• $x$: $x$는 노드 개수만큼의 vector를 나타내는데, 그래프의 노드들에 대한 Label / Value를 나타냅니다. Label과 Value를 혼용해서 사용하는데 Value로 사용할 경우에는 Feature라고 생각하시면 됩니다.

그렇다면 노드의 인접 여부를 나타내는 A와 노드 Label / Value를 의미하는 $x$와의 연산은 무엇을 의미할까요?

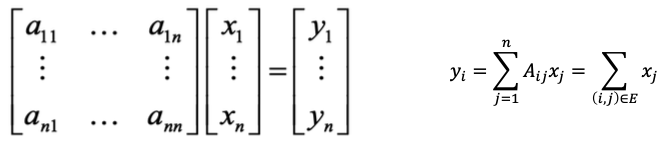
A와 x의 내적을 통해 새로운 y가 도출되었다면, y는 node $i$의 이웃들의 label들을 더한 값들입니다. 즉, 이웃들의 정보를 통해 자신을 표현했다고 할 수 있습니다. 해당 표현을 $x$의 새로운 값으로 설정합니다.

$y_1 = a_{11}x_1 + a_{12}x_2 + … + a_{1n}x_n$

Eigenvector / Eigenvalue view

Spectral Graph Theory는 Introduction에서 설명드린 바와 같이 Graph를 표현하는 Matrix의 Spectrum을 사용하기에 Spectral이라는 이름이 붙여졌으며, Spectrum의 정의는 다음과 같습니다.

Spectrum: Graph의 Eigenvalue $\lambda_i$의 값으로 정렬된 Eigenvector

PCA에서는 Eigenvalue를 내림차순으로 정렬하나 여기서는 오름차순으로 정렬합니다. 그 이유에 대해선 이를 사용하는 방식을 알게 되면 저절로 이해되는 부분입니다.

d-Regular Graph

해당 예시는 최종 결론에 도달하기 위하여 사용되는 예시입니다.

Graph G에 포함된 노드들이 모두 Degree $d$ 를 갖는 상황을 가정해봅시다. 모든 노드의 degree가 같은 경우를 regular graph라고 하기에 d-regular라고 정의내릴 수 있습니다.

다음으로는 G의 Eigenvalue와 vector를 나타내야합니다. G의 구성요소로는 Adjacency Matrix 말고도 Node / Edge Value들이 존재하지만, G의 Eigen값들을 구하기 위해 대표적인 값으로 Adjacency Matrix, A를 사용하겠습니다.

$A\cdot x = \lambda \cdot x$, what is $\lambda$ & $x$

$\lambda, x$의 의미를 파악하기 위하여 먼저 $x = (1,1,1,…1)$의 경우를 살펴보겠습니다. 그렇다면 $A\cdot x = (d,d,d,…,d) = \lambda \cdot x$로 나타낼 수 있기에, $\lambda = d$로 표현할 수 있습니다.

그럼 하나의 Eigen-pair로서 $x = (1,1,1,…,1), \lambda = d$를 구해낼 수 있습니다. 이 때 $d$가 A의 가장 큰 Eigenvalue인데 그 이유에 대해서 강의에서는 설명하지는 않지만, 최강석사가 되기 위하여 한번 살펴보겠습니다.

d가 Eigenvalue 중에서 최강이다

G가 d-regular로 연결되어 있으며, Adjacency A가 정의되어 있을 경우,

• (1) d는 1의 multiplicity를 갖고 있으며, 이 뜻은 d와 연관된 eigenvector는 하나이다.
• (2) d가 A의 Eigenvalue중 최대이다.

Proof:

• Eigenvalue $d$를 얻기 위해선, 모든 노드들의 label / value가 같아야 한다 ($x_i = x_j$)
• 모든 label / value가 같다는 뜻은, $x = c \cdot (1, 1, …,1)$로 표현할 수 있다.
• $S = x_i$의 최대값을 갖는 노드라고 한다면, 모든 노드가 $S$에 포함되지는 않는다. 즉, 모든 노드가 1이라는 균형이 무너졌으므로, 큰 값이 존재하면 작은 값도 존재한다.
• 그렇다면 최대값을 갖는 노드들의 이웃에는 최대값보다 작은 노드값들이 존재할 수 있으므로, $d$보다는 작은 Eigenvalue를 가질 수 있다.
• 따라서, $y$는 Eigenvector가 아니므로, $d$가 가장 큰 Eigenvalue이다.

본 파트는 아직 이해가 조금 부족합니다.

Eigenvalue / Vector 관련하여 조금 짚고 넘어가고 싶은 부분은, 노드들의 Adjacency matrix가 그래프 구조를 대표하는 Matrix라고 했을 때, 해당 행렬의 Eigen-pair는 노드 개수 n만큼 구할 수 있습니다. 따라서 Node 값을 나타내는 Eigenvector가 고정된 값이 아니라 변할 수 있다는 뜻인데, 이 때 해당 벡터가 노드의 Feature라고 한다면, 의미가 조금 이상해집니다. 그 이유는 Feature는 고정되어 있고 가변적인 것은 Label이기 때문이며, 따라서 Label / Value라는 의미를 해당 강의에서는 Label이라고 생각하시는게 좋습니다.

즉, Eigen-pair를 구함으로써 각 노드의 Label을 구해낼 수가 있는데, 이는 결국 그래프의 Feature를 통해 진행하는 것이 아니라, 단순히 그래프 구조만을 보고 나타내는 것입니다.

Example: Graph on 2 Components

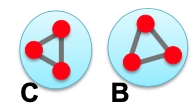
Eigen-pair가 SGP에서 사용되는 원리를 좀 더 살펴보기 위하여 다음과 같이 완전 분할되어 2개의 d-regular Components를 갖는 Graph를 살펴보겠습니다.

위의 $x$ 벡터들에 C Components에 1을 넣는 경우, B Components에 1을 넣는 경우를 나누어 $A\cdot x$의 값을 살펴보면 $\lambda$가 d로 나타나는 것을 볼 수가 있습니다. 이 때 조금 의아할 수도 있는 원인 중 하나는 $x$벡터를 Feature로 이해하는 경우이며 Label이라고 생각해야 계산이 이해가 될 것입니다.

$\lambda$가 $d$라는 뜻은 결국 가질 수 있는 Eigenvalue의 최대값을 가졌다는 뜻인데, 해당 경우에는 Components간의 완벽한 분할이 가능하게 된다는 뜻입니다. 그리고 두 Eigenvector $x’$와 $x’‘$가 다른 값을 가졌지만, Eigenvalue가 같으므로, 두 Cluster가 완벽하게 찢어졌다는 뜻은,

• $\lambda = d$
• $\lambda_n = \lambda_{n-1}$

위와 같은 조건을 만족한다는 뜻입니다. 그리고 위에서 Connected Graph를 살펴보았을 때, Eigenvector가 (1,1,…,1)가 가장 큰 Eigenvalue를 갖는 vector 였는데, Disconnected Graph에서는 불가능합니다. 그 이유는 (1,1,…,1)이 위에서 구한 Eigenvector와 Orthogonal하지 않기 때문입니다.

즉, Eigenvalue가 하나의 Matrix내에서 모두 같다는 뜻은 완전하게 분리되었다는 뜻입니다. 하지만 이를 Connected에 적용하고 모든 노드가 하나의 Cluster로 규정되었을 때의 Vector (1,1,…,1)와 다르게 여러 Cluster로 나누고자 할 때는, 결국 근사를 해야하며, 이는 최대의 Eigen-pair가 아니라 2번째로 큰 Eigen-pair를 사용해야 합니다.

그리고 두 번째 Eigen-pair를 사용해야 하는 이유는 더 있습니다. 가장 큰 Eigenvector는 모두 동일한 Cluster라고 정의하는 (1,1,…,1)인데 이는 두 번째 Eigenvector와 Orthogonal 합니다. 따라서 그 둘의 내적은 0으로 나타나야 하므로, $x_n \cdot x_{n-1}=0$ 로 나타내며, $x_{n-1}$의 벡터의 합이 0이어야 가능합니다.

그럼 Label이 하나의 벡터 내에서 (1/-1)로 표현되는 경우, $x_{n-1}[i] > 0$ vs. $x_{n-1}[i] < 0$ 로 표현되게 되어, 그 둘이 합쳐지면 0으로 계산될 수 있습니다.

하지만 SGP에서 그래프를 대표하는 행렬을 단순하게 Adjacency를 사용하지 않고, 이에 추가적으로 노드의 Degree 정보를 포함한 행렬을 사용하며 이것이 유명한 Laplacian입니다.

Laplacian

Laplacian을 사용하는 이유를 정리해보면 다음과 같습니다.

• 그래프의 꼴을 표현함에 있어, Degree와 Adjacency를 한 번에 표현할 수 있는 행렬

• Positive Semi-Definite 행렬을 만들기 위함이며 해당 행렬은 다음의 특징을 가진다.

  • Symmetric Matrix
  • $n$ real Eigenvalue를 가진다.
  • Eigenvector들이 real-value이며 Orthogonal하다.

  

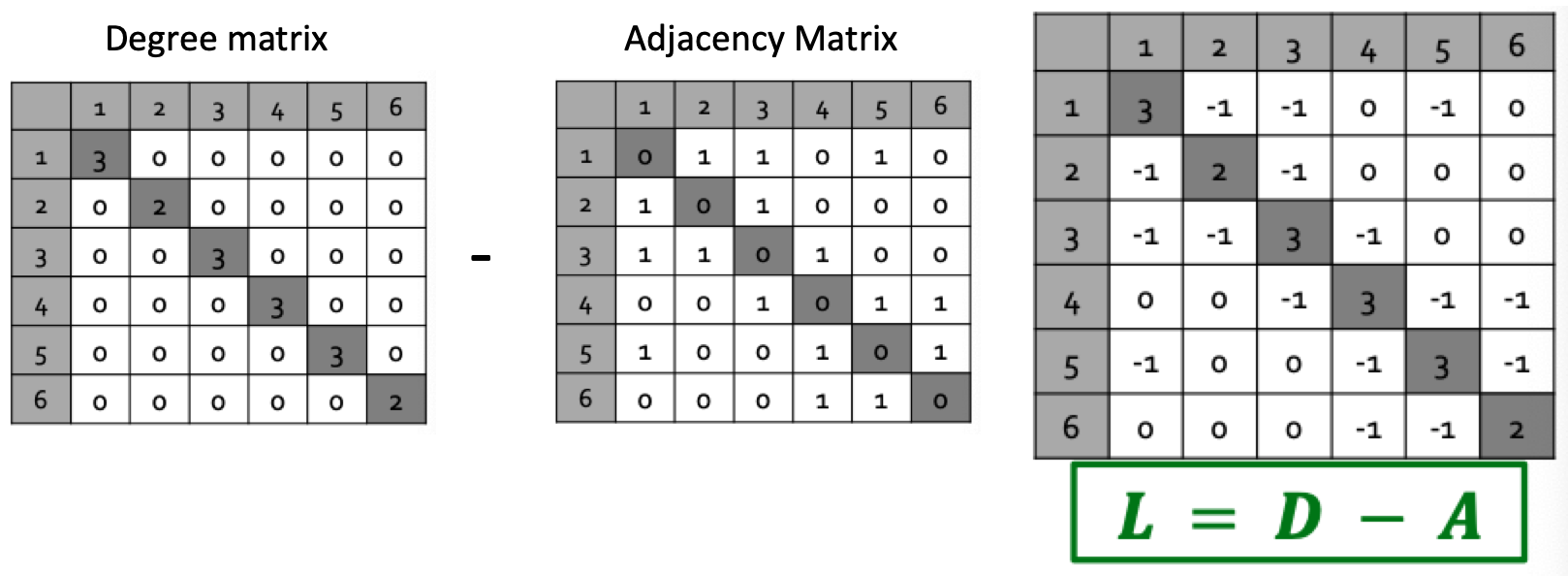
해당 행렬에 곱해지는 $x$ 가 (1,1,…,1)로 나타나게 되면, $L \cdot x = 0$이며 이는 첫번째, 그리고 가장 큰 Eigenvalue가 0이라는 뜻입니다. Eigen value 가 0인 경우를 Trivial Eigenvalue라고 하며, 말 그대로 ‘사소한’ Eigenvalue이니 해당 값은 사용하지 않습니다. 그리고 위에서 살펴본 바와 같이 Clustering Problem에서는 두 번째 Eigen Pair를 찾아야 합니다.

두 번째로 크기가 큰 $\lambda$를 찾기 위한 식은 다음과 같습니다.

$\lambda_2 = min_{x: x^Tw_1 = 0} \frac {x^TLx} {x^Tx}$

해당 식에서 $x^TLx$의 의미는 다음과 같이 표현할 수 있습니다. 즉 $x$ 벡터 내에 있는 Label의 차이를 표현하는 것이며 $x^TLx$의 값이 커질 수록 두 노드의 값의 차이가 크다는 뜻입니다.

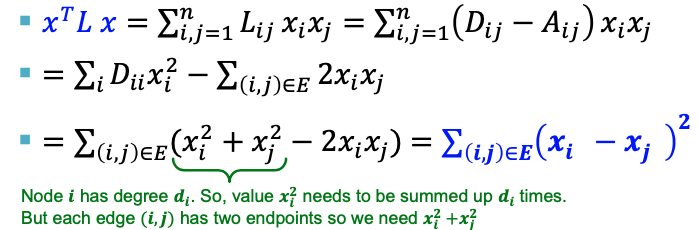
또한 Eigenvector $x$의 특징에 대해서도 정리해야 합니다.

• $x$ 는 Eigenvector이기 때문에 Unit vector이므로, $\sum_i x_i^2 = 1$이다.
• 첫 번째 Eigenvector (1,..,1)와 Orthogonal하기 때문에 $\sum_i x_i \cdot 1 = \sum_i x_i = 0$이다.

정리하자면, 두 번째로 작은 $\lambda_2$를 찾는다는 것은 결국 노드들의 Label의 차이를 최소화 하는 $x$를 찾는 과정입니다. 아래의 식을 Optimize하는 과정은 두 노드 $x_i, x_j$가 값이 다른 경우의 최소화, 즉 두 집단을 가로지르는 Edge가 최소로 나타나도록 최적화 하는 것입니다.

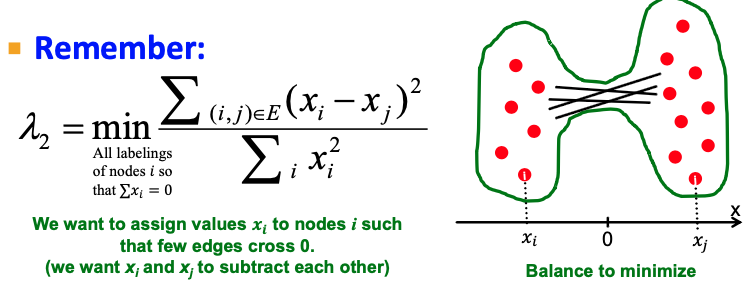
결과

하나의 그래프를 SGP의 절차를 따르게 되면 다음과 같은 그래프들을 얻을 수 있습니다.

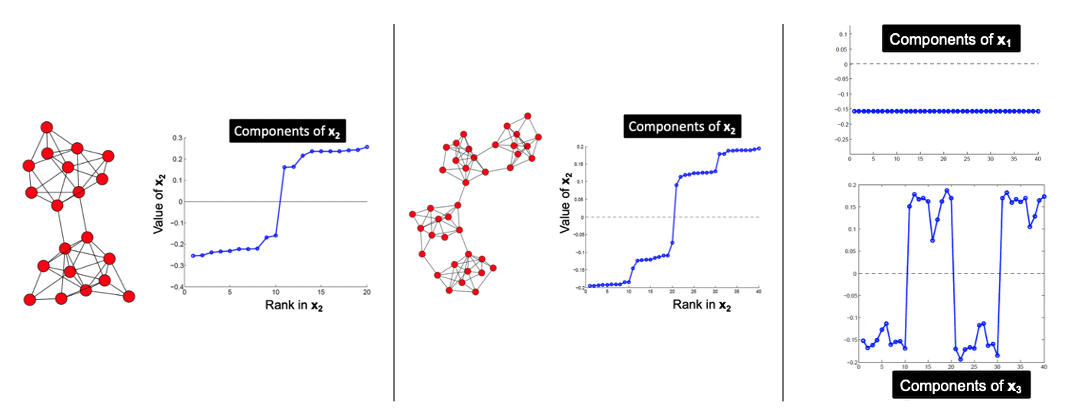
Laplacian Matrix의 Eigen-pair를 구하는 과정이 위와 같은 깔끔한 결론을 낸다는 것 자체가 매우 놀랍다고 생각이 듭니다. 왼쪽의 그래프에서 SGP 결과, 2번째 EigenVector의 값으로 나타나는 $x_2$가 0을 기점으로 양수 / 음수로 나누어짐으로써 Cluster가 정해지는 것을 볼 수 있으며, 중앙의 그림에서는 4개의 Cluster가 분할되는 것을 볼 수 있습니다.

그리고 마지막 그림에서는 $x_1$, 첫번째 Eigenvector가 모두 동일한 상수로 나타나는 것, 그리고 $x_3$도 분할은 할 수 있지만, $x_2$보다는 명확한 분할이 적용 안 된다는 점 등을 파악할 수 있습니다.

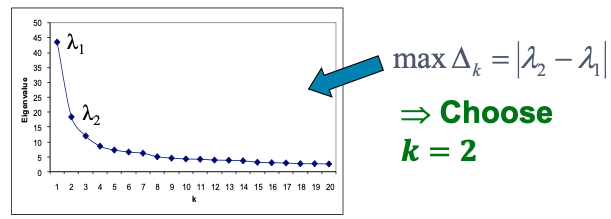
하지만 두 번째 그림에서 예를 들면, 사람들의 관점에 따라 해당 그래프는 4개로 분할 될수도 있지만, 2/3개로도 분할일 가능할 것입니다. 따라서 몇 개의 Cluster로 분할할 것인지에 대한 $k$값 설정이 필요하며 이는 LDA Topic Modeling에서 Topic 개수를 정하는 방식과 유사합니다.