Deep Learning Book Chapter 8

이번 포스트에서는 우리들의 좋은 친구 Ian GoodFellow의 Deep Learning Book Chapter 8, Optimization for Training Deep Models를 정리해보겠습니다. 언제나 그렇듯, 우리 좋은 친구는 매우 많은 내용을 담으려고 하기에 모든 챕터가 매우 난도가 높기에 설명이 부족할 수도 있습니다.

최적화의 종류

Optimization, 한국어로 하면 최적화는 제가 산업경영공학과에 들어오기 전까지는 Gradient Descent를 통해 모델의 파라미터 Space 중 가장 최적의 파라미터를 찾는 것이라고 생각했습니다. 물론 맞는 말이지만 최적화라는 것이 사실 두 가지 종류로 나뉘게 됩니다.

• Numerical Optimization: Train and Error
• Analytic Optimization: Closed Form

지금은 간단하게 Numerical은 Iterative Process를 통해, Analytic은 수식을 정의하고 해결하는 과정을 통해 최적의 파라미터가 나온다고 정의하겠지만, 내용을 정리하면서 좀 더 자세하게 안내하겠습니다.

How Learning Differs from Pure Optimization

진정한(?) Pure 최적화와 머신러닝 / 딥러닝에서 사용하는 최적화는 비슷하지만 다릅니다.

• Pure Optimization: Lagrangian 등과 같은 최적화 식을 구성하여 최대화 / 최소화의 문제를 푸는 방식으로 진행한다. 즉, 비용함수 $J(\theta)$ 자체를 최적화 문제에 맞게 조정하는 것이 목적이다.
• Machine Learning Optimization: 머신러닝은 Performance Metric $P$가 따로 존재하며, 이를 간접적으로 낮추거나 높이기 위하여 $J(\theta)$를 조정한다. 즉 간접적으로 성능을 향상시키려고 하는 것이다.

전형적으로 cost function은 training set Loss Function에 대한 평균으로써 나타낼 수 있습니다.

$J(\theta) = E_{(x,y)\sim\hat p_{data}}L(f(x;\theta), y)$

• $L$: Per example loss function
• $f(x;\theta)$: $x$ input을 넣었을 때 나오는 Predicted Output
• $\hat p_{data}$: Empirical Distribution ~ Empirical이라는 단어가 등장하면, 수중에 갖고 있는 Training Sample을 의미합니다.

위의 식은 결국 Training Set에 대한 Objective Function을 구성한 것이며, 이를 통해 전체 데이터셋에 대한 Loss Function을 근사하려는 목적을 갖고 있습니다. 즉, 본래의 Loss Function이 지향하는 바는 아래의 식으로서

$J^*(\theta) = E_{(x,y)\sim p_{data}}L(f(x;\theta), y)$

• $\hat p_{data}$를 Data Generation Distribution인 $p_{data}$로 치환한 것입니다.

Empirical Risk Minimization

머신러닝의 목표는 예상되는 일반화 오류를 최소화하는 것으로서, 모든 데이터셋에 대해서 완벽한 예측을 하는 것이며, 이 때의 오류를 Risk라고 합니다. 즉, Risk는 $p_{data}$에 대하여 Expectation을 구한 것이라고 할 수 있겠습니다. 물론 $p_{data}$를 수중에 갖고 있다면 해당 최적화 식으로 문제를 풀어내면 끝나는 문제이지만, training dataset 인 $\hat p_{data}$ 밖에 없다면 이를 가지고 근사를 진행해야 합니다. 이 때의 risk를 empirical risk라 하며 이를 최소화하는 것이 ERM이 되는 것입니다. ERM을 통해 전체 데이터셋에 대한 Loss가 최소가 되길 기도할 따름입니다.

하지만 ERM은 다음의 문제를 갖습니다.

• Prone to Overfitting: Training set을 전부 외워버림으로써 가능
• 다수의 유용한 Loss Function이 Gradient의 개념이 포함되어 있지 않다 (e.g 0-1 loss)

이런 이유로 인하여 Deep Learning에서 ERM의 사용은 줄었으며, 최적화의 본 목적에서 살짝 우회해 다른 것을 최적화 시키는 과정 속에서 원래 목적을 최적화시킵니다.

Surrogate Loss Functions and Early Stopping

가끔은 우리가 진정으로 줄이고자 하는 Loss Function이 최적화가 잘 되지 않을 수 있습니다. 예를 들어 0-1 loss는 전형적으로 intractable한데 이 때는 Surrogate Loss Function을 사용하게 됩니다.

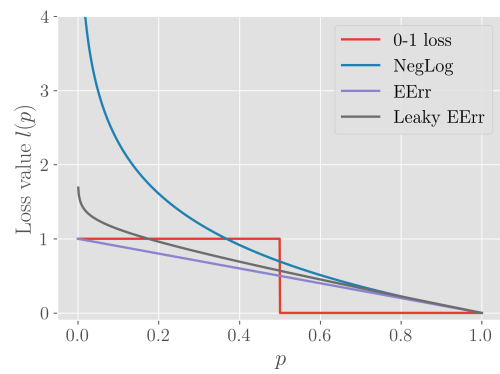
Intractable은 기본적으로 미분이 불가능하여 Gradient를 구할 수 없다는 뜻이며, 이 때 Surrogate Loss Function을 Negative Log Likelihood(NLL)를 사용합니다. 이는 각 Label에 대한 조건부 확률을 구할 수 있으며 이를 통해 Least Classification Error를 구해낼 수 있습니다.

Surrogate Model은 단순히 Intractable한 Loss Function에 대한 대응책이 아니라, 그 보다 더 좋은 효과를 보일 수 있습니다. 그 이유는 0-1 Loss를 통해 Loss가 0이 되었어도, NLL은 더 Generative한 모델을 구축하기 위한 훈련을 추가적으로 진행합니다. 마치 SVM이 Training Error는 0이어도 Margin을 최대한 넓히려고 하는 것과 같습니다.

General한 Optimization과 Training Algorithm Optimization에서의 가장 큰 차이점은 Local Minimum에서 멈추지 않는다는 것입니다. 일반 최적화와 다르게 미리 설정해둔 Early Stopping을 기준으로 Machine Learning의 훈련이 멈추게 되며, 대개 Validation Set Error를 기준으로 설정합니다.

Batch and Minibatch Algorithms

일반 최적화와 머신러닝의 최적화의 차이는 전체 데이터 셋을 사용하는 것이 아니라 Training Example을 분해하여 진행한 다음 더한다는 것입니다. 예를 들어, 다음과 같은 Maximum Likelihood Estimation을 살펴보면 아래와 같은 식으로 표현할 수 있고,

$\Theta_{ML} = arg_\theta max \sum\limits_{i=1}^m log p_{model}(x^{(i)}, y^{(i)};\theta)$

모든 log 확률을 더하는 것을 볼 수 있습니다. 즉, 분해 후 더한다는 것입니다. 이런 분해 후 덧셈은 결국 Training Data에 대한 Expectation을 구하는 것과 마찬가지입니다.

$J(\theta) = E_{x,y \sim \hat p_{data}}log p_{model}(x, y;\theta)$

또한 최적화를 위하여 Gradient를 사용하는 경우에는 모든 Training Data에 대하여 Gradient를 구하여 더해주는 방식을 취합니다.

$\nabla_\theta J(\theta) = E_{x,y \sim \hat p_{data}}\nabla_\theta log p_{model}(x, y;\theta)$

하지만 이는 비용이 매우 높기 때문에, Training Data의 일부 Random Sample에 대하여 Expectation을 구하는 방식으로 진행합니다.

이런 식으로 Random Sample을 사용해도 되는 근간은 다음과 같습니다.

Chapter 5에서 평균에 대한 Standard Error를 살펴봤었으며, 식을 $\sigma /\sqrt n$로 나타났습니다. 이 때 $\sigma$는 sample의 표준 편차, $n$은 Sample 개수입니다. 그렇다면 평균을 구성함에 있어 나타나는 표준 오차는 데이터 개수 n=100 / n=10000을 비교해보았을 때, 10의 Scale 차이밖에 나지가 않습니다. 즉, 데이터 개수가 늘어난다해도 오차의 감소률이 비례하지 않는다는 뜻입니다. 따라서 적은 Sample로도 Gradient를 예측해도 성능의 저하가 크지는 않지만, 이를 여러번 진행함으로써 빠른 Update가 가능하게 되어 Convergance의 속도가 증가합니다.

또한 Training Set에서는 일반적인 경우 중복 데이터가 많이 존재할 것입니다. 극단적인 예시로 모든 데이터가 하나의 데이터로 이루어져 있을 때, Gradient를 단 한번만 계산해도 되는 상황이 생깁니다. 따라서, Random하게 Sample하게 될 경우, Gradient에 영항을 미치는 데이터 분포가 전체 데이터와 유사하게 나타날 것입니다.

용어 정리

• 전체 데이터 셋을 사용하는 알고리즘을 Batch / Deterministic Gradient Methods라고 부른다.
• 단일한 데이터를 통해 업데이트 하는 알고리즘을 Stochastic / Online Methods라고 부른다.
• 중간 지점: Minibatch / Minibatch Stochastic

Minibatch Size 선택 방법

• 큰 Batch Size는 더 정확한 Gradient를 계산하게 해주지만, Linear Return보다는 못하다. Linear Return이란 정확하게는 모르겠지만, Full Batch를 의미하는 것 같습니다.
• 지나치게 작은 Batch Size는 Multicore architecture에서 큰 효용성이 없다.
• Parallel로 Batch가 처리된다면 Batch size에 비례하여 메모리가 사용된다.
• 특정한 Hardware와 어울리는 Batch size가 존재한다. 예를 들어, GPU에서는 2의 제곱승으로 처리되며, 32~256의 사이즈가 적절하다.
• Small Batch Size는 정규화 효과를 갖기도 하는데 Learning Process에 적용되는 Noise 때문인 것으로 사료된다.

다양한 알고리즘들은 Minibatch에서 다양한 종류의 정보를 활용합니다. 어떤 알고리즘들은 Sampling error에 민감하기도 하고, 작은 Batch Size로는 정보를 추출할 수 없는 경우도 존재하지요.

• Gradient만 사용하여 Update를 진행하는 기법들은 Robust한 경우가 많기에 100 정도의 비교적 작은 Batch Size를 사용하는 것이 가능하다.

• Hessian matrix H를 사용하는 경우 $H^{-1}g$를 활용하며, 10000과 같이 더 큰 Batch size 사용해야 하는데,

  gradient $g$에 대한 fluctuation이 다소 존재하기 때문

또한 Minibatch는 Random하게 선택되어야 합니다. 이는 Sample 간의 독립성을 쟁취해 $\Rightarrow$ Sample의 Gradient의 독립성을 취하고 $\Rightarrow$ Minibatch의 Gradient의 독립성을 얻기 위해서입니다. 많은 데이터셋이 ‘순서’를 가진 채로 생성되기 때문에, Shuffle을 통해 이런 순서 및 종속성을 없애는 것이 중요하며 이를 위배 시 모델의 성능에 큰 영향을 미칠 것입니다.

가장 간단한 예시로 교재에서 제시한 예시는 혈액 채취 데이터 셋이 있으며, 1번째 환자에게서 5번, 2번째 환자에게서 3번, 3번째 환자에게서 4번과 같이 Sequential한 특성이 데이터에 반영되면 Sample간의 독립성이 유지되지 못할 것입니다.

Minibatch $\Rightarrow$ Generalization

Minibatch를 사용하여 Gradient Update를 하는 것은 결국 Generalization Error의 Gradient Update를 하는 것을 추구하지만, 이 때 Sample이 반복되지 않아야 하며 이를 통해 Biased 되면 안됩니다. 하지만 대부분의 Implementation은 Training Set의 한계로 인해 여러번의 Training을 단일한 Set으로 진행하여 First Pass 를 제외한 나머지 훈련 시에는 Biased가 되게 됩니다.

따라서 완전하게 Minibatch가 Genearlization의 의미를 갖는 경우는 Online Training, 즉 Data가 꾸준하게 흘러 들어오는 경우입니다. 즉, 한정적인 $(x, y)$가 아니라 Data Generating Distribution인 $p_{data}(x,y)$를 통해 데이터를 받는 경우가 최고라는 뜻입니다. 물론 이런 경우는 흔치 않겠지요.

Challenges in Neural Network Optimization

Optimization은 확실히 어려운 Task입니다. 전통적으로 Objective Function을 Convex하게 바꾸는 것으로 문제를 최대한 줄이려고 노력했으나, 가끔은 Non-convex의 경우를 마주해야할 때가 있습니다. 본 장에서는 Deep Model을 훈련함에 있어 발생할 수 있는 여러 문제에 대해서 살펴보겠습니다.

Ill Conditioning

Convex Function에 대하여 최적화를 진행함에 있어서도 문제가 생길 수 있는데, 이는 Hessian Matrix $H$에 대한 ill-conditioning입니다. Ill-conditioning으로 인해 SGD에서 아주 조그마한 Step을 사용해도 Cost Function이 커질 수도 있습니다.

그 이전에 Ill-condition에 대한 정의를 알아야 합니다. 수치해석 분야에서 함수의 조건수는 argument의 작은 변화의 비율에 대해 함수가 얼마나 변할 수 있는지에 대한 measure입니다. 이 때, 조건수가 매우 크면 Ill-Conditioned / 작으면 Well-Conditioned로서 Ill이라고 표현한 이유는 해당 경우에서 입력의 작은 변화에 Output이 지나치게 변하는 경우는 선호되지 않기 때문입니다.

해당 책의 4장에서도 언급했지만,

$f(x^{(0)} - \epsilon g) \approx f(x^{(0)}) - \epsilon g^Tg + \frac {1}{2} \epsilon^2 g^THg$

와 같이 input에 gradient만큼 제한다음 다시 input으로 활용하는 function의 2차 Taylor 근사는 위의 식과 같습니다. 그런데 Hessian이 Ill-Conditioned 되어, 입력 값에 따라 그 값이 매우 크게 변하는, 즉 곡률이 매우 크게 된다면 자동적으로 Learning Rate는 감소하여 전체적인 훈련 속도를 저해하게 됩니다. 이는 gradient의 경우에는 그 만큼의 변동이 이루어지지 않아 문제가 발생하는 것입니다.

Local Minima

Convex optimization 문제를 푸는 것은 Local Minimum을 찾는 것으로 귀결됩니다. 물론 아래 그림과 같이 Local Minima가 단일하게 나타나지 않는 경우도 있지만, 해당 범위 내에서는 수용 가능한 solution입니다. 즉, Convex Function이라면 local minimum을 찾는 것이 꽤 좋은 솔루션이라는 것입니다.

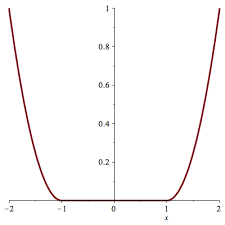
Non-convex function 같은 경우에는 여러 개의 local minima가 존재할 수 있습니다.

해당 파트와 Plateaus 부분은 좀 더 강해져서 설명 드리겠습니다… 아직 무식하여 설명을 못드리겠습니다.

Cliffs and Exploding Gradients

Layer가 많은 Neural Network는 절벽과 같이 Loss Function이 형성되는 경우가 있는데, 이는 큰 수의 Weight가 곱해지는 경우에 발생합니다.

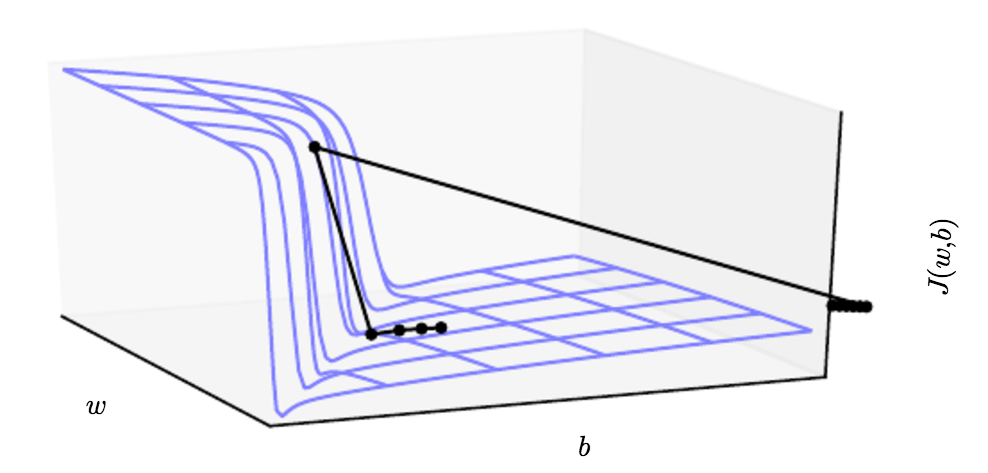
Gradient가 매우 커서 절벽에서 뛰어내리듯이 파라미터들이 크게 급감하거나 증가하게 되면, 지금껏 진행해온 Gradient Update과정의 노력이 증발할 수도 있습니다. 증발이라는 뜻이 다소 의아하게 생각될 수 있는데 제 생각에는 파라미터가 보통 훈련에 있어 1개 이상일텐데, 하나의 Parameter 입장에서는 매우 큰 감소가 이루어져야 할 때, 다른 파라미터는 아닐 수 있기 때문에 바로 절벽에서 뛰어내려버리면 전체의 Gradient Update 밸런스가 무너질 수 있기 때문이라고 생각합니다.

이런 문제를 해결하기 위해서 Gradient Clipping을 사용하는데 기본적인 개념은 Gradient가 지나치게 커서 큰 Step으로 Update가 진행되고자 할 때면, Step Size를 조정하여 천천히 절벽을 내려올 수 있도록 합니다.

아직 저는 무식하여… 전체 다 정리를 못하겠습니다. GoodFellow 형님은 좋은 친구인척 하면서 뒷통수를 치듯이, 쉽다쉽다 하면서 어렵습니다…. 더 강해져서 오겠습니다!