CS224W Lecture 2

CS224W 2번째 강의 정리를 정리해보았습니다. 강의에서 사용된 이미지 전체는 CS224W 수업 자료에서 가져왔음을 미리 밝히는 바입니다.

2번째 강의에서는 Network의 특징을 표현하는 방법, 그리고 Graph를 표현하는 모델에 대하여 살펴보겠습니다.

Network Properties

하나의 Network을 파악하고 다른 Network와 구분할 수 있는 특징들은 다음과 같습니다. 지금부터 설명하는 특징들은 Undirected Graph를 대상으로 나타내는 것이며, Directed Graph에 대해 특별히 설명할 경우 언급하겠습니다.

Degree Distribution, $P(k)$

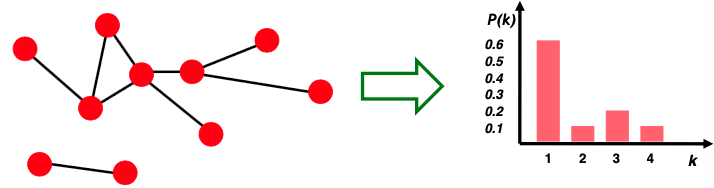
Random하게 선택한 Node가 degree $k$를 가질 확률입니다. Degree는 하나의 노드에 몇개의 Edge가 달려있느냐를 표현합니다.

$N_k$ = 하나의 노드의 Degree $k$

$P(k) = N_k /N$: Normalized Histogram

Directed Graph같은 경우에는 in- / out-degree distribution이 따로 존재합니다.

Path

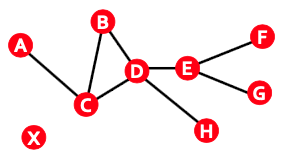
Path는 한 노드에서 다른 노드로 도착하기 위해서 거쳐야 하는 노드들의 Sequence를 말합니다. 다음과 같은 그래프가 있을 때, A와 G의 Path를 계산한다면, 여러 Path가 존재하겠지만 ACBDCDEG와 같이 나타낼 수 있고, 이는 같은 노드를 여러 번 방문할 수 있음을 알 수 있습니다.

• Distance

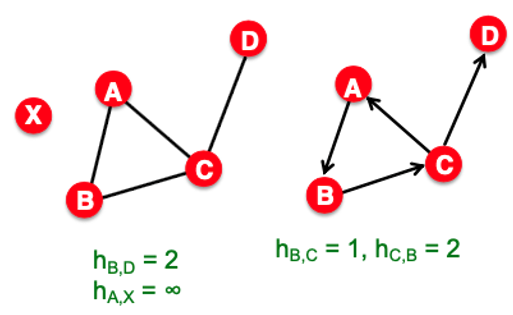
  Path 중에서 가장 짧은 Path를 Distance라고 정의하며, 만일 연결되어 있지 않다면 0이나 무한대로 나타냅니다. 비방향성 그래프는 Distance가 $h_{A,B} / h_{B,A}$가 같지만, 방향성 그래프는 다를 수 있기에 Distance가 대칭의 꼴이 아닙니다.

  

• Diameter

  Diameter는 Distance(shortest path) 중에서 가장 큰 Distance입니다. 최단 거리 중 가장 크다는 뜻은 전체 그래프 사이즈와도 연관이 되기에 Diameter라고 표현한 듯 싶습니다.

• Average Path Length

  Diameter는 최대 Distance를 나타낸 것과 다르게, Average Path Length는 단순히 Distance의 평균을 나타내는 것입니다.

Clustering Coefficient (for undirected graphs)

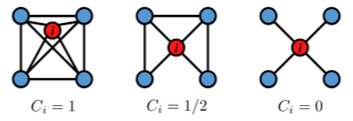
$i$ 번째 노드의 Clustering Coef.란 $i$의 이웃끼리의 연결의 강도를 나타냅니다.

$C_i = \frac {2e_i} {k_i(k_i -1)}$로 나타내게 되며

• $e_i$가 이웃간에 연결된 edge 개수이며,
• $k_i$는 이웃의 개수입니다.

따라서 $k_i(k_i-1)$는 $k_i$개의 노드가 서로를 연결하는 Edge의 최대 개수를 말합니다. 최종적으로 식이 나타내는 의미는 ‘이웃끼리 최대로 연결할 수 있는 Edge에 비해, 현재 연결되어 있는 정도는 얼마냐?’입니다.N개의 노드에 대하여 Average clustering coefficient는 $C = \frac {1}{N} \sum\limits_i^N c_i$입니다.

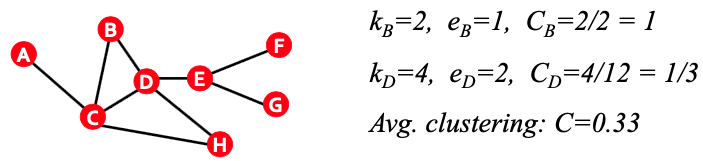
Connectivity

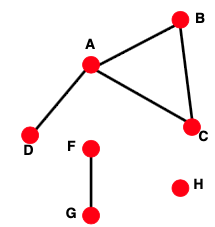
Connectivity는 ‘연결’의 정도를 나타내며, Largest Connected Component라 함은 가장 많은 노드들이 연결되어 있는 그래프라고 할 수 있습니다. 아래의 그림과 같이, ABCD가 묶여 있는 Component가 가장 크다고 할 수 있습니다.

MSN Messenger

지금까지 살펴본 Network의 큰 특징 4가지를 살펴보았습니다. 다음으로는 실제 세계의 Network에서 해당 특징들이 어떻게 나타나는지 살펴볼 것입니다. 원래 이런 예시들은 단순히 예시로만 남는 경우가 있는데, 이번 예시는 뒤의 개념과 이어지기에 언급하고 넘어가도록 하겠습니다.

강의에서 사용하는 예시는 MSN Messenger 사용자들에 대한 예시입니다.

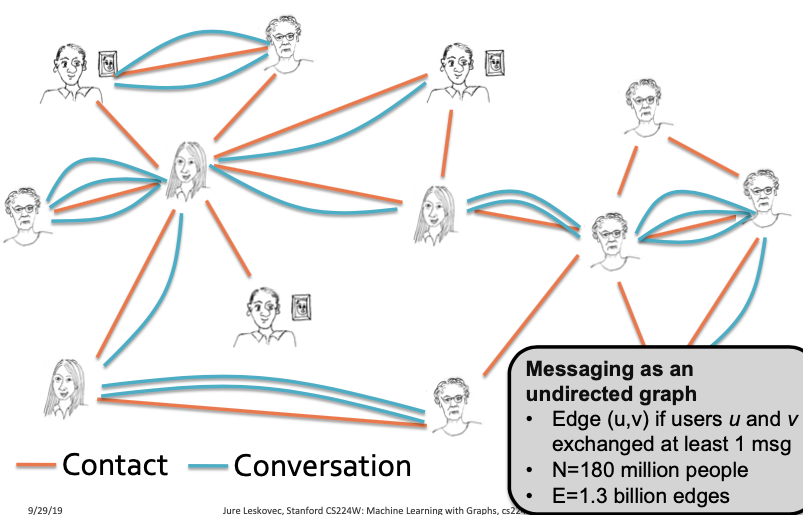
다음과 같이 사람들이 누구에게 메시지를 보내고 대화를 했는지를 Edge로 나타내며, 해당 Network를 구성할 때를 기점으로 한 달 사이에 1개의 메시지라도 보냈으면 Edge로 연결했습니다. 그리고 180 Million의 사람들이 Node로서 나타나고 1.3 billion edge들이 존재합니다.

Degree Distribution

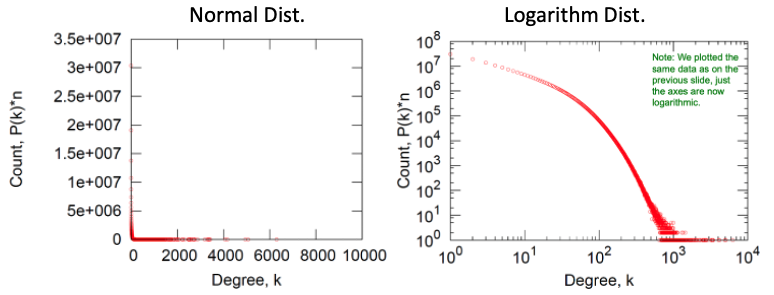
위의 그래프는 Node의 Degree별 Count를 나타낸 그래프입니다. 좌측 그래프를 살펴보면 Degree가 어림잡아 0~200 정도의 Degree를 가진 노드의 빈도가 가장 높으며 그 이상으로 넘어갈 수록 0에 수렵합니다. 우측 그래프는 각 축을 로그 변환하여 나타낸 것인데, 해당 그래프가 Degree가 높아질수록 기하급수적으로 빈도가 낮아지는 양태를 더 잘 보여주고 있습니다.

Clustering Coefficient

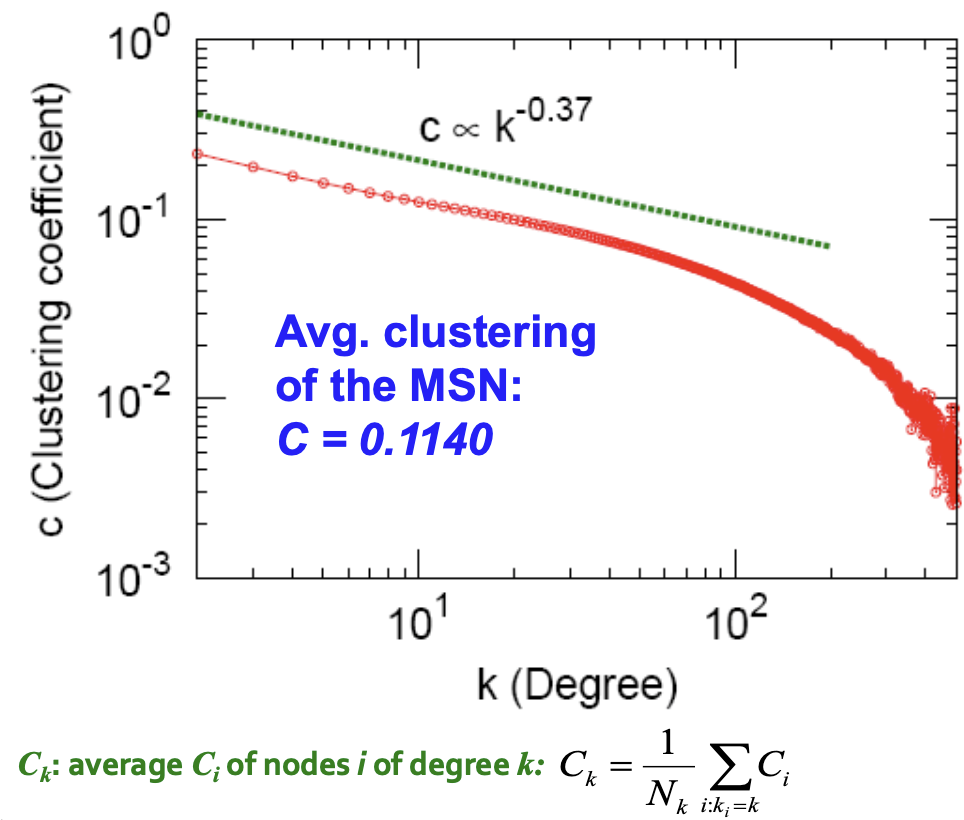
Connected Components

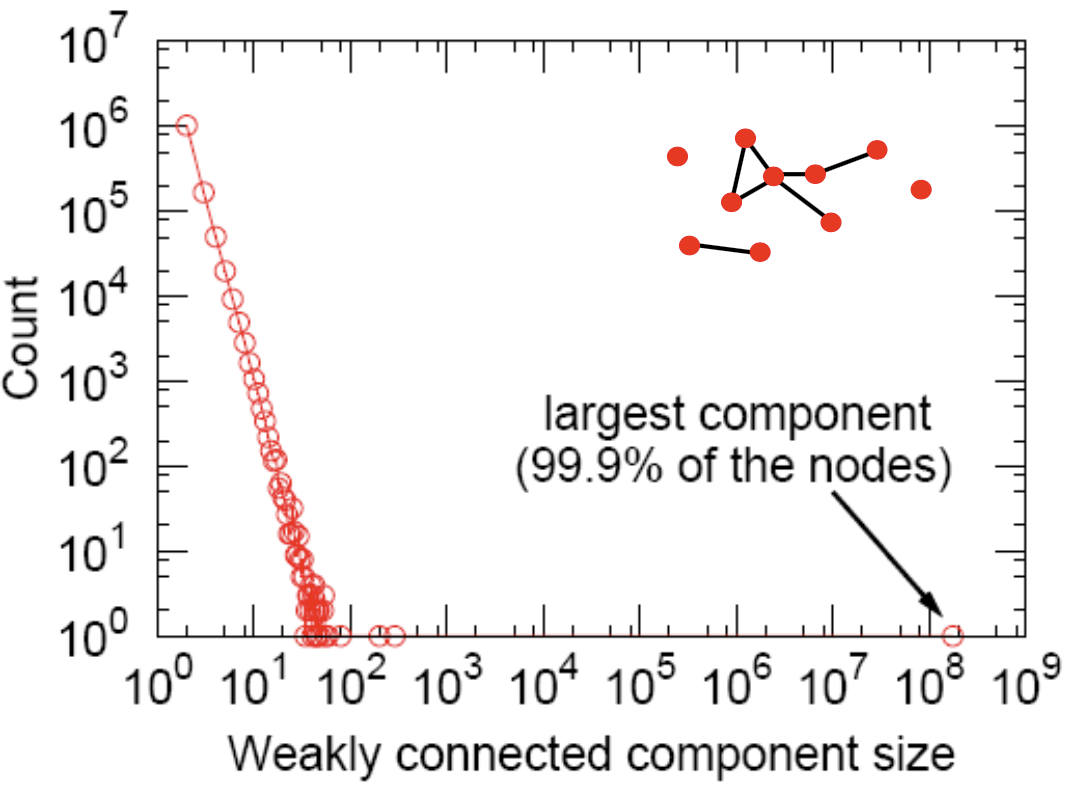
Diameter

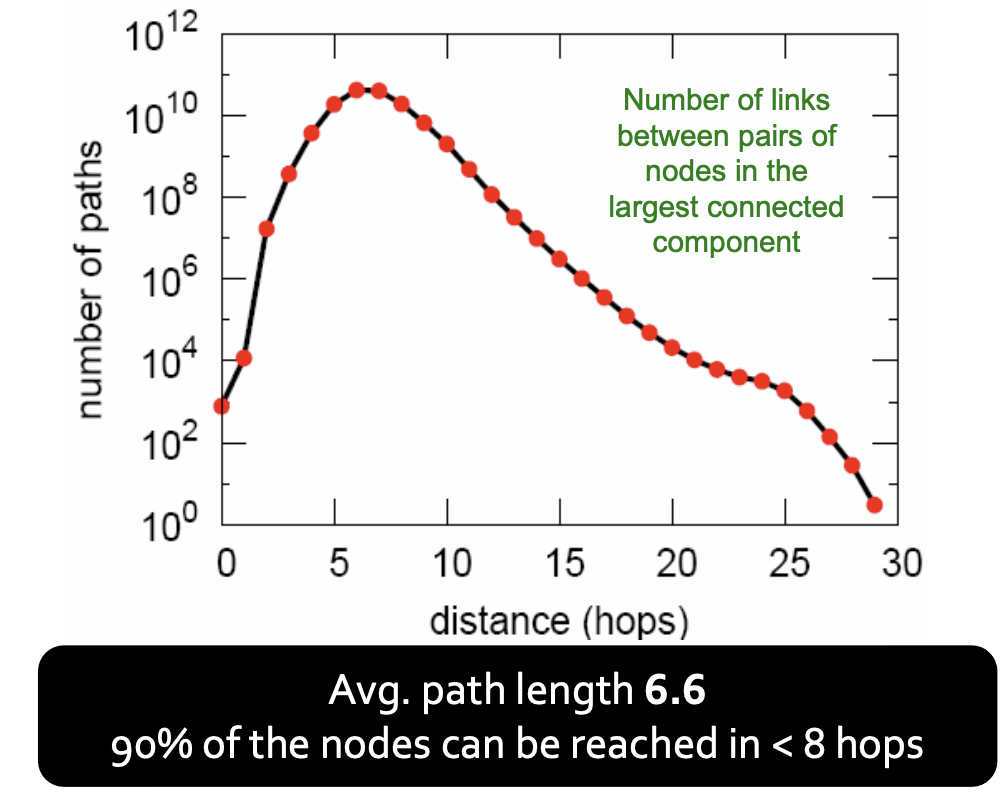
Erdos-Renyi Random Graph Model

위에서 보여드린 예시는 ‘실제 세계’의 Network입니다. 따라서 어떤 System의 Network를 구성하느냐에 따라 Degree Dist. 등과 같은 특징의 양태가 달라질 것입니다. 이에 ‘보편적으로는’ Graph가 어떤 특징을 갖게 될 지에 대하여 모델을 구축한 것이 Random Graph Model이며, 그 중 대표적인 Erdos-Renyi의 모델을 살펴보겠습니다.

해당 모델을 구성하는 데에는 두 가지 Variant가 존재합니다.

• $G_{np}$: undirected graph에서 n개의 노드가 존재하고, 각 edge는 확률 p로 생성된다.
• $G_{nm}$: undirected graph에서 n개의 노드가 존재하고, m개의 edge가 uniform / random으로 생성된다.

강의에서는 $G_{np}$를 통해 모델이 어떤 그래프를 생성해내고, 특징은 어떻게 나타나는지 살펴보았습니다.

본격적으로 특징을 보여드리기에 앞서, n과 p가 동일하더라도 다양한 그래프가 나올 수 있음을 기억하셔야 합니다. n개의 노드는 fix되어있다고 해도 연결을 담당하는 edge가 확률값이기 때문에, 어떤 그래프에서는 두 노드 $(u,v)$가 연결이 되어있을 수도 있고 아닐 수도 있기 때문입니다.

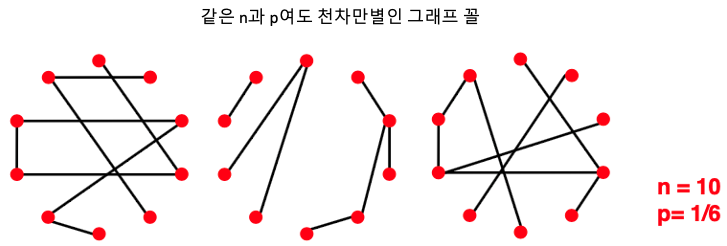
Degree Distribution

Fact: $G_{np}$의 Degree Distribution은 Binomial Distribution이다.

Random Graph Model에서 두 노드가 연결될 확률은 p로 나타납니다. 따라서, 두 노드가 연결이 되냐, 연결이 안되냐 라는 이항분포로 나타낼 수 있습니다. 하나의 노드가 Degree $k$를 갖는 확률은 아래의 식 같이 나타낼 수 있습니다.

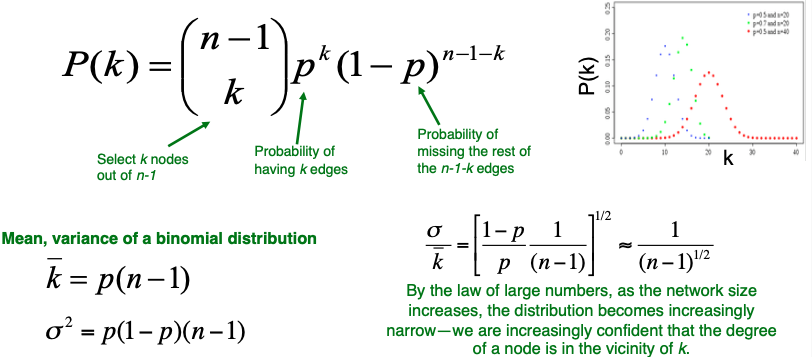
이항 분포의 식으로 확률 분포를 나타낼 수 있고, 따라서 분포의 기대값과 분산을 구해낼 수 있습니다.

위의 그림의 우측 하단을 살펴보면, 분산을 평균에 대한 함수로 나타내는 것을 보실 수 있습니다. 그리고 해당 함수를 전개하게 되면 분모가 $(n-1)$로 나타나게 되는데, 이는 노드 개수가 증가할수록 그래프의 분산이 작아진다는 것을 의미합니다. 분포의 분산이 작아진다는 뜻은 모든 값들이 $k$의 평균값에 근사한다는 말과 동치가 되게 됩니다.

Clustering Coefficient of $G_{np}$

저희는 위에서 $C_i = \frac {2e_i} {k_i(k_i -1)}$ 와 같이 Clustering Coefficient를 나타내는 것을 볼 수 있었습니다.

이때, 분자에 있는 $e_i$는 $i$ 노드의 이웃들간의 edge 개수를 나타내는데, 따라서 이 또한 이항분포의 기대값으로 나타낸다면, $np$의 꼴로 나타내야 하며, $n$ 이 edge의 경우 edge 개수가 $\frac {k_i(k_i-1)} {2}$로 나타낼 수 있기에 위의 식과 같게 됩니다. 그 이후 전체 $C_i$에 대한 식으로 나타내게 되면

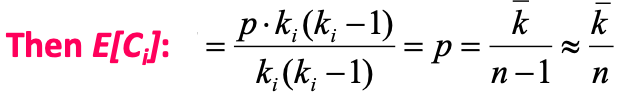
위의 식으로 나타낼 수 있습니다. 해당 식이 나오는 이유는 $k_i$가 고정된 상수이기 때문에 기대값 식 밖으로 빠져나오기 때문이라고 생각하시면 이해가 되실겁니다.

앞에서 degree distribution에 대하여 설명드릴 때, 노드 개수가 증가할수록 분포의 분산이 줄어 모든 노드가 degree $k$를 가질 것이라고 했습니다. 즉, $E[C_i] = \frac {\bar k}{n}$으로 표현될 때, 그래프의 크기가 커질수록 $k$의 평균은 고정일테지만 분모인 노드 개수는 커질 것이며 이는 기대값이 작아지게 만들 것입니다. 따라서 Clustering Coefficient는 감소하여, 하나의 노드의 Neighbor들끼리의 연결 강도가 낮아질 것입니다.

Path Length of $G_{np}$

해당 부분은 다소 난해한 부분이 있었습니다. 새로운 개념인 Expansion $\alpha$가 등장하기 때문입니다.

Expansion $\alpha$

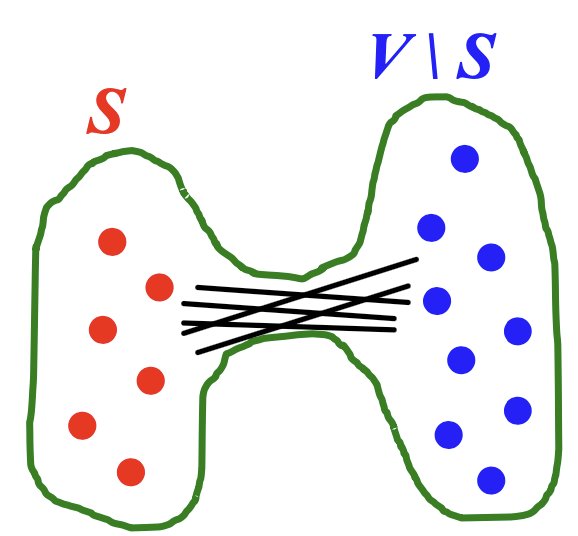
처음 강의를 듣게 되면 흐름과 다소 걸맞지 않게 Expansion이 등장하는데, Expansion이라는 단어 자체의 의미인 ‘확장’이라는 뜻을 곱씹어보면 흐름이 자동적으로 생긴다고 생각합니다. 또한 뒤에서 Random Graph의 크기 (노드의 개수)가 증가할수록 나타나는 변화를 나타내는데, 이를 통해 Random Graph가 점차 증가하는 모습을 Expansion의 가정으로 두어야 합니다. 하지만 기존 그래프에서 노드를 추가한다는 의미라기보다, 전체 Vertex Set V에서 소그룹 S를 분리하고, 해당 S에서 그래프 내의 다른 노드로 확장한다는 의미로 생각하시면 될 것입니다. 마치 Tree꼴의 Graph가 Root에서 BFS / DFS 와 같은 기법으로 뿌리를 내려가는 것과 같습니다. Expansion에 대한 수식은 다음과 같습니다.

$\alpha = min_{S \subseteq V} \frac{# edges\ leaving\ S}{min(|S|, | V - S |)}$

분모의 경우 S 또는 S가 빠진 V 중, 더 작은 것을 고른다고 하는데 이유는 ‘더 작은 것을 골라야 반칙이 아니다?’ 라고 설명하셔서 의미를 잘 파악하지 못하겠습니다. 그 중에서 제가 생각해본 의의는 Expansion이라는 것이 작은 그룹에서 큰 그룹으로 확장을 해야하기 때문에 작은 것을 분모에 포함시키는 것이 아닌가 라는 추측을 남깁니다.

해당 Expansion $\alpha$로 도출해낼 수 있는 Fact는,

Expansion $\alpha$와 $n$개의 노드를 갖는 그래프에서, 한 쌍의 노드는 $O((log \ n) / \alpha)$의 Path length를 갖는다.

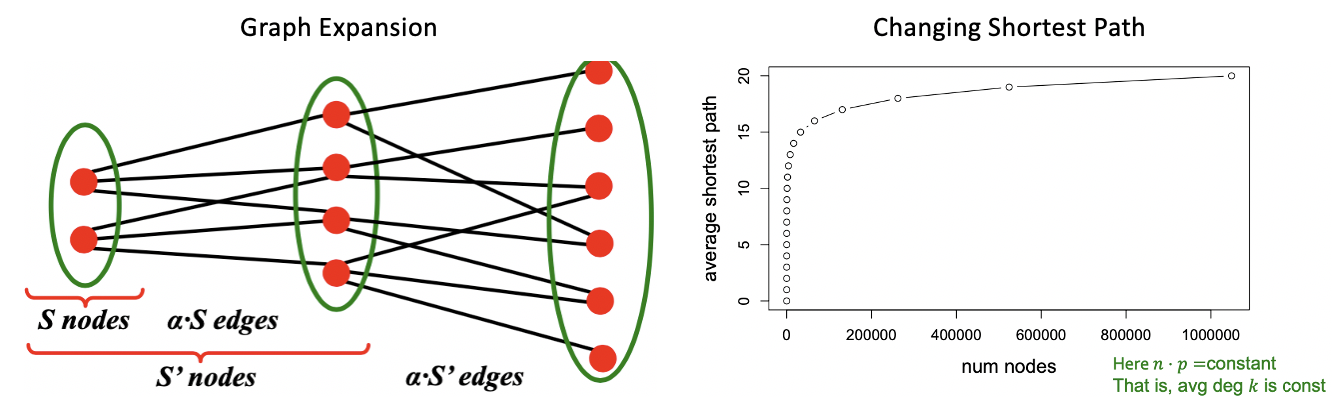
좌측의 그림은 Node 개수가 Expand하면서 Edge 개수도 그만큼 증가하는 모습을 보이고 있습니다. 하지만 우측에서 보이는 Random Graph의 Shortest Path의 변화를 살펴보면, Node 개수가 증가하여 그래프 크기가 커짐에 따라, 그에 해당하는 Shortest Path의 성장은 크게 비례하지 않고 증가 속도가 감소하는 것을 볼 수 있습니다.

Connected components of $G_{np}$

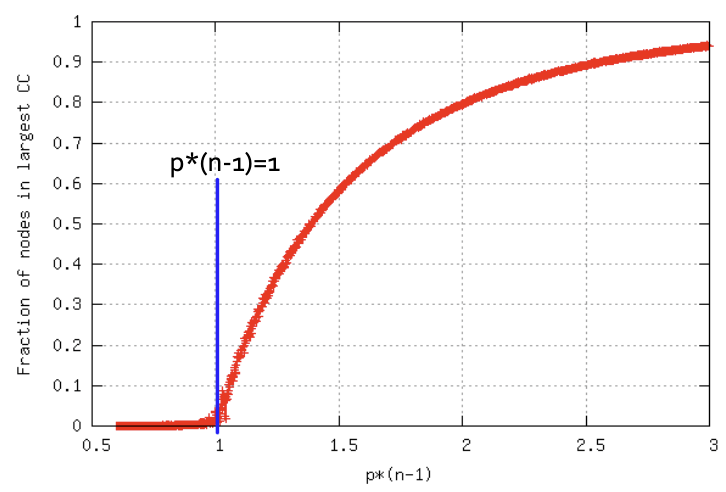
마지막으로 Random Graph $G_{np}$의 Connected Components 중, 가장 큰 크기인 Largest Component가 모든 노드의 Degree가 1 이상일 때 본격적으로 증가하는 특징을 갖고 있습니다. Degree가 2.5쯤 도달했을 때 이미 0.9를 달성하여 거의 모든 노드들이 한 Graph로 이어져있음을 알 수 있습니다. $p*(n-1)$를 Degree로 설정한 이유는 Degree Distribution의 기대값이 곧 모든 노드의 Degree라고 결론을 내렸기 때문입니다.

최종 결과

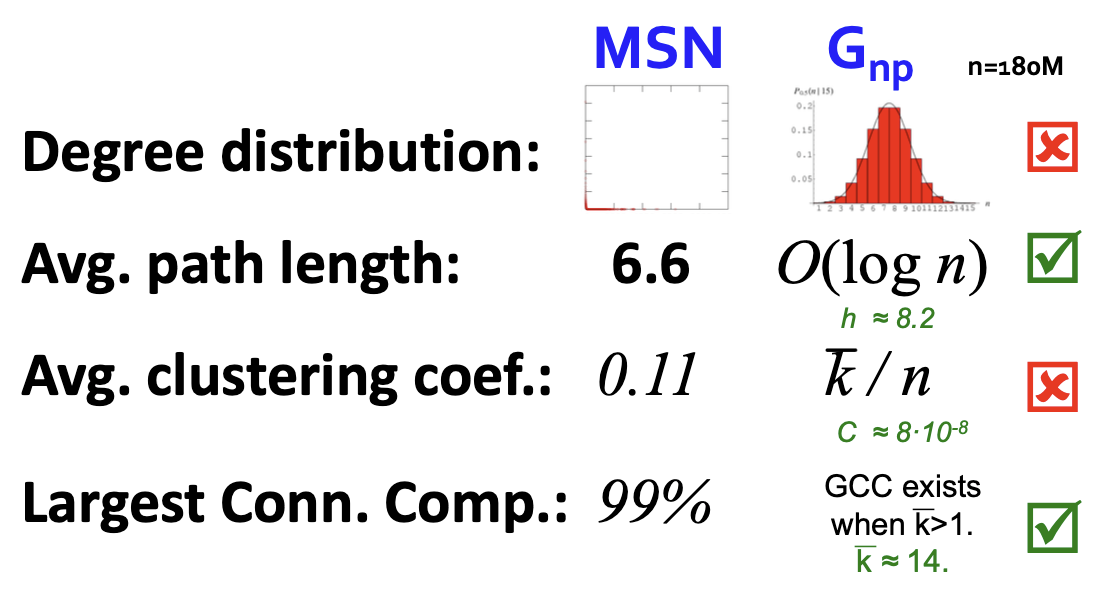
결과적으로 보면 Random Graph와 MSN Messenger를 비교했을 때, 두 가지 특징에서만 같은 결과가 나오게 되었습니다.

• Degree Distribution은 분포 형태가 명확하게 차이나며,
• 평균 Path Length가 6~8로 유사하며,
• Clustering Coefficient는 MSN이 0.11이지만 Model은 0에 가까운 수가 등장하며,
• Largest Component는 $G_{np}$에서 Degree가 1 이상일 때 기하급수적으로 증가하기에 같다고 할 수 있습니다.

따라서 현실의 Network와 Random Network Model의 차이점을 정리해보면 다음과 같습니다.

• Degree Distribution이 Model과 현실의 Network간에 차이가 나며,
• Clustering Coefficient가 모델에서 지나치게 낮아 Local Structure가 존재하지 않습니다.

Random Model과 Real Network가 이렇게 다르면… 뭣하러 배웠나요?

• Random Model은 앞으로 배울 Graph Model의 Reference Model입니다.
• 현실 Network와의 비교를 통해 어떤 Property가 Random Process를 통해 도출이 되었는지 알 수 있습니다.

The Small-World Model

다음으로 살펴볼 모델은 특수한 목적을 갖고 있으며, 이는 “High Clustering Coefficient”와 “Low Diameter”를 갖는 것입니다. 앞의 두 특성을 갖는 그래프는 옹기종기 모여서 소집단을 생성하면서 노드의 최소거리가 크지 않으므로, 작은 세상이라고 할 수 있으며 이를 Small-World Model이라고 합니다. 해당 모델이 실제 Network와의 관련이 크다고 합니다. 먼저 극단적인 예시를 들어보자면 아래 그림과 같습니다.

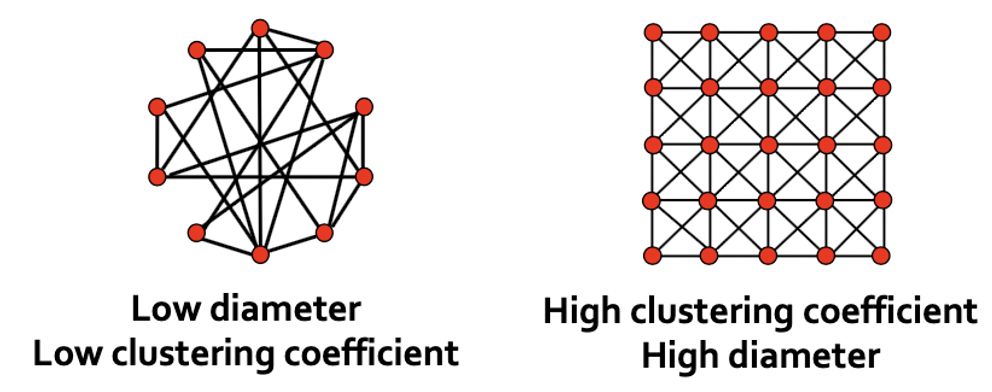
좌측, 우측 모두 Clustering Coefficient와 Diameter가 동시에 크거나 작습니다. 하지만 강의에서 추구하는 Graph 꼴은 SNS와 같이 Clustering Coefficient는 높아 Local Structure도 보존하면서, Diameter도 적어 노드간의 거리가 멀지 않은 것입니다.

이전의 MSN Network와 Random Graph의 Clustering Coefficient를 비교해보면 차수가 7차수나 차이가 나는 것을 볼 수 있었습니다. 그리고 다른 데이터들로 예시를 들어보아도 실제 Network와 노드 개수를 같게 한 채, Random Graph를 그렸을 때, Path Length는 크게 차이가 없지만, 유독 Clustering Coefficient는 작게 나타납니다.

위의 그래프 그림들을 다시 살펴보자면,

• Low Diameter, Low Clustering Coefficient

  Expansion으로 인해 Small Diameter가 나타나는 동시에, Clustering Coefficient.는 작습니다.

• High Diameter, High Clustering

  Triadic closure, 친구의 친구는 내 친구다 라는 이론에 따라 Clustering도 높고 Diameter도 증가하게 됩니다.

하지만 저희가 원하는 Real Network는 Diameter가 작고, Clustering Coefficient가 높으므로 해당 특징에 근사하기 위해 Randomness를 추가하는데 해당 방법을 사용하는 Small World Model의 방법은 다음과 같습니다.

1) 높은 Clustering Coefficient를 가진 Low-dimensional regular lattice(격자)로부터 시작합니다.

2) Randomness(“Shortcuts”)를 적용하는 Rewire를 통해 확률 $p$에 따라 다른 노드에 연결될 수 있도록 합니다.

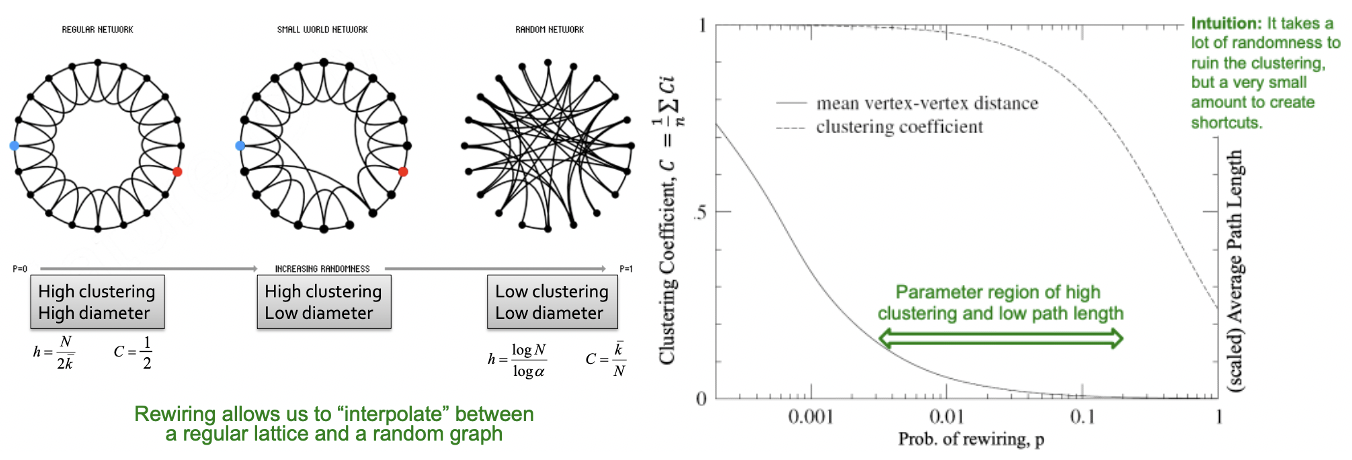
단순한 Randomness를 구현한 Rewiring이 Clustering은 높이고 Diameter를 줄이는 이유는 Regular Network와 Random Network의 중간 지점에 설 수 있기 떄문입니다. 좌측 그림에서 절충선에 서있는 모습을 볼 수 있는데, 우측 그래프를 살펴보게 되면 0.01 정도의 rewiring 확률을 가질 때, 두 마리의 토끼를 모두 잡을 수 있음을 볼 수 있습니다.

물론 처음에 Small-world가 실제 Network를 근사하는데에 용이하다고 말씀드렸지만 과연 그럴까요?

Small World Model은 실제 Network의 High Clustering의 특징을 잘 반영하긴 하지만, Degree Distribution에 대한 설명은 부족하다고 합니다. 따라서 이어지는 Model인 Kronecker Graph Model을 통해 더 큰 Realistic Graph를 생성하는 모델을 살펴보고자 합니다.

Kronecker Graph Model

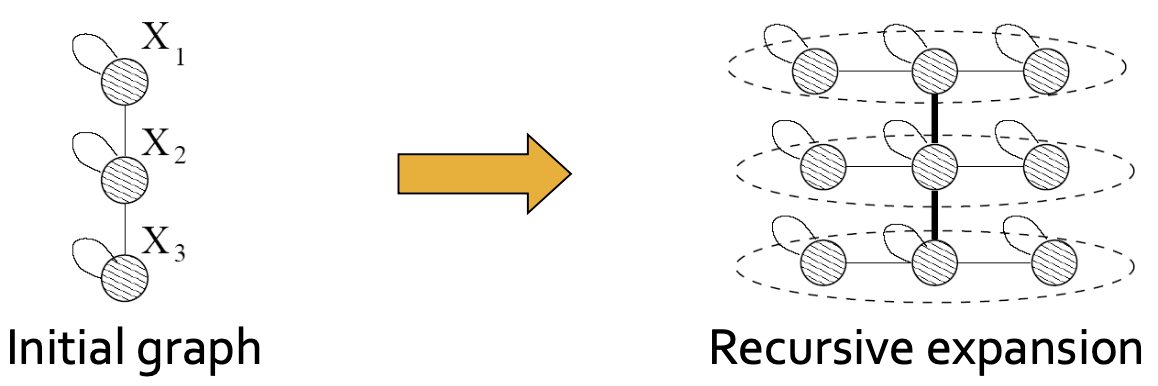
Kronecker Graph Model은 대형 그래프를 구축하기에 적합한 모델입니다. 이에 대한 가정은 ‘Self-similarity’, 즉 비슷한 관계가 그래프 내에 반복적으로 존재한다는 뜻이며 이를 Social Network로 생각해보면, ‘어차피 세상사람들 관계 여러 비슷한 관계들의 집약체이다’라고 정의할 수 있습니다. 즉, 똑같은 Subgraph를 여러 번 재귀적으로 반복하게 되면 빠르게 큰 그래프를 구성할 수 있다는 뜻이며, 아래의 그림과 같이 Initial graph를 Recursive Expansion하여 나타낼 수 있습니다.

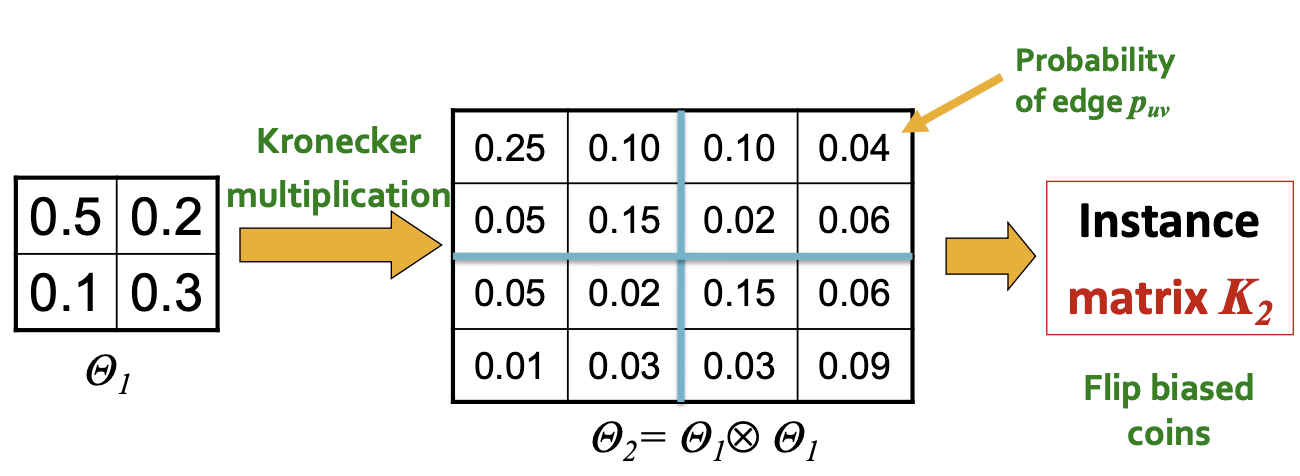
Kronecker Graph Model이라는 이름을 가진 이유는 Kronecker Product가 계산에 포함되기 때문이며, 해당 연산의 꼴은 다음과 같습니다.

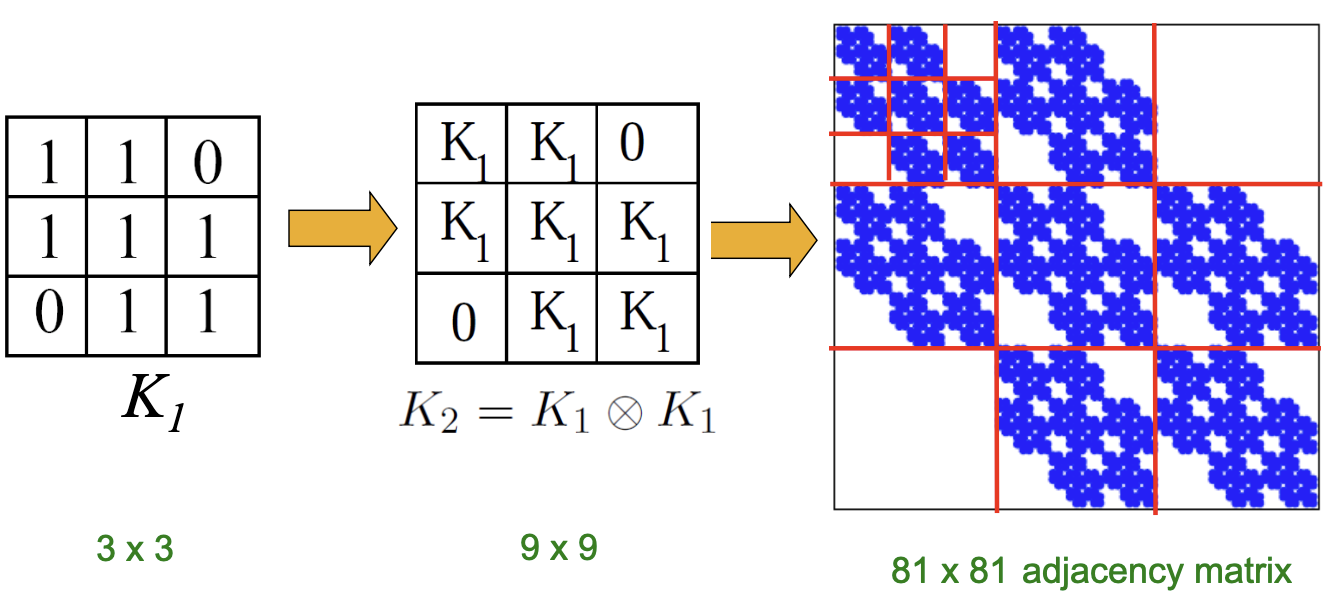
따라서, 하나의 작은 관계가 재귀적인 연산을 거쳐 전체의 큰 그래프를 비슷한 구조로 나타내는 것을 볼 수 있습니다.

위의 예시에서는 모든 Edge가 0/1로 표현되어 있기에, Regular Grid의 꼴과 비슷하게 나타나나 해당 Model은 Real Network를 표현하기에는 부족합니다. 따라서 이를 보완하기 위하여 각 Edge가 발생할지에 대한 여부를 확률, 즉 Stochastic에 표현하는 것을 통해 Generalization을 진행하는 것이 필요합니다. 이는 아래와 같이 단순히 Adjacency Matrix를 확률로 표현해 해당 확률로 Edge가 발생할 것임을 나타낸 뒤, Kronecker Matrix를 생성하는 것으로 이루어집니다. 행렬 안의 확률은 더해서 1로 나타나지 않아도 되는 것이 각 개별적인 Edge의 발생확률이기 때문입니다.