CS224W 3번째 강의 정리를 정리해보았습니다. 강의에서 사용된 이미지 전체는 CS224W 수업 자료에서 가져왔음을 미리 밝히는 바입니다.

3번째 강의에서는 하나의 Graph 내에 존재하는 하위 그래프에 대해서 설명하며, 이를 표현하기 위한 Motif / Graphlets를 설명합니다.

또한 Graph내에서 노드들이 갖는 Role에 대해서도 설명합니다.

Subnetworks

Subnetworks란 하나의 network를 구성하기 위한 ‘Building Block’이라고 생각하시면 됩니다. 이는 아래의 그림과 같이 전체 그래프를 구성함에 있어, 노란색의 하위 그래프들이 사용된다는 것입니다. 예를 들어, 레고로 공룡을 만든다고 했을 때 노란 Block을 많이 사용하면 노란 공룡이, 초록색을 많이 사용하면 초록 공룡이 되는 것처럼 Graph도 사용하는 Subgraph에 따라 그 성격이 달라지게 됩니다. 따라서 Network을 서로 구분할 때 활용할 수도 있습니다.

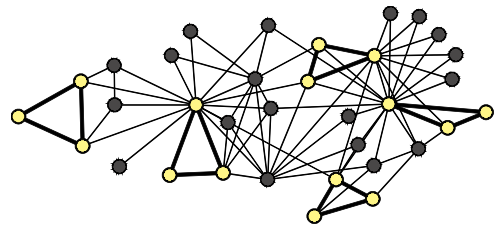
Subgraph 예시

Subgraph의 예를 살펴보면 다음과 같습니다. 아래의 예시는 Node가 3개로 이루어진 그래프(Directed)에 대하여 꼴이 같지 않은(Isomorphic) 일련의 Subgraph들입니다. Node와 Edge가 같으면 Isomorphic이지만, 본 케이스에서는 연결된 Edge의 방향이 모두 개별적이니 꼴이 다르다고 표현합니다.

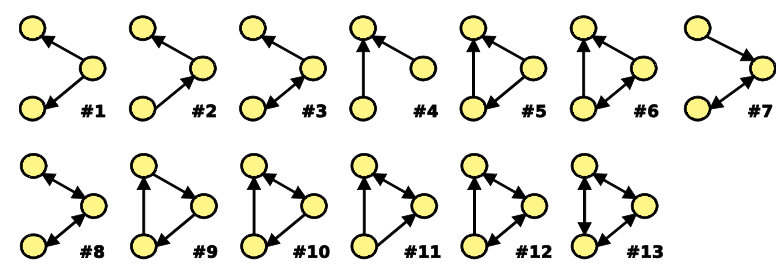
위에서 어떤 Subgraph가 Graph내에 존재하는지에 따라 전체 Graph 성격이 달라진다고 말씀드렸습니다. 즉, Graph내의 특정 꼴의 Subgraph의 중요도를 파악함으로써, 두 개의 그래프를 비교할 때, 한 그래프는 #1번 유형의 Subgraph가 중요도가 높고, 다른 그래프는 #3번 유형의 Subgraph의 중요도가 높다는 것으로 특징 지을 수 있습니다. 이 때, 중요도인 Significance는,

Negative Significance: Under Representation
Positive Significance: Over Representation

로서 나타낼 수 있습니다. 그리고 이 Significance를 모든 Subgraph 유형에 따라 Vector로 나열한다면 “Network Significance Profile” 로서 표현할 수 있습니다.

Subgraph Type	#1	#2	#3	#4	#5	#6	#7	#8	…
Significance	0.12	0.04	0.001	0.25	0.033	0.00742	0.1	0.009

이런 Profile을 통해 Network별 특징을 나타낼 수 있는 방법의 예시는 다음과 같습니다.

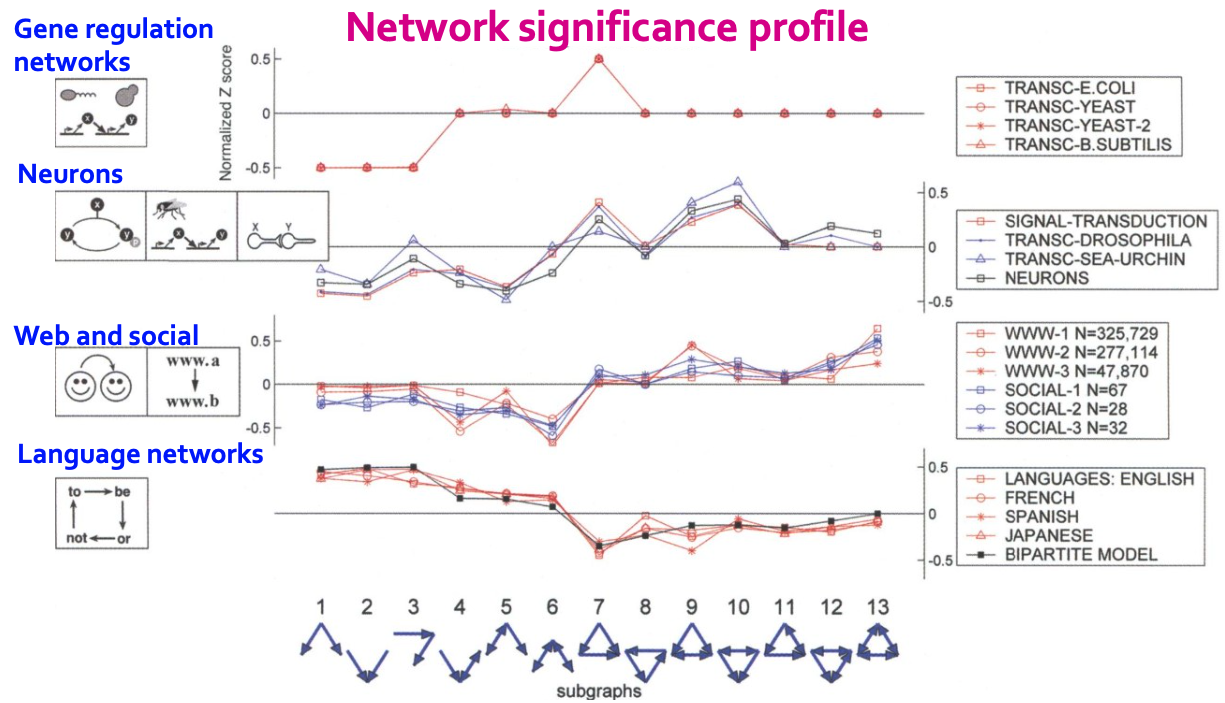
위의 그림에서는 Web / Neuron / Language등과 같이 각양각색의 Network를 보여주고 있습니다. 그리고 Network의 종류별로 각 Subgraph Significance로 나타낸 Significance Profile이 다르게 나타나는 것을 볼 수 있습니다. 하지만 유심히 보아야 할 점은 Inter-Graph Similarity는 낮지만, Intra-Graph Similarity는 높다, 즉 같은 Graph 종류 내에서는 Profile의 꼴이 같다는 것입니다. 예를 들어 마지막 Language Network를 살펴보면, 결국 모두 언어의 특징을 반영하고 있는 Network들이기 때문에 비슷한 성격의 Subgraph의 강도가 비슷하게 나타남을 알 수 있습니다.

Subgraphs, Motifs, and Graphlets

Network Motifs란 무엇일까요? 저는 사전적 정의를 살펴보기 이전에는 이를 Motive와 관련된 단어로서, 모티브라는 말이 “동기”라는 뜻이기에 Network의 근원이라는 뜻이라고 이해했습니다. 하지만, 물론 크게 벗어나는 뜻은 아니지만 Motif라는 것이 원래 생물 분야에서 등장하는 말이며 자세히는 모르겠지만, DNA 염기서열이라고 함으로, ‘근간’ / ‘Base’ 정도로 아시면 좋을 것 같습니다.

지금까지 말했던 것은 ‘사전적 정의’이며, Network에서는 “Recurring, Significant patterns of interconnections”라고 합니다. 따라서, 해당 정의의 구성요소를 하나씩 살펴보면,

Pattern: Small Induced Subgraph로서, 전체 그래프 내의 Vertex와 Edge들을 토대로 일부를 사용하여 도출해낸 Subgraph입니다.
Recurring: 높은 빈도로 반복적으로 나타났다는 의미입니다.
Significant: Random Graph에서 발생할 빈도보다 많이 등장했다는 뜻입니다. 통계의 유의성 검증을 할 때 사용하는 개념인 ‘우연으로 사건이 발생할 확률보다 높다’의 느낌과 비슷합니다.

Motif는 결국 Subgraph를 좀 더 구체적으로 나타낸 것이라고 할 수 있으며, Subgraph들 중 일정한 패턴으로 나타나기에 “이 정도는 기억해두고 정의해두자”라는 느낌이 강합니다. 강의에서는 3가지 예시만 들지만 이를 포함한 더욱 다양한 Motif는 아래의 그림과 같으며, Motif의 특성에 대하여 하나씩 살펴보겠습니다.

Pattern: Induced Subgraphs

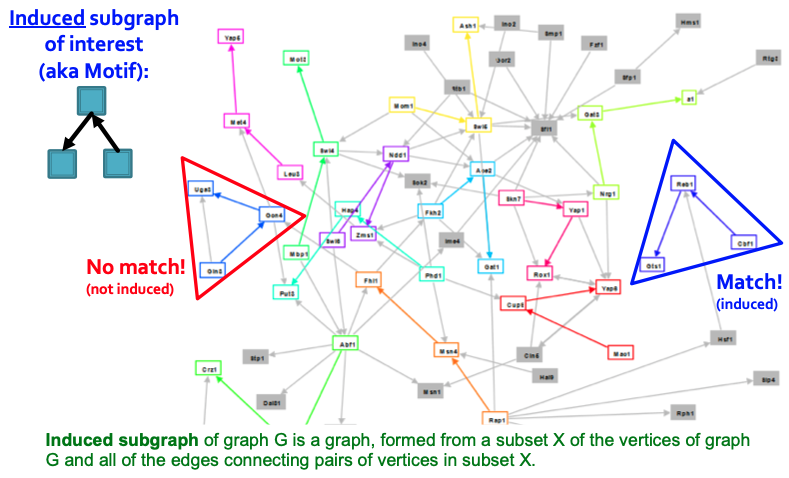
Motif의 개념이 다소 헷갈리는 부분이 있기에 다음의 예시를 살펴보겠습니다. 아래 그림에서 좌측에 Motif가 나타나있고, 우측에는 전체 그래프가 있습니다. 전체 그래프의 특성을 정의하기 위하여 Subgraph를 찾아야 하는데 이 때 좌측의 ‘자주 나타나는 Subgraph 종류’인 Motif가 있는 것입니다.

처음에 아래의 예시를 살펴보고 헷갈렸던 부분은 빨간 삼각형과 파란 삼각형에서 모두 Motif와 일치하는 것 아닌가였습니다. 하지만 강의자가 옳았으며 이유를 설명드리겠습니다. Motif는 Induced Graph입니다. 따라서 해당 정의를 Wikipedia를 통해 좀 더 확실히 나타내면,

전체 $G = (V, E)$ 그래프가 있을 때, $G$의 Vertex의 Subset이 갖고 있는 Edge들로 통해 구성한 그래프

입니다. 즉, Subgraph를 정의함에 있어서 순서를 굳이 정하자면 Node를 먼저 선택한 뒤, 갖고 있는 Edge를 연결하는 것입니다. 하지만 빨간 삼각형에서는 Node 세개를 고르면 회색으로 표시된 Edge가 자동으로 같이 정의되기에 삼각형의 꼴이 나타나지만, 파란색에서는 두 개의 Edge만 정의되기 때문에 Match입니다.

Recurrence: High Frequency

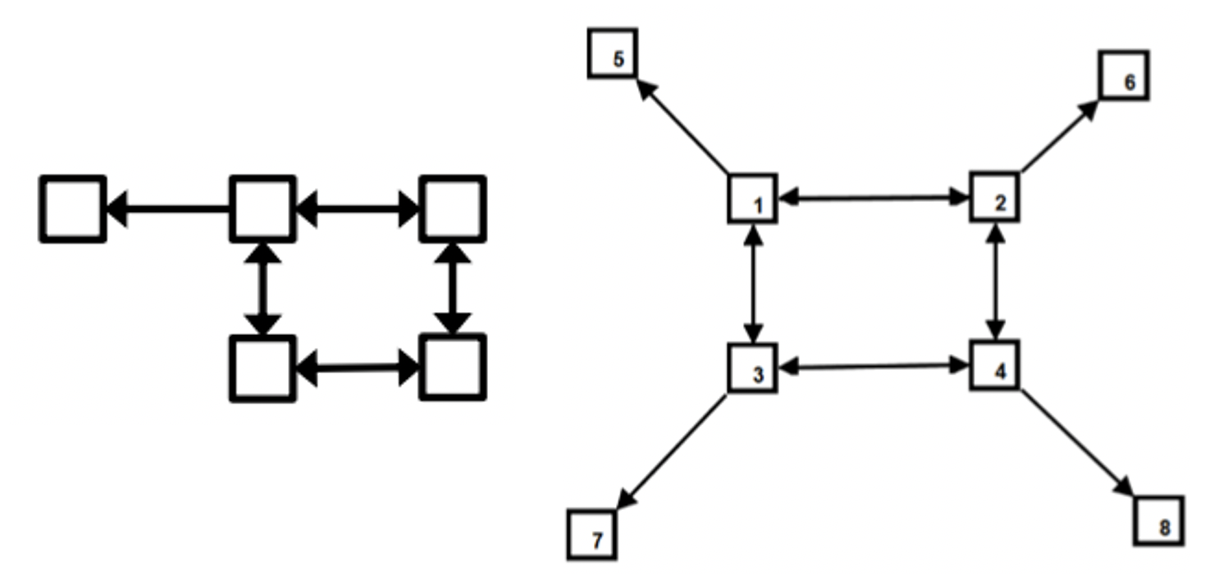
위의 그림에서 좌측은 Motif, 우측은 그래프입니다. 해당 그래프 내에서 Motif가 4번 등장하는 것을 볼 수 있으며, 이처럼 한번만 등장하는 것이 아니라 다수의 횟수로 나타나여 Motif의 자격을 얻을 수 있습니다.

Significance: More Frequent than Expected

말 그래도 예상보다 많이 등장해야 하며, “예상보다”라는 뜻은, Random Graph에서 등장하는 빈도보다 많아야 한다는 뜻입니다.

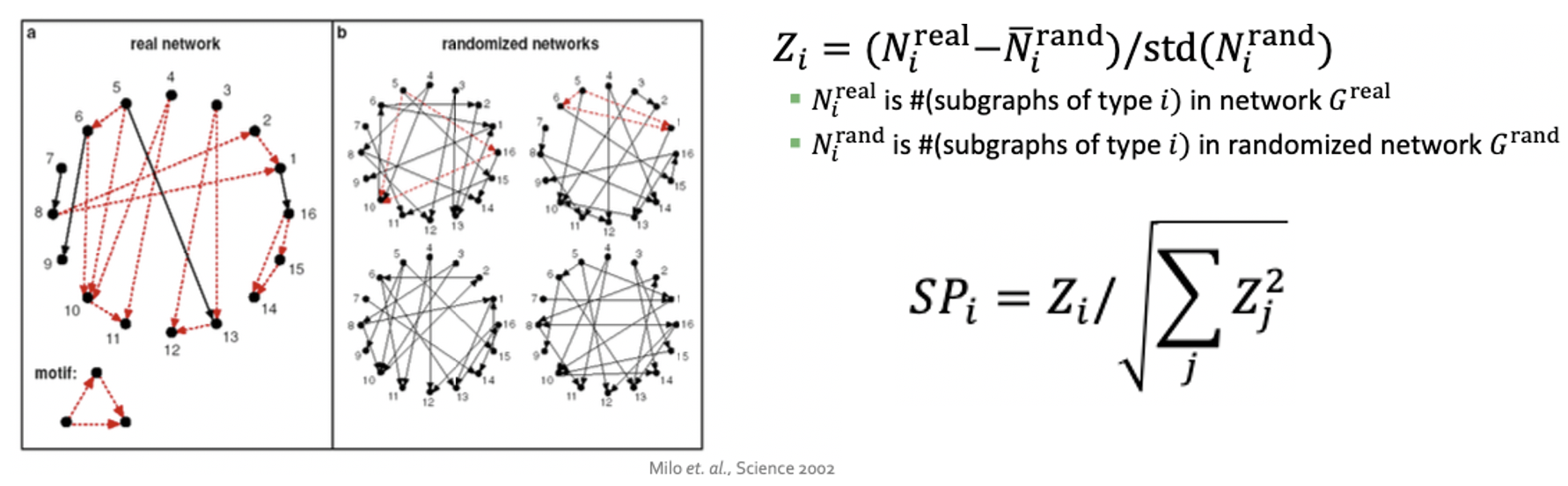
좌측의 Real Network에서 빨간색으로 표시된 Subgraph가 Motif이며, 이는 우측의 Random으로 생성한 그래프보다 더 많이 등장하기에 해당 그래프를 특징지을 수 있는 Motif입니다. 해당 Significance를 나타내는 $Z_i$는 Random Graph에서 나타나는 Motif의 평균을 빼고 분산으로 나누는 꼴을 갖는데, 따라서 평균이 작고 분산이 작을수록 Motif Significance가 증가하는 것입니다. 그리고 평균과 분산이라는 말이 등장한다는 뜻은 Random Graph를 여러 번 생성한다는 것을 나타내기도 합니다.

학생의 질문

Q: 왜 굳이 Random Graph랑 비교하나요? 그냥 빈도가 높으면 그것으로 Motif가 중요하다고 생각하면 되지 않나요?

A: 물론 그럴수도 있지만, Graph의 Size / Density가 커지게 된다면 자체적으로 빈도가 많을 수 있기 때문에 상대적인 비교가 필요하다스키.

그럼 이어서 질문이 생길 수도 있습니다. Random Graph는 어떻게 생성할까요? 이전 챕터에서 배운 Random Graph 모델을 그래도 사용하나 싶었지만 해당 모델들은 지나치게 간단하여 Real Graph와 너무 동떨어진 Graph라고 합니다. 따라서 Random도 ‘제대로’ 설정하기 위하여 Null Model을 사용하며 이것이 Configuration Model이라고 합니다.

Null Model: 이름이 Null Hypothesis과 유사한데 기능도 유사하여, Real Network의 Motif가 우연히 발생한것이 아니라는 것을 검증하기 위해 사용되는 Random Model입니다.
Configuration Model: Random Graph를 구성할 때, 각 노드의 Degree를 최대한 유지하려는 모델입니다.
Switching: Configuration Model을 구성할 때 Default Configuration Model과 조금 다르게 Endpoint를 교환하는 방법

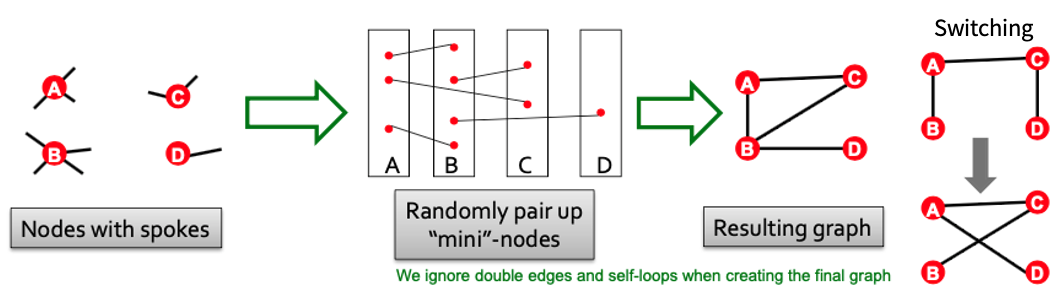
Configuration Model을 통해 Subgraph Significance를 계산할 수 있게 됩니다. 그리고 Significance가 높은 Subgraph를 Motif라고 규정지을 수 있습니다. 위에서 Motif의 정의를 설명드렸으나 사실 가장 Default의 정의이며 다양한 Variation이 있기에 필요에 따라서 정의가 약간 바뀔 수도 있습니다.

Graphlets

다음으론 Graphlets에 대하여 살펴보겠습니다. Motif의 효용성에 대해서 다시 생각해보면 Network Motif를 통해 전체 Graph를 특징지을 수 있다는 것이었습니다. 물론 Graphlet도 Graph를 특정짓는 구성 원소로서의 역할을 하긴 하지만, 좀 더 세분화 된 개념입니다.

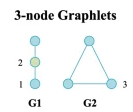
위는 노드가 3개가 있는 Graphlet의 종류입니다. Motif의 관점으로 살펴보면 G1 / G2로서 두 가지 Motif가 존재한다고 할 수 있지만, Graphlet의 관점에서는 3-node graphlets에는 3가지 Graphlet이 존재하며, 이는 노드의 위치로서 구분할 수 있습니다. G1를 살펴보면 1,2 Node가 존재하는데 G1을 아래와 같이 두 경우로 분류할 수 있습니다.

구심점(Orbit)이 1번 노드: 가외에 있는 노드가 중심이다.
구심점(Orbit)이 2번 노드: 중앙에 있는 노드가 중심이다.

G2같은 경우에는 3번 노드밖에 존재하지 않는데 그 이유는 3번 노드가 어디에 있어도 똑같은 Graphlet이기 때문입니다.

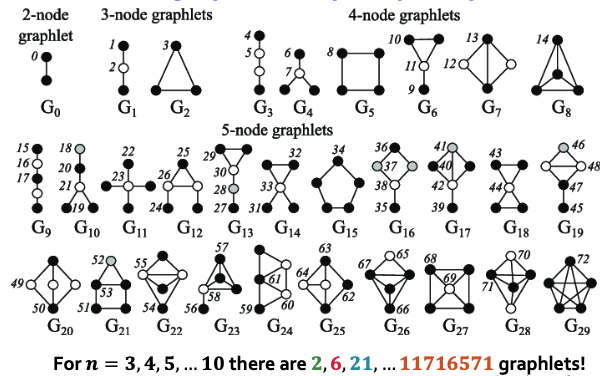
따라서 다음과 같이 노드 개수별 Graphlet을 정의할 수 있고 5개 노드까지는 72개의 Graphlet이 존재한다고 할 수 있습니다. 그럼 이 Graphlet으로 무엇을 할 수 있을까요? Motif보다 좀 더 세분화된 개념으로 Graphlet Degree Vector를 생성하여 Graph를 특징지을 수 있습니다.

이 때 Degree라는 개념이 이름에 포함되어 있는데, 원래 Degree의 정의는

하나의 노드와 연결되어 있는 Edge개수

입니다. 하지만 이 개념을 Graphlet의 관점에서 일반화 시켜본다면, Graphlet Degree란 하나의 노드가 구성할 수 있는 Graphlet을 나타냅니다. 아래의 예시를 통해 부연 설명해보겠습니다.

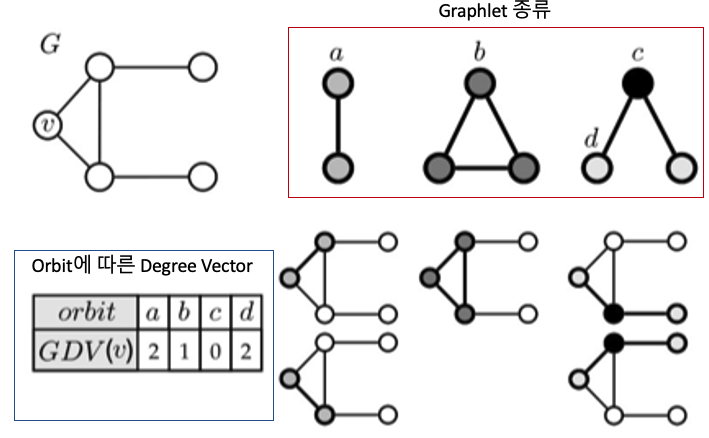
$v$ 노드에 대한 GDV를 정의하기 위해선 $v$노드가 구성할 수 있는 Graphlet을 기록해야합니다.

빨간 박스: Node 개수에 따른 Graphlet 종류
파란 박스: Orbit에 따른 Degree Vector

$v$ 노드의 관점에서 a orbit graphlet은 2개, b orbit graphlet은 1개, 그리고 d orbit graphlet은 2개입니다. 강의를 들으면서 의아했던 부분은 왜 c부분의 graphlet이 하나도 없냐는 부분이었습니다. 왜냐면 $v$ 입장에서 삼각대 형태가 구성되는게 명확하기 때문입니다. 하지만 Motif와 마찬가지로 Graphlet도 Subgraph이기 때문에 구성의 단계를 “Node $\rightarrow$ Edge”로 생각해본다면, 노드 C를 Orbit으로 구성하기 위해선 아래 두 노드를 포함해야 하는데 그럴 경우, 아래 두 노드끼리 연결이 되어버리기 때문에 b orbit graphlet이 형성되기에 불가능합니다. 이 부분이 조금 이해가 어려울 수 있으나 곱씹어보시면 도달하실 수 있으실 겁니다.

Structural Roles in Networks

Role이란 역할로서, Network내에 노드들이 갖는 “Function”이라고 정의됩니다.

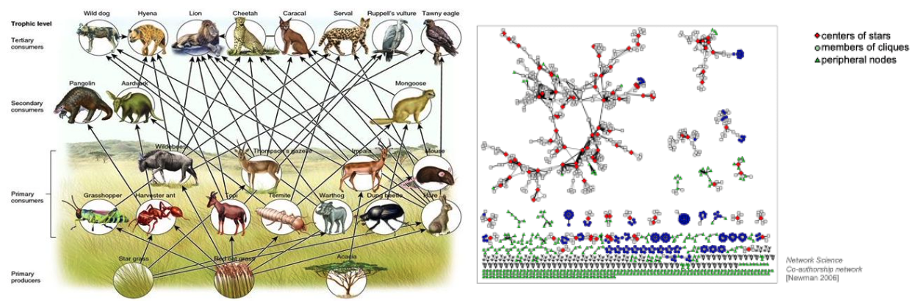
예룰 들어 다음과 같이 “Food Chain”의 Graph가 존재한다면, 맨 아래의 식물들은 Primary Producers라는 역할을 갖고, 사자는 “포식자”라는 역할을 갖게 되는 것입니다. 이런 역할들은 Structural behavior로 측정이 되며,

Centers of start
Members of Cliques
Peripheral Nodes

등과 같이 전체 그래프 구조에서 차지하는 위치나 행동으로 나타낼 수 있습니다. 따라서 Role의 특징을 좀 더 정리해보자면,

같은 Role을 갖는 node들은 연결된 노드들이 비슷하다.
같은 Role을 가졌다고 가까운 장소에 있는 것이 아니라, 비슷한 장소에 존재한다.

그리고 여기서 Role과 Community라는 개념의 비교를 하게 되는데, Community란 잘 연결된 노드들의 집합을 의미합니다. 강의에서는 딱히 확실한 정의를 내리지는 않지만 Computer Science Department의 예시를 살펴보게 된다면,

Roles: Faculty, Staff, Students
Communities: AI Lab, Info Lab, Theory Lab

와 같은 꼴을 갖게 됩니다. 즉, 다양한 종류에 Community에 여러가지 공통의 Roles들이 자리잡게 되는 것입니다.

Roles: More Formally

Role을 더 공식적으로 정의하자면, Structural Equivance를 갖는 노드들의 집합이라고 정의할 수 있습니다.

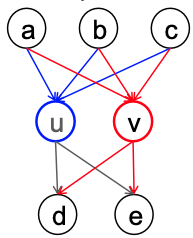
위의 그림과 같이 $u, v$는 같은 Role을 가지며, 구조적으로 동일하다고 할 수 있는데, 위아래로 연결된 노드의 개수가 동일하고 연결된 방식도 동일하기 때문입니다. 그럼 하나의 그래프 내의 Role을 자동적으로 탐지하고 분석해내는 기법은 어떤 것이 있을까요?

Discovering Structural Roles in Networks

먼저 Role을 찾아내는 것이 왜 중요한가에 대한 답은 [Node의 특성을 파악하기에 용이]하기 때문입니다. 이를 가능하게 하는 기법 중에는 대표적으로 ‘RolX’가 있으며 롤렉스라고 읽습니다.

RolX

Unsupervised Learning Approach이기에 Prior Knowledge가 필요 없다.
각 노드에 대하여 Mixed Membership of roles를 부여하여, Mixture Model과 유사한 방식을 택한다.

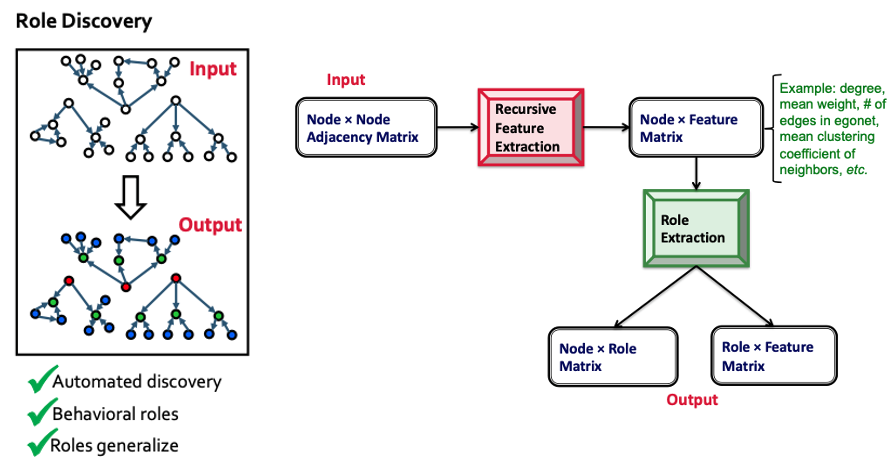
RolX를 통해 위의 좌측의 그림처럼 Graph를 Input으로 넣었을 때, 자동적으로 각 노드의 Role을 Return해줄 것입니다. 이를 위하여 우측의 방식을 거치게 되는데

(Node x Node) Adjacency Matrix를 Input으로 넣는다.
Recursive Feature Extraction을 적용한다.
RFE를 통해 각 Node의 Feature를 Return한다.
Role Extraction을 통해 두 Matrix를 Return한다.
- (Node x Role) Matrix: 각 노드가 어떤 Role을 가졌는가?
- (Role x Feature) Matrix: 각 Role은 어떤 Feature를 갖는가?

Recursive Feature Extration

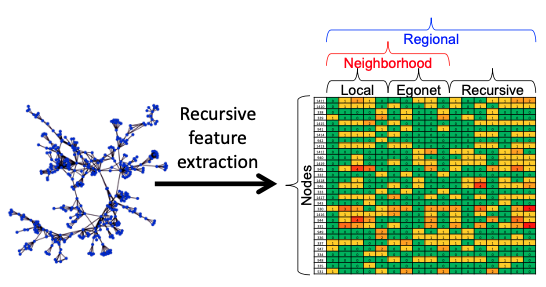
해당 개념은 실제 논문을 읽어봐야 할 정도로 강의자 분께서 생략을 한 부분이 있는 것 같습니다. 따라서 제가 이해한 부분만 정리하고 넘어가도록 하겠습니다.

하나의 Graph를 Input으로 사용하였을 때, 구조적인 정보만으로 Node의 Feature인 Role을 파악하려고 하는 것이므로, Adjacency Matrix를 사용합니다. 이를 통해 RFE를 사용하게 된다면 위의 우측 Matrix와 같은 꼴이 나타나며, Matrix의 앞 부분은 Neighborhood feature를 담은 Local / Egonet Feature를 담으며 뒷부분은 Recursive Feature를 담습니다.

Local Feature: 하나의 노드의 지협적인 구조 특징을 담는다 (e.g Degree)
Egonet: 특정 노드를 중심으로 펼쳐지는 Subgraph라고 생각하면 된다.
Recursive: 나머지 부분을 Recursive하게 계산한다고 하는데 이 부분을 잘 모르겠습니다.

RolX 기법을 통해 Feature들이 정리되면 Clustering 기법으로 각 노드들에게 Role을 부여합니다. Clustering기법은 사실 현존하는 모든 기법을 사용해도 되나, RolX는 아래의 기법들을 사용했다고 합니다.

Clustering $\Rightarrow$ non-negative matrix factorization
Model Selection $\Rightarrow$ MDL
Measure Likelihood $\Rightarrow$ KL Divergence

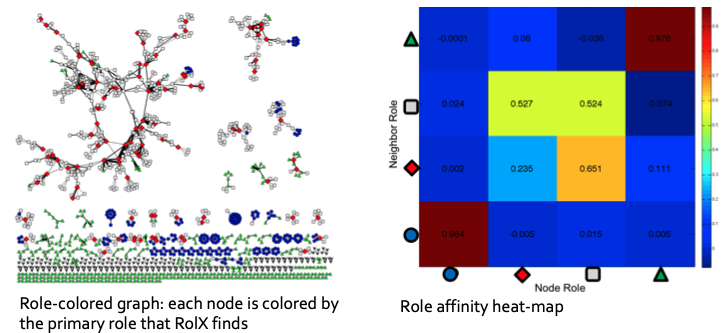
결과적으로 다음과 같은 Role-Colored Graph와 Affinity Heat-map이 나타나게 됩니다. 여기서 살펴볼만한 것은, 반드시 대각원소만이 높은 값을 갖고 있지 않다는 뜻입니다. 즉, 같은 Role을 가진 노드끼리의 인접성만 높은 것이 아니라, 비슷한 Role을 가진 노드들 간의 인접성도 꽤 높다는 것입니다.