CS224W Lecture 1

Posted on |
Machine Learning with Graphs

CS224W 1번째 강의 정리를 정리해보았습니다. 강의에서 사용된 이미지 전체는 CS224W 수업 자료에서 가져왔음을 미리 밝히는 바입니다.

“Network란 상호작용하는 Entity를 표현하는 복잡한 System이다”

정의

일반적으로 Network와 Graph는 혼용됩니다. 하지만 둘의 개념은 차이가 있으며, Network 쪽이 좀 더 상위의 개념이라고 생각이듭니다.

Networks (also known as Natural Graphs)

  • Society는 70억 명의 개인의 집합이다.
  • Communication Systems는 전자 기기들을 연결한다.
  • Gene / Protein들의 상호작용

들과 같이 자연 현상에서 나타나는 객체들간의 관계를 Network라고 표현합니다. 이는 다소 추상적인 개념이므로, 이에 대한 계산과 분석을 위해선 구체화를 시켜야 하는데, 이것을 Graph라고 하는 것입니다.

Graphs (Information Graphs)

  • Information / Knowledge Graph
  • Scene Graphs: 하나의 Scene 안에 있는 객체들이 어떻게 관계지어지는 지
  • Similarity Networks: Data 사이의 유사한 데이터 객체를 잇는 그래프

추상적인 네트워크를 구체적, 수학적으로 나타내면 그래프가 됩니다. 따라서 실제 Task와 밀접해있는 구조라고 생각하시면 됩니다. 두 개념은 위에서 말했듯이 혼용되며, 실제 강의에서도 여러 번 바뀌어 사용이 됩니다. 두 개념을 다르기에 구성 개념 역시 같은 역할을 해도 다른 이름으로 부릅니다.

Network Graph
Node Vertex
Link Edge

Networks: Knowledge Discovery

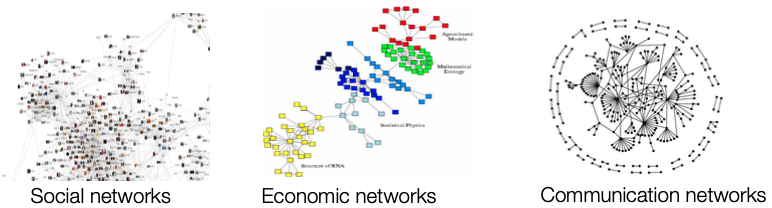
image-20210105213819855

세상에는 다양한 시스템이 존재합니다. 사회, 통신, 경제 시스템과 더불어 인터넷도 하나의 시스템입니다. 하지만 시스템은 매우 복잡하여 온전히 이해하기 힘든데, 시스템 속의 네트워크를 파악해야 가능해지는 부분입니다. 시스템 구성 객체간의 상호작용을 파악하기 위해선 네트워크를 분석해야 합니다. 이런 네트워크를 수리적으로 표현한 것이 Graph라고 할 수 있으며, Graph에서 나타나는 ‘관계’들을 modeling 함으로써 시스템 파악을 할 수 있는 것입니다.

Network 분석법

  • 그래프 내의 주어진 노드의 타입을 분류하는 것: Node Classification

  • 노드가 연결되어 있는 지, 또는 연결 될지 예측하는 것: Link Prediction

    특정 사람 또는 카테고리와 상품이 연결이 될지 안 될지를 판단하는 Link Prediction 을 통해 Content Recommendation이 가능합니다.

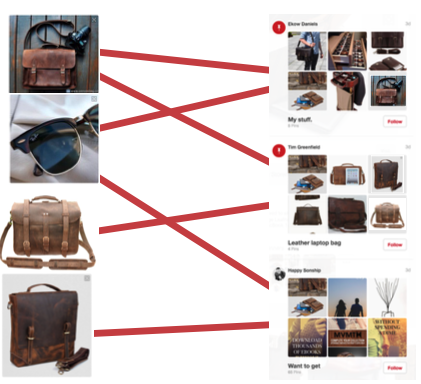
    image-20210105213940724

  • 밀접해있는 Node Cluster를 찾는 것: Node Clustering / Community Detection

  • 두 노드나 네트워크끼리의 상호 유사성을 측정: Network Similarity

Networks의 구조

위에서 그래프는 시스템에 존재하는 네트워크를 표현하는 표상이라고 말씀드렸습니다. 표상은 표현하고자 하는 대상을 얼마나 잘 묘사 또는 반영했느냐에 따라 좋은 표상이 됩니다. 따라서 Network Representation인 그래프를 잘 선택해야 하며, 강의에서 다양한 그래프에 대한 소개를 진행합니다.

Undirected / Directed

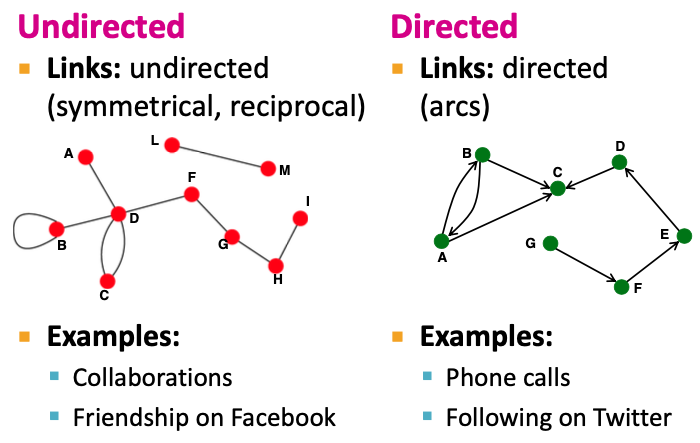
image-20210105214602445

Undirected Graph는 Edge의 방향성이 없는 그래프입니다. 따라서 연결이 되었다면 두 Vertex가 서로에게 영향을 주는 것입니다. 따라서 관계가 대칭적 / 상호적입니다. 강의에서는 ‘협업’을 Undirected의 예시로 설명했는데 그 이유는, (정상적인) 협업관계에서는 한 쪽만이 다른 한 쪽을 도와주는 것이 아닌 서로를 조력하는 것이기 때문에 Edge의 방향이 서로에게 향하기 때문입니다.

Directed Graph는 Edge의 방향이 존재합니다. 이는 한 Vertex가 다른 Vertex를 향해 Edge가 뻗어 있더라도 돌아오는 화살표는 없을 수도 있다는 뜻입니다. 예를 들어, 전화 통화 같은 경우에, 한 쪽이 일방적으로 전화를 거는 경우만 있고 콜백이 없을 수도 있는 관계라고 할 수 있습니다.

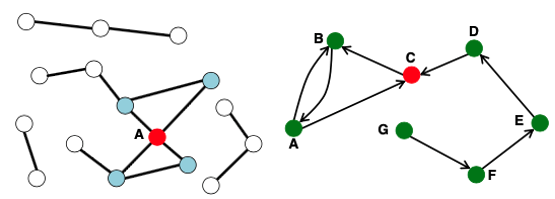
image-20210105215050272

Node Degree (Undirected / Directed)에 따른 그래프 분류

  • Undirected

    Node Degree: 하나의 노드에 연결된 Edge의 개수

    Avg. Degree: $\bar k = \frac{1}{N}\sum_{i=1}^{N}k_i = \frac {2E}{N}$

  • Directed

    방향성 그래프는 노드의 Edge가 방향이 존재하기 때문에, 해당 노드로 향하는 Edge (In-degree) / 해당 노드에서 나가는 Edge (Out-degree)를 구분해서 표기해야 합니다.

    Avg.Degree: $\bar k = \frac {E} {N}$

    위의 Undirected는 하나의 Edge가 두 노드가 모두 상호 연결되어 있기 때문에 Edge가 각 노드마다 있다고 생각하여 2를 곱해주지만 Directed에서는 단순히 Edge의 개수를 모두 더하고 전체 Node로 나눈 값이 평균 Degree가 됩니다.

Special Case of Graph

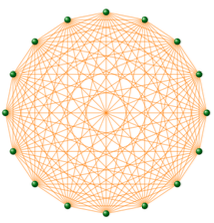
  • Complete Graph

    Undirected Graph 내에서 노드들끼리 완벽하게 연결되어 있는 그래프를 Complete Graph라고 합니다. 따라서 Edge의 수가 그래프가 가질 수 있는 Edge의 최대값을 가지게 되며 이는 다음의 수식과 같습니다.

    $E_{max} = \frac {N(N-1)}{2}$ image-20210105215909084

  • Bipartite Graph

    Bipartite Graph는 그래프 내에서 U / V의 Set로 분리될 수 있는 node들을 갖고 있는 그래프를 말합니다.

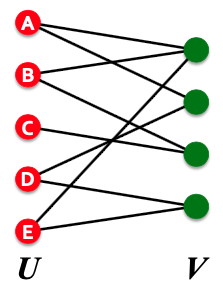
    image-20210105220355065

    위의 그림과 같이 U set과 V set은 set 내의 연결은 없지만, set 간의 연결은 존재합니다. 이는 $k$-partite graph의 특수한 경우이며, U와 V set 내의 각 원소들은 Independent합니다. Bipartite Graph를 구성할 수 있다면 다음에 소개해드릴 Folded / Projected Biparted Graph를 구성할 수 있습니다.

  • Folded /Projected Bipartite Graph

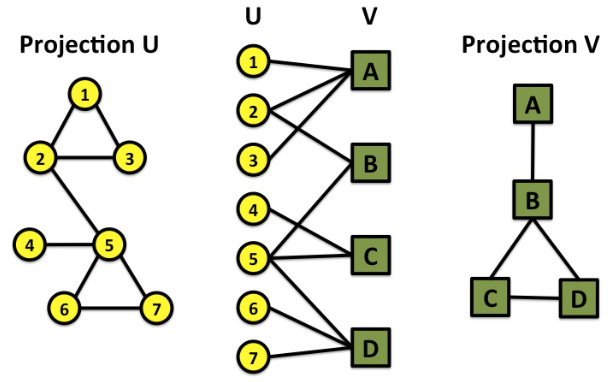
    image-20210105220837469

    중간에 있는 Bipartite Graph로부터 도출해낼 수 있는 그래프입니다. Folded Graph가 표현하고자 하는 바는 ‘같은 Root가 존재하면 연결한다’ 라는 의미입니다. 우측의 Projected Graph를 살펴봤을 때, A / B Vertex는 U set의 [2]번 Vertex를 같은 뿌리로 삼고 있습니다. 따라서 두 Vertex가 연결이 되게 되며, A와 C Vertex는 같은 U vertex 뿌리를 갖고 있지 않기에 연결이 되어 있지 않습니다.

Adjacency Matrix

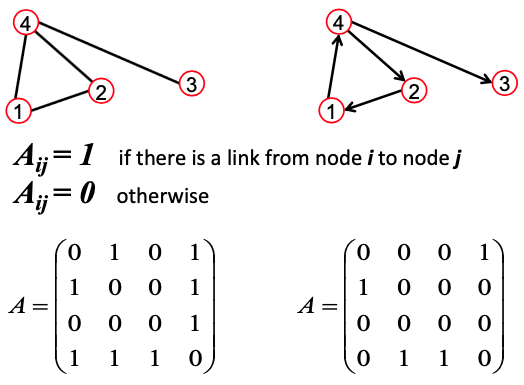
image-20210105221205747

Adjacency Matrix는 번역하면 ‘인접행렬’입니다. 말 그래도 어떤 Vertex가 Edge로 연결이 되어 있는지 0/1로 표기하는 것입니다. 이 때, Undirected Graph는 Symmetric Adjacency Matrix를 가지며, Directed Graph는 Symmetric하지 않습니다.

Connectivity

Adjacency Matrix만 살펴봐도 바로 판단할 수 있는 그래프의 특징 중 하나는 Connectivity 입니다.

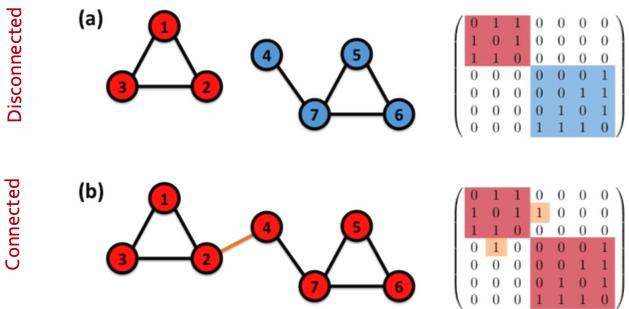
image-20210105222826701

이는 위의 그림이 매우 명확하게 표현하고 있는데, Disconnected Graph인 경우에는, Block Diagonal Form을 가지며 대각선 위치에 사각형 모양으로 연결이 형성됩니다. 반대로 Connection이 존재하는 경우에는 Diagonal 이외의 위치에 1이 존재하는 것을 볼 수 있습니다. 해당 특징을 좀 더 발전시킨 것이 나중에 배우게 될 Spectral Clustering 입니다.

Network는 매우 Sparse하다!

image-20210105221545673

Network는 Sparse하다는 것을 느끼기 위해선 좌측의 Adjacency matrix를 살펴보면 됩니다. 색칠되어 있는 것이 연결 상태라고 했을 때, 빈 공란이 많이 있다는 것을 알 수 있을 것입니다. 우측의 표를 살펴본다면, Benchmark Dataset들이 갖고 있는 Node들이 최소 천개, 많게는 억대를 상회하는데 평균 Degree는 10대 안팎입니다. 이는 확실히 그래프의 노드 개수에 비해 연결 빈도가 낮다는 뜻이며 Sparse 하다는 결론에 도달하게 됩니다.

더 다양한 그래프 꼴

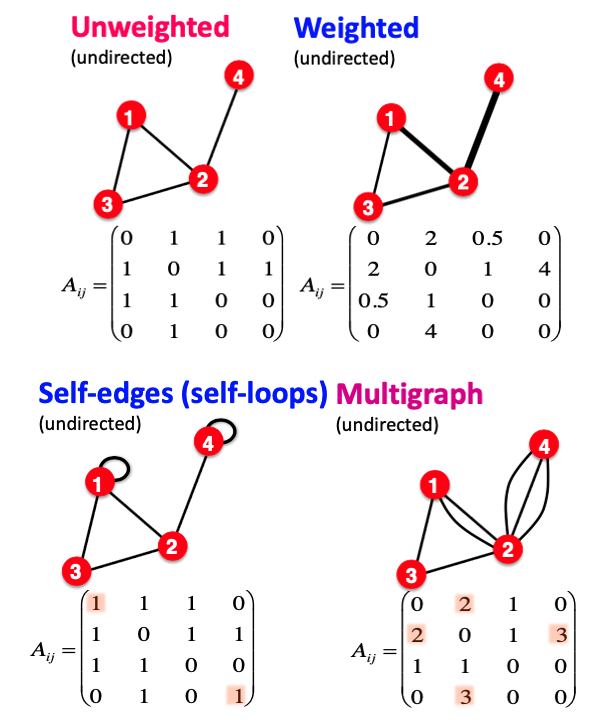
image-20210105222524501

  • Edge Weight가 존재하는가? (Unweighted / Weighted)
  • 자신을 가리키는 Edge가 존재하는가? (Self-edges)
  • 하나의 노드에 포함된 Edge가 하나 이상인가? (Multigraph)