PageRank
Abstraction
웹페이지에 대한 선호도는 확실히 주관적이며, 개인의 취미 또는 선호도에 따라 천차만별입니다. 따라서, World Wide Web 내에 존재하는 모든 사이트들에 대하여 일정한 순위를 매기기는 어렵습니다. 하지만 네이버가 hoonst.github.io보다는 선호하는 사람이 많고 WWW내에서 차지하는 비중이 훨씬 높을 것입니다.
Pagerank는 웹”페이지” 내에 잠재되어 있는 Rank를 파악하려 하는 알고리즘이며, 구글의 창립자 래리 페이지의 연구 프로젝트의 일환으로써 개발된 것입니다. 친구이자 같은 대학원생이었던 세르게이 브린이 함께 참여했으며, 해당 PageRank 알고리즘의 검증을 위하여 Google이라는 Web Search Engine을 만들었다고 합니다 (논문 2페이지).
To thest the utility of PageRank for search, we built a web search engine called Google
PageRank를 통해 “중요한 웹사이트”를 판단하는 기준은,
- 얼마나 많은 사이트들이 참조했는가?
- 참조한 사이트들의 영향력은 얼마나 큰가?
입니다. 즉, 뒤에서 자신을 참조한 대상을 계산에 사용하기 때문에 원래 프로젝트 이름은 BackRub이었다고 하며, 나중에 Google로 변경했다고 합니다.
1. Introduction & Motivation
일반 문서들과는 다르게 웹 문서들은 서로를 참조하는 링크를 걸 수 있으며, 이에 따라 링크와 노드로 이루어진 그래프 구조를 가질 수 있습니다. 그리고 그 그래프를 사용하여 어떤 노드가 중요도가 높은지를 판단하여, “중요한 웹페이지”를 탐색해나갈 수 있습니다.
PageRank이전에도 문서들의 관계에 대하여 탐색한 여러 시도들이 있었는데, 웹 문서들 보다는 확실히 Citation을 통해 Link Structure를 쉽게 구성할 수 있는 논문들을 대상으로 많이 진행이 되었습니다. 즉, PageRank의 대상인 Web Page와 Academic Paper의 속성이 많이 다르다는 뜻입니다.
학술 논문과 웹페이지의 특징
- 학술 논문 - 꼼꼼히 점검되었고, 논문끼리 형태 및 Citation의 갯수가 유사하다.
- 웹페이지:
- 제한 없이 생성되고 증식한다.
- 웹페이지는 방문자 수에 따라 수익이 결정되기 때문에, 이목을 끌고자 하는 전략들이 존재하고 이로 인해 순위 조작의 위험에 노출되어 있다.
- 페이지들의 유사성이 학술 논문보다는 적고, Link도 다양하다.
- 웹페이지의 경험적 퀄리티는 높은데 그 이유는 애초에 퀄리티가 낮은 웹페이지는 잘 안 읽고, 어느정도 퀄리티가 보장되어야 읽기 때문이다.
2. A Ranking for Every Page on the Web
위에서 Pagerank이전에는 학술 논문의 Citation을 통해 문서들의 관계를 살펴보고자 하는 시도들이 많았다고 했습니다. 해당 연구들에서는 많이 인용이 된 논문은 중요한 논문이라는 가정을 갖고 있습니다. 예를 들어, Transformer를 소개한 논문 “Attention Is All You Need”는 현재 인용이 14714회인데, 단순히 숫자만으로도 해당 논문의 영향력을 알 수가 있습니다. 이렇게 인용 수로만으로도 논문의 중요성을 판단할 수 있는 이유는, 모든 학술 논문들이 양질의 글이며, 허투루 쓰여진 글이 아니기 때문입니다.
하지만 웹에서는 모든 웹페이지가 양질이 아닐 수 있습니다. 악명 높은 네이버 블로그의 무정보성 포스트부터 다양한 광고성 글 등 중요하지 않은 글들이 존재하는 반면, Jay Alammar의 블로그나 ratsgo 블로그처럼 중요한 글들이 존재합니다.

즉 페이지마다의 중요도가 다르고, 어떤 페이지로부터 Link가 연결되어 있는지가 중요합니다. 만약 위에서 언급한 블로그 중에 어느날 갑자기 제 블로그에 링크를 걸었다면 그 영향력이 매우 클 것이지만, 저와 전혀 상관없는 알려지지 않은 사람이 저의 블로그에 링크를 거는 것은 의미가 없을 것입니다. 이렇게 연결의 양뿐만이 아니라 연결 주체 및 대상에 대한 고려를 하는 것이 PageRank입니다.
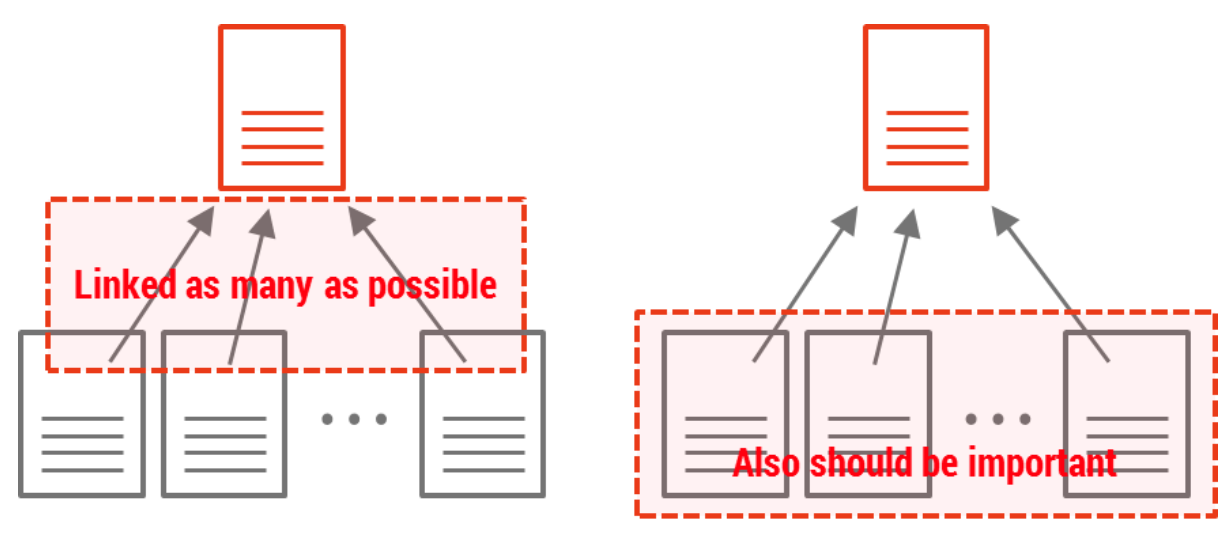
링크의 양만을 고려하는 것이 아니라 연결 주체를 고려하게 되면 다음과 같은 상황을 산정할 수 있습니다.
- 경우 1: 100개의 광고성 포스트가 내 블로그에 링크를 걸었을 때
- 경우 2: Ratsgo 블로그에서 내 블로그에 링크를 걸었을 때
이 경우, 경우 1보다 경우 2의 링크의 갯수는 현저히 적지만, 그 의미는 저에게 있어 엄청 클 것인것은 물론, 객관적인 PageRank도 매우 커질 것입니다.
A page has high rank if the sum of the ranks of its backlinks is high.
Link Structure of the Web
본 논문 작성시에 크롤링할 수 있었던 Web은 150 million page (node)와 1.7 billion links (edge)로 구성되어 있습니다. 모든 페이지는 두 종류의 Link를 갖고 있습니다.
- Forward Link(Outedges) - Link가 가리키는 곳
- Backward Link(Inedges) - Link의 발원지
크롤링을 진행하여 하나의 페이지를 살펴보면, 어떤 페이지가 해당 페이지를 참조했는 지는 모릅니다. 지금 이 순간에도 제 블로그를 참조하는 사이트가 있을지도 모르지만, 전혀 모르는 것과 같습니다 (아마 없겠죠…). 하지만 제가 참조하고 있는 페이지들은 바로 알 수 있습니다. 위에 있는 Jay Alammar와 Ratsgo와 같이 말입니다.
Pagerank 정의
$R(u) = c \sum\limits_{v \in B_u} \frac {R(v)} {N_v}$
해당 정의는 위에서 언급한 정의들이 식으로 반영되는 Simplified Version입니다. 식에 포함된 Notation을 살펴보겠습니다.
- $u$: Web Page
- $F_u$: Forward Link (Link가 향하는 곳)
- $B_u$: Backward Link(Link 발원지)
-
$N_u$: $u$로부터 발산하는 Link 갯수 = $ F_u $
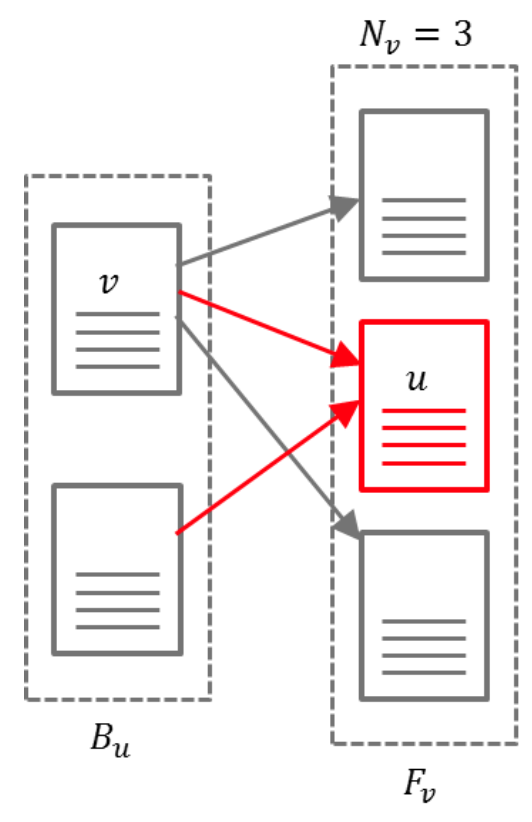
위의 식을 풀어서 써보자면,
“한 웹페이지의 PageRank($R(u)$)는 해당 페이지를 참조하는 모든 $B_u$ 들에 대하여, $B_u$의 PageRank를 발산하는 Edge 갯수로 나눈다” 라고 할 수 있습니다. $c$는 Normalizing Constant입니다.
논문에는 나와있지 않지만, $N_v$가 ‘웹 페이지’의 특성을 반영한 계산 요소라고 생각이 듭니다. 만약에 정말 Rank가 높고, 높을만 한 사이트들 (Naver / Kakao) 라면 다른 사이트들을 신중하게 참조할 것이며, 이미 자신들이 거물이니 딱히 다른 사이트들을 참조할 필요성이 크게 없습니다. 따라서 $N_v$는 애초에 작을 것입니다. 하지만 광고성 페이지나 수익 창출만을 목적으로 하는 사이트라면 최대한 많은, 연관이 있든 없든 많은 사이트들을 참조를 걸 것입니다. 따라서 해당 페이지들에 대한 Rank가 다른 페이지로 흘러가는 비율을 줄이는 역할을 하여 정화 작용을 하지 않나 싶습니다.
여기까지의 PageRank 개념은 매우 쉽게 다가올 수 있습니다. 하지만 PageRank는 은근히 포함되어 있는 개념들이 많아 이를 반영한 설명도 함께 설명하고자 합니다.
Pagerank Matrix Form
$A$라는 정방행렬의 row와 column을 각 웹페이지 $u,v$라고 설정해보겠습니다. 그리고 $A_{u,v}$는 $u$에서 $v$로 링크가 향해있다면 $1/N_u$로 값을 넣습니다. $N_u$는 링크의 갯수이기 때문에, $u$의 PageRank가 Iteration을 통해 변한다 하더라도 갯수는 변하지 않습니다.
그리고 $R$ 벡터에 전체 노드의 PageRank를 넣습니다. 이를 통해 $R = cAR$의 꼴을 만들어 PageRank가 전파되는 모습을 그릴 수 있고, 이 때, 맨 처음에는 $\lambda R = cAR$의 꼴이겠지만, $\lambda$를 1로 만들면 좌항, 우항이 같게 됩니다. 따라서 $\lambda$, 즉 Eigenvalue가 1인 Eigenvector가 Iteration을 통해 수렴한 Pagerank가 되는 것입니다.
Pagerank Exception
위의 Simplified Version이 모든 경우에 적용이 되면 좋겠지만, 아쉽게도 그렇지 않은 예외의 경우가 있습니다.
- (Spider Trap): Node들이 자기들끼리만 Linked 되어 있는 경우
- (Dead End / Dangling Node): Node가 연결이 되어 있지만, 해당 Dangling Node는 다른 노드로 연결이 향하지 않는 경우
위의 문제를 해결하기 위하여, Rank Source를 설정합니다.
Rank Source에 대한 정의는 놀랍게도 논문에서 나타나지 않습니다. 하지만 여러 자료를 살펴보고, 특히 지식의 정석, wikipedia를 살펴보고 다음과 같이 정의할 수 있을 것 같습니다. 그리고 왜 이걸 제대로 정의를 안해놨는지에 대한 의문이 큽니다.
Rank Source: Some vector over the Web Pages that corresponds to a source of rank ($E(u)$)
Rank Source: Rank의 근원, 즉 Node들의 발생 확률이라고 할 수 있으며, 이는 1/(Node 갯수)라 할 수 있습니다. 본 논문에 따르면, 단순히 1로 나타내는데 Wikipedia가 이것은 잘못이라고 추측한다고 합니다.
해당 Rank Source를 반영한 새로운 Pagerank 식은 다음과 같습니다.
$R’(u) = c \sum \limits_{v \in B_u} \frac {R’(v)} {N_v} + cE(u)$
이렇게 식을 구성함으로써 $R’(u)$는 0이 되는 경우가 없어질 것입니다. Default값이 $cE(u)$가 될 것이니 말입니다. 마치 Smoothing을 하는 원리와 비슷하다고 생각합니다.
이를 Matrix Form으로 구성한다면,
$R’(u) = c \sum \limits_{v \in B_u} \frac {R’(v)} {N_v} + cE(u)$
$\Rightarrow R’ = c(AR’ + E)$ … (1)
$\Rightarrow R’ = c(A + E * 1)R’$ … (2)
가 됩니다.
위의 식에서 이상했던 부분은, $\Rightarrow R’ = c(AR’ + E)$ 의 $E$ 부분에서 $R’$이 튀어나오는 것이었습니다. 식만 보아하니, $E$안에 $R’$이 포함되어 있었고, 그것을 뺀것인가 싶었지만 논문에서는 $|R’| = 1$이기에 가능한 것이라고 합니다. 이 부분이 이해가 안가 정말 많은 시간을 사용했지만, 결국 행렬을 다룰 때는 차원에 대하여 주의를 해야한다는 교훈을 얻고 해결하게 되었습니다.
N개의 Node가 있고 그것의 Rank를 표현한 것이 $R’$라고 하면, 이는 $(N , 1)$ 차원입니다. 그리고 N개 Node 끼리의 Transition Matrix를 나타내는 $A$는 $(N, N)$이므로 $AR’$의 차원은 $(N, 1)$ 이 됩니다. 즉, $E$ 역시 $(N, 1)$ 차원이라는 뜻입니다.
$R’ = (N, 1) \Rightarrow A = (N, N) \Rightarrow E = (N, 1)$
이제 (2)번 식의 차원을 봐보겠습니다. Matrix 연산을 통해 한번에 Rank를 결정하기 위해 A와 E를 합쳐 하나의 Matrix로 만들고 싶은데 차원이 $(N, N) / (N, 1)$ 입니다. 따라서, $E$의 차원을 $(N, N)$으로 만들어야 하기에 전부 1로 구성된 $(1, N)$차원의 벡터, $1$을 추가합니다. 그리고 이로 인해 $R’$과 $E*1$의 행렬 곱이 $E$가 되어 (1)과 (2)가 동치가 되는데 그 이유는 $|R’| = 1$, 즉 Stochastic Vector이며, 1로 구성된 벡터와의 곱은 1이 되기 때문입니다.
Computing PageRank
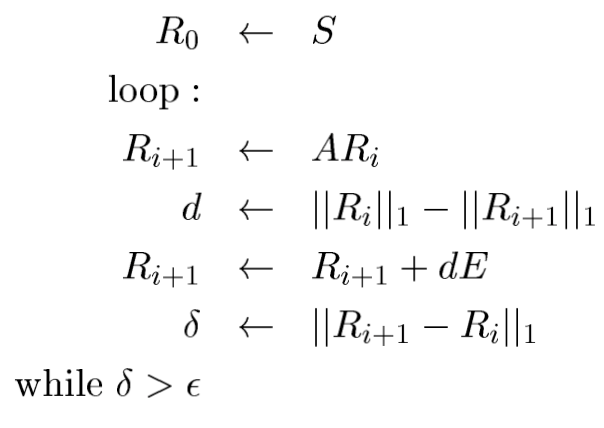
PageRank의 계산법은 다음과 같습니다.
- $R_0 \leftarrow S$ : 먼저 초기 Rank vector를 initialize해줍니다. 이 때, 단순히 1/N으로 지정하는 것이 일반적입니다.
그 후 Loop를 돌면서,
-
$R_{i+1} \leftarrow AR_i$ : Transition Matrix A와 Rank Vector를 곱해서 다음 Rank Vector를 구합니다.
-
$d \leftarrow |R_i|1 -|R{(i+1)}|_1$: 아직 해당 시기에는 Random Surfer Model의 계수를 0.8 / 0.2로 설정하는 방법을 몰랐을 때이므로, 다음과 같은 계산으로 비율을 설정한 것으로 보입니다.
- $R_{i+1} \leftarrow R_{i+1} + dE$: Random Surfer Model을 통한 E 값 합산
- $\delta \leftarrow |R_{i+1} - R_i|_1$: 새로운 Rank Vector와 기존 것의 차를 구하여, 특정 threshold를 넘으면 계속 진행, 아니면 반복을 멈춥니다. 즉, Iteration을 통하여 수렴을 하는 것을 목표로 하는 것을 볼 수 있습니다.
- $\delta > \epsilon$
Random Surfer Model
PageRank의 또다른 특징은 Random Walk입니다. Random Walk란 단순하게 표현하자면, 그래프 내에서 이동의 발자취를 뜻합니다. 따라서, 그래프 내에서 노드 A,B,C 순으로 이동했다면 $A \rightarrow B \rightarrow C$ 가 Random Walk가 되는 것입니다. Random Walk를 PageRank 안에 반영하고자 하는 이유는 ‘Random Surfer Model’을 가정하기 때문인데요. 이는 한 명의 사람이 인터넷 서핑을 할 때, Naver에서부터 네이버에 걸려있는 링크들을 타고 웹서핑을 즐길 수도 있지만, 네이버에 들어갔다가, 다음, 네이트 순으로 마구잡이로 행동할 수 있음을 반영하는 것입니다.
위에서 $E$ 같은 경우, Random Surfer가 연속적인 Link를 타고 가다 지루함을 느껴 벗어나는 경우를 표현했다고도 할 수 있습니다.
Dangling Links
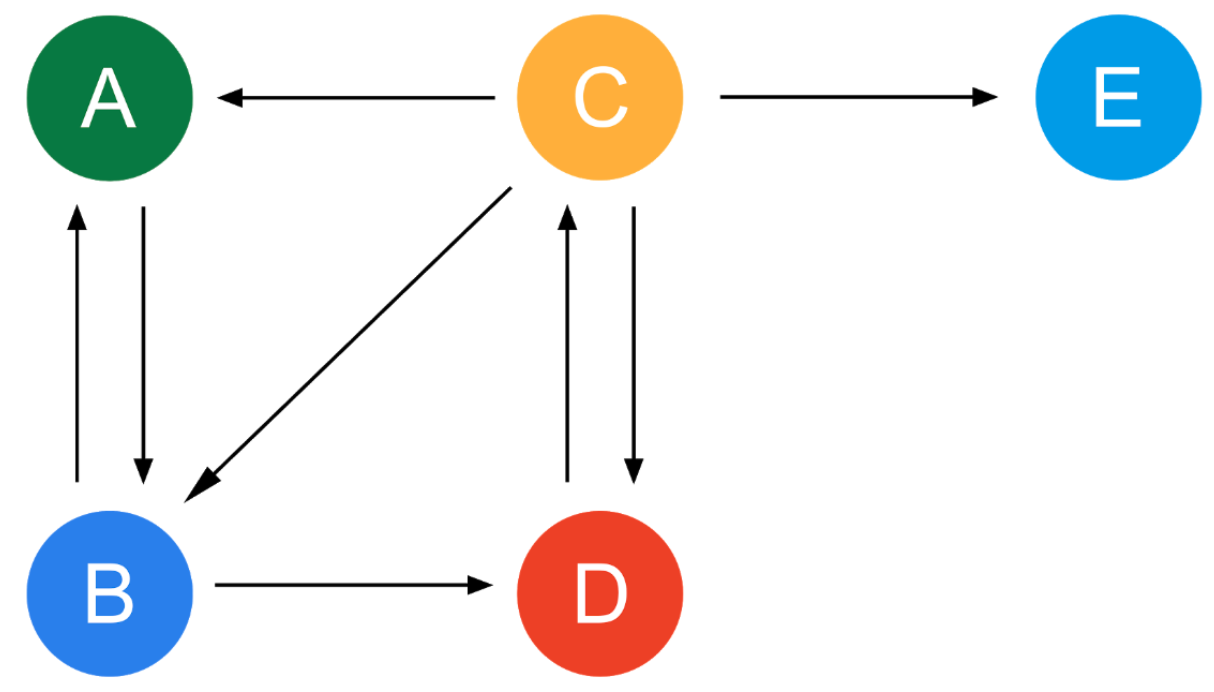
Dangling links란, 위의 그림에서 E Node 같이 Outgoing link가 없는 노드를 Dangling node라고 할 때, 이를 가리키는 링크를 말합니다. 해당 노드가 일으키는 문제로는 자신의 Rank를 분배할 다음 노드가 없다는 것입니다. 위의 그림을 그래프로 나타내면 다음과 같습니다.
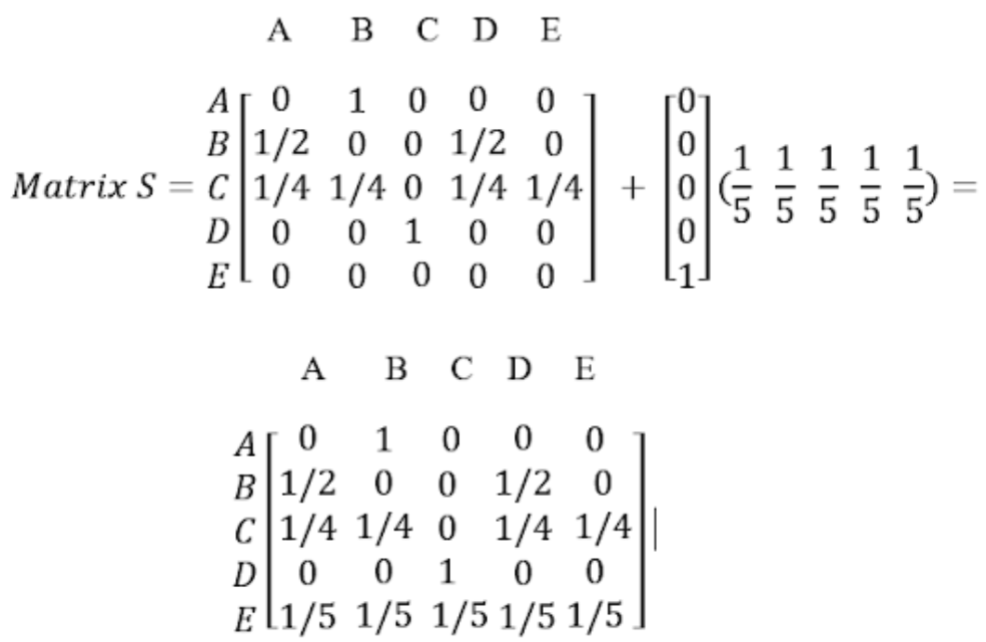
Transition Matrix가 보시다시피 Node E가 가리키는 곳이 모두 0으로 되어 있습니다. 이에 다른 행렬을 더하게 되는데 이는, E가 어디로든 연결될 수 있도록 $1/N$ 만큼 더해주는 행렬입니다.
원 논문에서는 이런 Dangling Node를 제거하고 모델을 구축하지만, 이후에 나타난 식들에서는 이를 조절하는 식을 구성하였습니다.
4. Convergence Properties
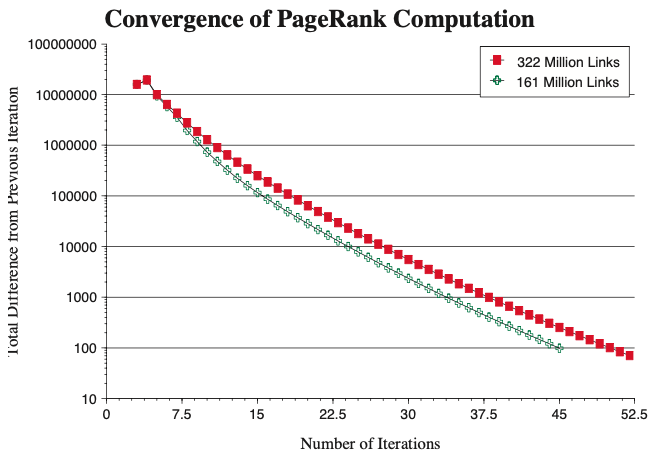
수렴은 어떤 식으로 진행되는가에 대한 실험에서, 322 million link 데이터베이스에 대하여 52번의 Pagerank 알고리즘 iteration으로 수렴하였다고 하며, 절반의 데이터에 대해서는 45번의 반복이 필요했다고 합니다. 즉, 데이터가 증가하여도 속도면에서는 부담이 되지 않음을 보여줍니다.
5. Searching with PageRank
5.1 Title Search
저자들은 PageRank를 사용하여, 제목기반 / 전체 검색어 기반 검색 엔진 두개를 개발하였으며, 후자가 Google입니다. PageRank의 대표적인 장점은, 불특정한 검색어에 대해서 우수하다는 것인데, 예를 들어 ‘Stanford University’를 검색했을 경우, 다른 알고리즘들은 Stanford를 담고 있는 모든 페이지를 먼저 내뱉었겠지만, PageRank는 정확히 학교를 return한다고 합니다.
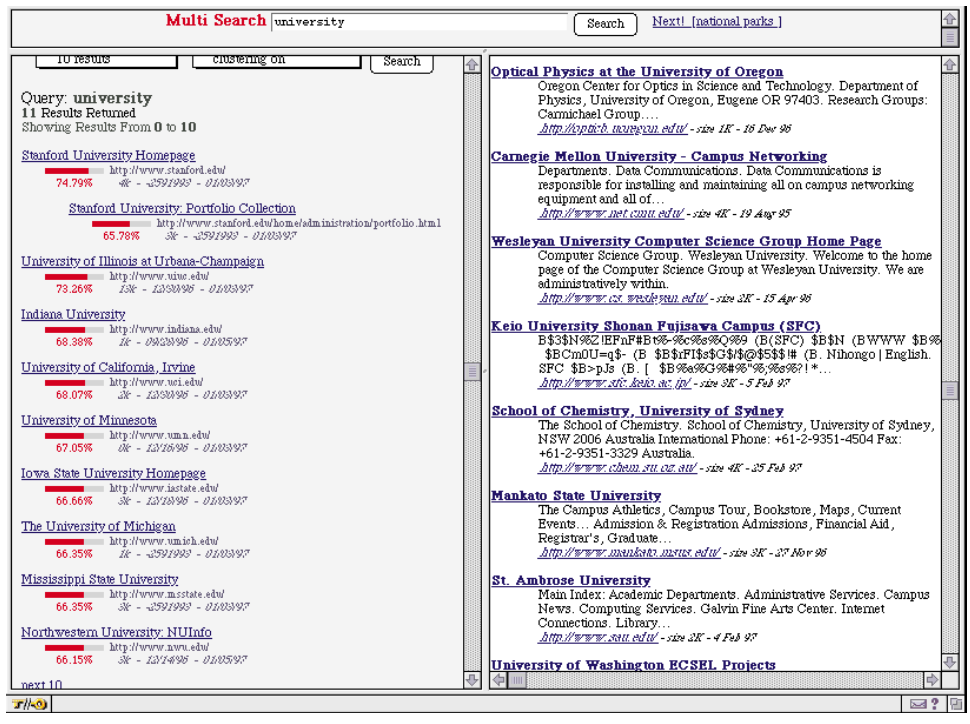
위의 이미지는 “University”를 검색했을 때의 결과이며, 왼쪽이 PageRank이며 오른쪽이 AltaVista라는 다른 검색엔진(이었던 것)이라고 합니다. PageRank의 결과는 대학 중의 대학인 Stanford를 먼저 보여주고(pagerank 1등), 나머지 대학들을 보여주는 반면, AltaVista는 Oregon의 대학부터 보여줍니다. Pagerank는 대학의 보이지 않는 서열 또는 영향력을 반영하여 결과를 보여주는 것을 알 수 있습니다.