Latent Dirichlet Allocation with Python Code Implementation

Posted on |

Latent Dirichlet Allocation

image-20201011190205573

참고 논문

이번 포스트에서는 Latent Dirichlet Allocation(LDA)에 대하여 알아보겠습니다.

LDA는 두 가지의 다른 개념이 LDA 라는 같은 축약어를 사용하는데, 신기하면서도 다행히도 두 기법 모두 ‘차원축소’의 기능을 갖고 있습니다.

  • Latent Dirichlet Allocation
  • Linear Discriminant Analysis (혼동을 위해 LDAs라고 표기하겠습니다)

LDAs는 PCA와 같이 주 기능이 차원축소입니다. 주 기능이라 함은, 물론 다른 상황에서도 쓰일 수 있지만 본연의 목적이라는 뜻입니다. 반면, LDA는 주 기능이 차원 축소라기보다는 Topic Modeling이며, Topic Modeling의 정의가 논문의 표현을 빌면 다음과 같기 때문에 차원축소와 유사한 역할을 하게 됩니다.

To find short descriptions of the members of a collection that enable efficient processing of large collections while preserving the essential statistical relationships that are useful

즉, 방대하고 다량의 문서를 간단한 설명으로 나타내는 것, 문서 내에서 그 문서를 나타낼 수 있는 ‘Topic’을 찾아내는 것이기에, 큰 차원을 작은 차원으로 줄이는 차원 축소의 역할을 할 수도 있습니다.

LDA를 사용함으로써 사용자가 살펴보고 싶은 내용은 다음과 같습니다.

  • 갖고 있는 문서들이 무슨 주제(Topic)을 이야기하고 있는가?
  • 하나의 문서는 무슨 주제(Topic)을 이야기하고 있는가?
  • 특정 주제(Topic)에 포함된 단어들은 무엇인가?
  • 특정 단어는 어떤 주제에 사용되는가?

이는 설명을 진행하면서 하나씩 풀어가게 될 것이며, LDA는 위의 내용을 자신들의 식에 의미적으로 반영하려고 많은 노력을 진행했습니다.

LDA는 이렇게 목적은 매우 간단합니다. 하지만 사용되는 수식과 그 수식의 배경 수식 등 물리고 물리는 개념들이 매우 많으며, LDA를 완벽하게 이해하고 있다면 Bayesian 통계나 확률에 대한 기본이 확고하게 자리잡고 있다는 뜻입니다. 따라서 LDA를 설명하는 자료들을 보면 어려운 개념을 최대한 빼고, 전체 골자를 전달하는 데에 많은 노력을 하는 듯합니다. 하지만 본 포스트에서는 원 논문인

“Latent Dirichlet allocation - David M. Blei, Andrew Y. Ng, Michael I.Jordan”

을 살펴보면서 조금 더 배경 및 깊은 원리를 살펴보고자 하는 것이 목적입니다. 하지만 저 역시도 기법의 난이도로 인하여 LDA의 A to Z 모두를 설명할 수는 없었습니다. 하지만 공부를 해가면서 느낀 점 중에, 논문에 나타난 개념을 쉽게 설명하려다 보니 꽤 중요한 개념들이 설명 자료들에서 사라져가고, 다른 설명 자료가 그것을 차용하면서 점차 당연하다듯이 기초 배경이 사라졌다는 것입니다. 따라서 저는 최대한 논문을 읽어가며 해당 포인트들을 많이 반영하려 노력할 것입니다. 이를 위해 논문의 순서를 최대한 반영할 생각이지만 중간중간 추가적인 설명이 필요한 부분은 가미하겠습니다.

그렇다면 먼저, LDA의 탄생 배경부터 살펴보겠습니다.

1. Introduction

LDA의 기원, Information Retrieval

LDA의 목적은 서문에서 설명한 바와 같이, 다량의 문서를 “간단하게” 표현하려는 것입니다. 이런 시도는 머신러닝 분야에서 먼저 시작한 것이 아닌 Information Retrieval(IR) 분야에서 먼저 시작하였습니다. IR에서 지향했던 바는 인터넷에 존재하는 다량의 문서를 “빈도”를 기반으로 간단한 숫자로 표현하는 거였습니다. 이를 위해 문서의 등장하는 단어의 단순한 빈도를 넘어, 전체 문서에서의 단어의 빈도를 반영한 수식인 TF-IDF의 개념을 사용하여 문서를 축약하고자 했습니다. TF-IDF를 통해 단순히 빈도가 높은 단어에게 높은 점수를 부여하는 것이 아니라, 단어가 등장하는 해당 문서에서 큰 영향력을 갖느냐의 정보도 반영할 수 있게 되었습니다.

TF-IDF

하지만 TF-IDF의 축소 능력은 그다지 크지 않았습니다. 따라서 이보다 우수한 성능을 보이기 위해 Latent Semantic Indexing(LSI)라는 기법이 나타났습니다. LSI는 단어 빈도와 문서를 행과 열로 나타난 Matrix에 Singular Value Decomposition(SVD)을 적용하여, 분산을 최대한 보존하고 있는 Subspace를 찾고자 했습니다. LSI를 사용하게 되면 TF-IDF의 선형 결합을 나타내는 것이라 하며, 동의어와 다의어의 관계도 파악할 수 있는 장점이 있다고 합니다.

하지만 LSI도 연구자들의 만족을 달성할 수 없어 Hofmann(1999)가 pLSI를 제시합니다. 실상 LDA의 원리에 가장 가까운 개념이 pLSI입니다. pLSI는 문서의 각 단어가 Topic의 Mixture Model(Multinomial)로부터 왔다는 가정을 가지며, 따라서 각 단어들은 단 하나의 주제로부터 생성되었다고 합니다. 즉, 하나의 문서에는 다양한 주제들로부터 온 단어들(Mixture Components)로 구성이 되어 있을 것이고, 해당 단어들의 주제를 분포로 나타내면, 문서의 주제 분포가 되는 것입니다. LDA를 조금이라도 공부해보신 분은 이 개념이 LDA와 매우 유사한 것이라고 느껴지실 겁니다. 하지만 LDA와 다르고, pLSI의 한계점이라고 치부하는 부분은, 단어들에 대한 직접적 주제할당은 가능하지만, 문서는 단어들로부터 주제가 도출된다는 간접적인 방식이라는 점입니다.

그렇다면 단어와 문서, 모두에 대한 확률 모델을 구축하는 방법이 있을까요? pLSI의 문제점을 극복하고자 탄생한 것이 LDA입니다.

2. Notation and Terminology

LDA 이전의 기법들에 대해서 알아보았으니, 이제 곧 LDA 기법의 절차를 알아봐야 합니다. 하지만 이전에 논문에서 Notation 정리를 한번 하고 진행하니 저도 따르겠습니다.

  • Word(단어): 하나의 문서에 포함된 단어들의 Index로 표현하여 V개의 단어가 있다면 ${1,…,V}$ 로 표현합니다. 하지만 단어들은 Discrete Data이므로 One-Hot-Encoding의 형태로 나타낼 것입니다. 논문에서는 다른 표현으로 설명하는데 결국에는 원핫인코딩을 표현한 것입니다. 이를 $w$로 표현하겠습니다.
  • Document(문서): 문서는 N개의 단어들의 Sequence입니다. 따라서 w = ${{w_1, w_2, w_3 … w_N}}$으로 나타납니다. w와 $w$가 매우 헷갈리는데, 이를 논문에서는 단순히 이탤릭체와 볼드체로 구분하고 있습니다.
  • Corpus(말뭉치): 말뭉치는 M개의 문서들의 집합입니다. 따라서 $D = {{w_1, w_2 … w_M}} $로 나타냅니다. 아래첨자를 쓰기 위하여 w가 $w$로 변하였는데 D 안에 있는 $w$는 문서입니다.

논문의 표현을 사용하면 설명을 할 때 불편할 것이므로, Word는 $w$, Document는 $d$, Corpus는 $c$ 로서 나타내겠습니다.

3. Latent Dirichlet Allocation

LDA: Generative probabilitstic model of a corpus

LDA는 Corpus에 대한 생성 확률 모델입니다. 생성을 한다는 뜻은 Corpus를 세상의 모든 단어라고 가정해보면, 해당 단어들을 사용해서 문서들을 생성한다는 뜻입니다. 또한 이를 다르게 표현해보면, 잠재되어 있는 Topic들의 분포를 통해 문서를 만들고, 각 Topic은 단어들의 분포로 이루어져 있다는 뜻입니다. 간단하게 예시를 들어보도록 하겠습니다.

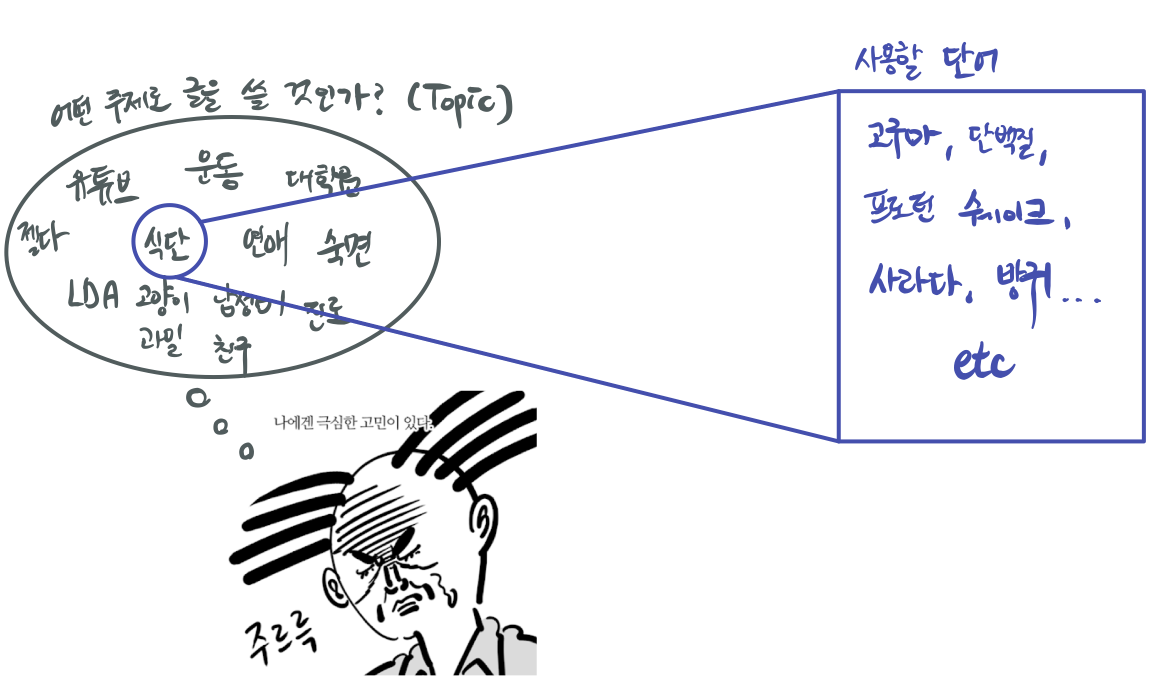
image-20201010235644890

삼말년이라는 한 작가가 빠르게 어떠한 주제로든 글을 작성해야 한다고 해보겠습니다. 따라서 자기가 평소에 흥미와 관심이 있는 주제를 ‘주제 분포’에서 고르고, 책상에 앉아서 글을 적다보면, 사용하게 되는 단어들은 당연히 해당 주제를 반영하게 될 것입니다. ‘식단’이라는 주제에 대하여 삼말년이 글을 작성한다고 하면, 식단을 설명하기 위한 고구마, 쉐이크, 샐러드 등과 같은 단어를 많이 사용하겠지요.

Mixture model

여기서 잠깐 짚고 넘어가야 하는 개념이 Mixture Model입니다. Mixture Model의 대표적인 예시는 Gaussian Mixture Model(GMM)이며, GMM은 보통 Clustering에서 많이 활용합니다. 즉, Mixture Model이라는 것이 본디 여러 개의 분포로 하나의 분포를 만들었을 때, 특정 데이터는 어느 분포에 속해있는가(Cluster)의 문제를 나타냅니다. 보통 Mixture Model은 Mixture Distribution과 많이 혼용해서 쓰는데 이 둘은 “목적” 자체가 다른 개념입니다.

  • Mixture Distribution: 하위집단으로부터 전체 집단의 특징들을 얻는 것
  • Mixture Model: 관찰된 집단이 주어졌을 때, 하위집단들의 특징들에 대한 통계적 추론

즉, GMM에서도 전체 분포에서 하위 집단(Cluster)를 파악하려는 것과 같이 LDA에서도 잠재되어 있는 Topic(Latent Topic)들이 존재한다고 가정할 때, 그 중 지금 바라보고 있는 문서는 어떤 하위 Topic에 속해 있을 지 판단하는 문제가 됩니다. 그리고 Latent Topic에 대한 분포를 Dirichlet 분포로 바라보겠다는 것이죠. 다시 한번 LDA의 이름을 따라가보자면,

Latent Dirichlet Allocation

$\Rightarrow$ Latent Topic Distribution을 Dirichlet으로 설정하여, Topic을 Allocation 하는 방법

을 뜻하는 것입니다.

Dirichlet Distribution (디리클레 분포)

디리클레 분포는 켤레사전 분포의 사후확률 분포입니다. 켤레사전 분포란 사후확률 분포 $p(\theta | x)$ 가 사전분포 $p(\theta)$ 와 같은 가족군으로 묶일 때 그 사전/사후확률분포를 모두를 나타내는 것입니다. 이 개념은 Bayseian 통계에서 Prior를 통해 Posterior를 Update를 할 때 활용이 되고, 사전 분포와 사후 분포가 같은 가족군에 묶여 있을 때, 계산이 용이해서 켤레 사전분포를 사용하는 것입니다. 식으로 나타내면

$P(\theta |X) = P(X|\theta) * P(\theta)$ 로 나타낼 수 있으며,

좌측 항에 있는 $P(\theta|X)$인 Posterior를 구해내는 것이 식의 진 목적입니다. 즉, 데이터들이 주어졌을 때, 파라미터의 확률 분포가 어떻게 나타날 지를 의미합니다. 우측 항에 있는 $P(X|\theta)$는 확률 분포가 주어졌을 때의 데이터의 분포, 그리고 $P(\theta)$는 파라미터의 확률분포를 나타냅니다. 식을 따라 말로써 정리해보면(우측 항부터),

(파라미터 확률분포)와 (해당 확률 분포일 때의 데이터의 분포)를 곱하면, (데이터가 존재할 때의 파라미터 분포)를 구할 수 있다 라는 표현으로 나타낼 수 있습니다. 이는 다시,

(Prior Distribution)과 (Likelihood)를 곱하면, (Posterior Distribution)을 구할 수 있다로 표현할 수 있으며, 이를 LDA의 (키네틱) 플로우에 적용해보면,

(사전에 정의한 Topic Distribution - [Prior] Dirichlet) * (Prior를 설정했을 때 단어들의 분포) =(단어들의 분포가 존재할 때, Topic Distribution- [Posterior] Multinomial) 로 나타낼 수 있습니다. 즉, Conjugate Prior / Posterior를 LDA에서 사용하는 데에는 위와 같은 명백한 이유가 있는 것입니다.

LDA Procedure

LDA는 전체 Corpus $c$로부터 각 Document $d$를 만들기 위하여 다음과 같은 절차를 따릅니다.

  1. Choose N ~ Poisson($\xi$)

  2. Choose $\theta$ ~ Dir($\alpha$)

  3. For each of the N words $w_n$:

    (a). Choose a topic $z_n$ ~ Multinomial($\theta$)

    (b). Choose a word $w_n$ from ${p(w_n|z_n, \beta)}$, a multinomial probability conditioned on the topic $z_n$

위와 같이 간단하게 나타낸 절차는 다음과 같은 부가사항이 존재합니다.

  • Dirichlet Distribution의 차원 $k$는 알려져 있고, 고정되어 있다 (디리클레 분포는 사전분포이니 사용자가 직접 설정하니 당연합니다).
  • $\beta$는 word probability인데, $k * V$ Matrix로 구성되어 있으며, 이는 (Topic 개수 * 단어 개수)의 Matrix인 것이다.
    사실 논문에 나타난 $\beta$는 의문점이 다소 존재하는 부분입니다. 그 이유는 다른 자료들에서는 $\alpha$ / $\beta$ 모두 Dirichlet Distribution의 Parameter이며, $\alpha$는 위에서 설명한 듯이 문서-토픽 분포를 조절하며, $\beta$ 는 토픽-단어 분포를 조절한다고 대개 설명하기 때문입니다. 하지만 만약 논문도 그런 의미로 사용하고 있었다면, $\alpha$와 묶여서 설명이 되어야 하는데, 그것이 아니라 행렬이라고 명시하고 있습니다. 따라서 제 생각에는 $\beta$ 자체가 Dirichlet Distribution으로서 $k*V$ 차원에서 $k$ 주제 만큼의 V 차원의 분포가 있다고 해석할 수 있겠습니다.
  • Poisson 분포는 사실 위 절차에서 큰 영향력을 안 갖기에 생략해도 된다. 이는 웹상에 존재하는 다양한 LDA 관련 자료만 살펴보아도 Poisson에 대한 설명은 대부분 생략되어 있습니다. 왜냐면 N은 문서의 길이를 나타내는 것인데, 실상 단어들의 길이는 Fixed된 것이 아니기 때문입니다.

Simplex

A $k$-dimensional Dirichlet random variable $\theta$ can take values in the $(k-1)$ simplex

논문의 표현을 그대로 가져온 위 문장은 k 차원의 Dirichlet 분포에서 추출한 Random Variable은 $k-1$ 차원의 Simplex위에 있음을 나타냅니다. 그런데 대체 Simplex란 무엇일까요? Simplex는 분야별로 다양한 정의가 존재하지만 확률론적인 해석은 “Space of all probabilities distributions with support N” 입니다. 그리고 k에 따라서 다음과 같은 Simplex를 정의할 수 있습니다.

  • 0-simplex는 점
  • 1-simplex는 lines segment
  • 2-simplex는 triangle

저도 아직 정확하게 와닿지는 않지만, 이것을 Dirichlet Distribution에 적용하는 법에 대해서 안내해드리겠습니다.

위에서 Dirichlet 분포에 대하여 언급할 때 놓친 부분이, Dirichlet은 ‘분포의 분포’ 라는 점입니다. 특히 Multinomial 분포들을 담고 있는 분포로서 여기서 분포들을 샘플링하는 것입니다. 시각화하여 보여드리기 가장 좋은 예시가 k = 3, 즉 2-Simplex로서의 Dirichlet 분포이니 살펴보겠습니다.

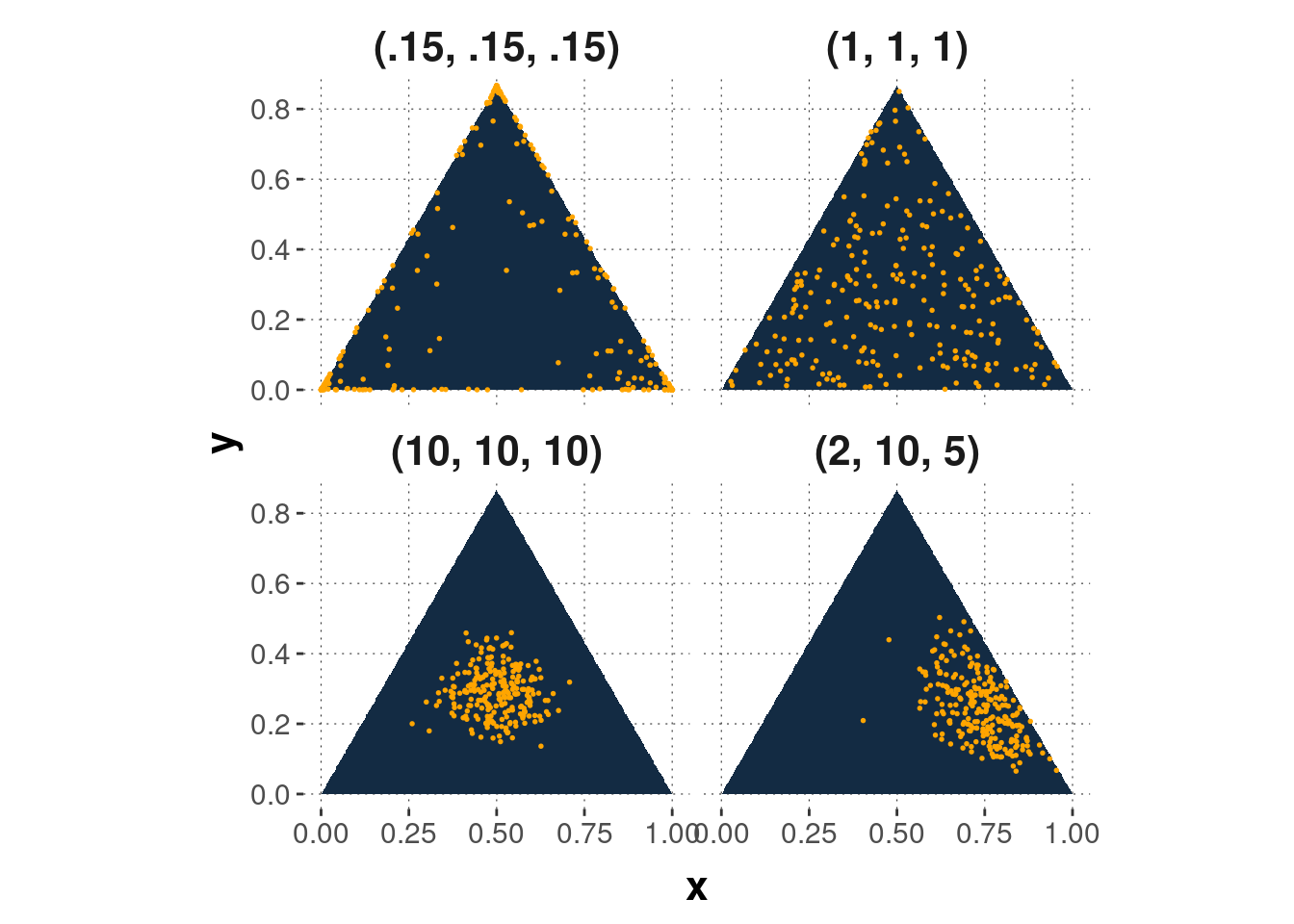
B.1 Selected continuous distributions of random variables | Introduction to Data Analysis

k가 3이라는 뜻은, 다루고자 하는 Topic의 갯수가 3개라는 뜻이며, 이 3개의 Topic에 대한 확률 Prior Distribution을 Dirichlet Distribution에서 가져오는 것입니다. 이 때, 삼각형의 Simplex로 3차원의 확률분포를 담을 수 있는 것입니다.

그리고 자세히 보면 삼각형 위에 숫자들이 보이시나요? 해당 숫자는

  • Choose $\theta$ ~ Dir($\alpha$)에서 살펴보았던 $\alpha$입니다.

LDA에서 사용하는 Dirichlet Distribution은 Symmetric한 것입니다. 즉, 하나의 $\alpha$ 가 몇 차원의 분포이든 동일하게 사용되게 됩니다. $\alpha$가 클수록 3차원의 확률분포가 중앙에 모여 즉 각 확률들이 동등한 값을 가지는 점들이 많아집니다. 반대로 $\alpha$가 작아지게 되면, 모두 흩어져서, 꼭지점에 각기 집합하게 되는데 이는 각 Topic들이 나타나는 확률이 하나의 Topic에 집중하게 되는 것입니다. 자신의 데이터의 꼴에 따라서 $\alpha$ 를 선택하는 것이 LDA를 더 현명하게 사용하는 길입니다.

참고자료: Simplex의 정의와 설명

LDA, as Bayesian Network

파라미터 $\alpha$, $\beta$가 존재할 때, Topic에 대한 mixture $\theta$와 N개의 topic z, 그리고 N개의 단어 w에 대한 Joint Distribution 식은 다음과 같이 표현할 수 있습니다.

$ p(\theta, z, w| \alpha, \beta) = p(\theta|\alpha) \prod_{i=1}^N p(z_n|\theta)p(w_n|z_n, \beta)$

우측에 있는 식을 읽어보면 이상하게도 잘 읽힙니다. 하지만 이렇게 결합분포를 해석해도 되는지, 너무 끼워맞추기 식이 아닌지에 대한 의문이 듭니다. 이를 읽어보면

$p(\theta|\alpha)$ $\alpha$가 주어졌을 때, $\theta$의 확률 $\alpha$가 주어졌을 때의 Dirichlet 분포 $\theta$
$p(z_n|\theta)$ $\theta$가 주어졌을 때, $z_n$의 확률 사전분포 $\theta$가 주어졌을 때의 단어의 Topic $z_n$
$p(w_n|z_n, \beta)$ $z_n, \beta$의 가 주어졌을 때 $w_n$의 확률 단어의 Topic이 정해졌을 때의 단어 자체

즉, 왼쪽에 있는 결합분포 $p(\theta, z, w| \alpha, \beta)$는 $\alpha$가 주어졌을 때 Dirichlet 분포 $\theta$ 에, Document내의 Topic $z_n$ 분포와 $w_n$을 곱하는 것입니다. 하지만 기존의 결합분포에 대한 Factorization은 다음과 같이 이루어집니다.

$p(x_1, x_2,…x_K) = p(x_K|x_1, …, x_{k-1})…p(x_2|x_1)p(x_1)$

즉 LDA에서 사용하는 결합분포에 대한 해석은 기존 Form이 아니라 다른 것이며, 이는 Bayesian Network로서 설명할 수 있습니다. 하지만 논문에서는 Bayesian Statistical Modeling, 즉 사전 / 사후분포로만 살펴보기 때문에 이해가 다소 안됐었던 부분이 있었습니다.

Bayesian Network는 카이스트의 문일철 교수님의 강의에서 자세히 나와있었는데 간략하게 설명해보겠습니다.

Bayesian Network는 방향성 그래프 모델로서 그래프의 링크들이 방향성을 갖고, 화살표로 표현한 그림을 그립니다. 이를 통해 화살표가 조건부 확률을 나타내게 됩니다. 다음은 저의 최근 심경 및 상태에 대한 Bayesian Network이며 이것으로 결합분포를 해결해보겠습니다.

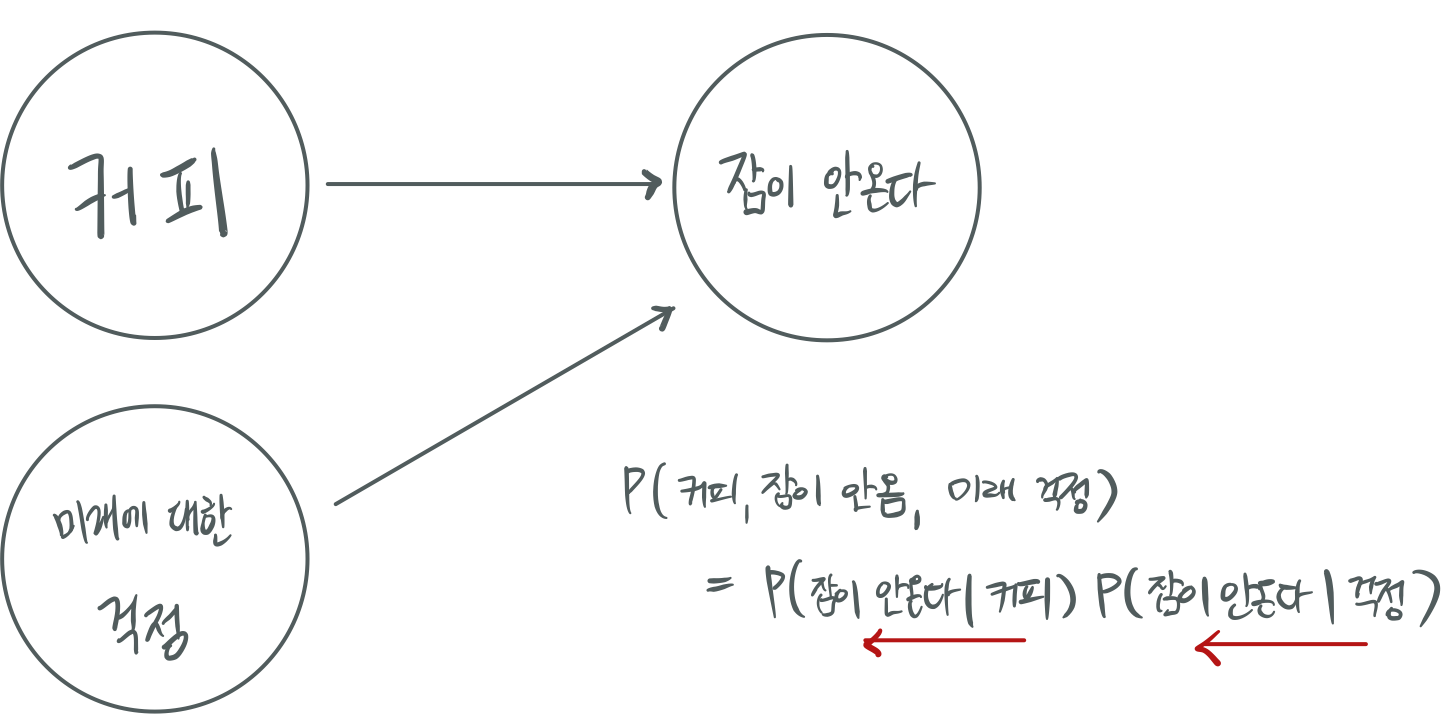
image-20201009230159714

즉 어떠한 다량의 변수들이 포함된 결합분포라 할지라도, Bayesian Network로서 표현이 되어져 있거나, 표현이 가능하다면 좀 더 쉽게 결합분포를 Factorize할 수 있는 것입니다. 그런데 위의 저의 심경에 대한 예시와 같은 표현이 LDA에서도 존재합니다.

Latent Dirichlet allocation - Wikipedia

해당 Plate Notation을 Bayesian Network라고 생각하여 $p(\theta, z, w| \alpha, \beta)$에 대한 결합분포를 해결하기 위한 원소들을 꺼내보면,

  • $p(\theta|\alpha)$
  • $p(z_n|\theta)$
  • $p(w_n|z_n, \beta)$

를 표현해낼 수 있습니다.

최종 식에 대한 정리 with Luis Serrano

LDA에 대한 ‘직관적인’ 이해가 잘 되지 않았을 때, 본 유튜브 영상을 보고, LDA의 총체적인 그림을 그려볼 수 있었습니다. Luis Serrano라는 분께서 LDA의 Generative Model에 대한 정리를 그림으로 통해 잘 설명한 것 같습니다.

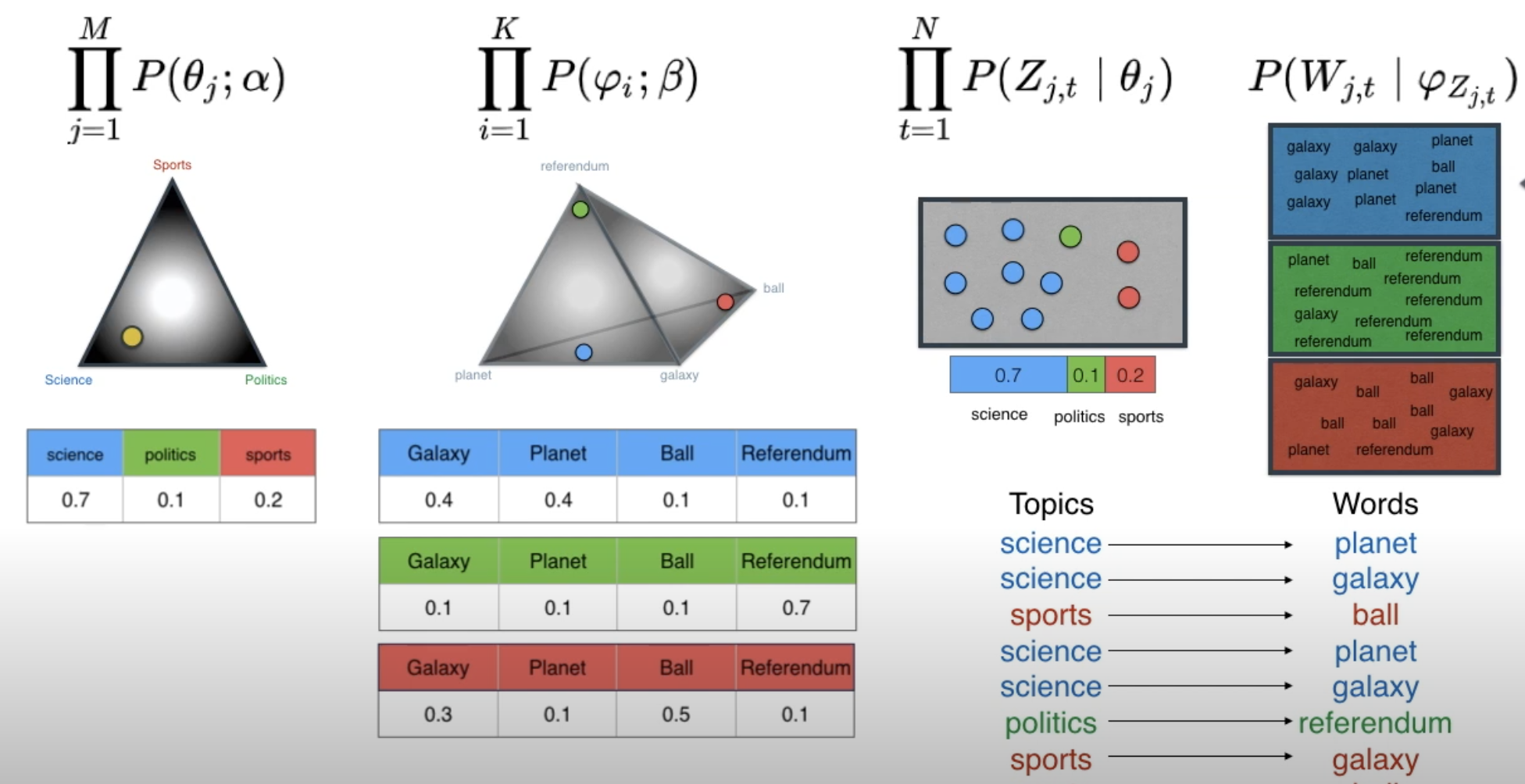
image-20201010174702662

위에서 LDA의 Generative Model의 Joint Distribution은 다음과 같이 표현할 수 있다고 했습니다.

$ p(\theta, z, w| \alpha, \beta) = p(\theta|\alpha) \prod_{i=1}^N p(z_n|\theta)p(w_n|z_n, \beta)$

하지만 본 영상에서는 $\beta$ 가 파라미터이며, 해당 파라미터를 사용하는 $\varphi$ Dirichlet 분포를 명확하게 나타냅니다 (원래 논문에서는 등장하지 않는 수식이며, 제 추측으론 이후의 등장하는 후속 연구들에서 이 과정을 포함하지 않았나 싶습니다). 그리고 구하고자 하는 값을 전체 Corpus $c$에 대한 식으로 변환하게 된다면,

$p(C|\alpha, \beta) = \prod_{j=1}^MP(\theta_j;\alpha)\prod_{i=1}^KP(\varphi_i; \beta) \prod_{t=1}^NP(Z_{j,t}|\theta_j) P(W_{j,k}|\varphi_{Z_{j,k}})$

로 나타낼 수 있습니다.

새로 나타나게 된 식을 설명하자면,

  • $\prod_{j=1}^MP(\theta_j;\alpha)$: $\alpha$를 통해 생성된 디리클레 분포에서 Topic 분포 $\theta$를 구하고,
  • $\prod_{t=1}^N P(Z_{j,t}|\theta_j)$: 획득한 Topic 분포 $\theta$에서 Topic $Z$를 구하고,
  • $\prod_{i=1}^KP(\varphi_i; \beta)$: $\beta$를 통해 생성된 디리클레 분포에서 Topic의 Word 분포 $\varphi$를 구하고,
  • $P(W_{j,t}|\varphi_{Z_{j,t}})$: 획득한 Topic의 Word 분포 $\varphi$를 통해 Word W를 구한다!

4. LDA and exchangeability

Exchangeability

“LDA의 성공 비결은 무엇입니까?” “Exchangeability입니다…”

LDA의 이론적 배경은 Bayesian Statistic, Mixture Model 등 다양합니다. 하지만 그 중 가장 Fundamental하여 논문의 하나의 장으로서 작성된 이론은 De Finetti의 Exchangeability입니다.

${z_1, z_2, …,z_N} $와 같이 random variable들이 존재할 때, 이들의 순서를 다양하게 섞었을 때의 확률이 원래의 형태와 같은 경우, 또한 어떤 순서로 섞어도 항상 같은 경우 Exchangeability가 존재한다고 할 수 있습니다. 이를 식으로 표현하면,

$p(z_1, …, z_N) = p(z_{\pi(1)}, …, z_{\pi(N)})$ where, $\pi$ is permutation

과 같이 나타낼 수 있습니다. 그리고 무한한 random variable의 sequence에서 subsequence들이 모두 exchangeable하다면 전체도 exchangeable합니다.

처음에 이 개념을 마주했을 때 와닿지 않은 이유는 원래부터 $p(a,b,c) = p(b,a,c) = p(c,a,b)$와 같이 확률 내부의 인자를 결합분포 내에서 바꾸어도 똑같기 때문입니다. 하지만 문장 내의 단어들의 Sequence를 나타낸 결합분포인 $p(w_1, …, w_N)$ 는 사실 순서가 반드시 보장되어야 하는 확률입니다. 예를 들어보면,

$p(우리, 팀의, 정글은, 쓰레기다) \neq p(팀의, 우리, 쓰레기다, 정글은)$이며, 이는 순서에 따라 확률이 달라진다는 것입니다.

De Finetti’s Theorem

De Finetti 정리는 Exchangeability를 활용해 다음과 같은 정리를 제시했습니다.

$p(X_1, X_2, …, X_N) = \int (\prod_{i=1}^Np(X_i|\theta))d\pi(\theta)$

이 정리를 통해 결합분포를 매우 간단하게, 결합분포를 구성하는 인자 $p(X_i|\theta)$들의 곱들로 표현할 수 있게 되어, $\theta$가 주어졌을 때, 해당 분포($\theta$)로 부터 나타난 random variable들은 모두 독립이고 동일한 분포한다는 것을 알 수 있습니다.

그럼 왜 이것이 LDA의 가정에 포함되었을까요?

LDA에서도 역시 순서를 무시합니다. 즉, 단어들의 순서를 무시하는 것이지요. 위의 문장의 예시에서 $p(우리, 팀의, 정글은, 쓰레기다) \neq p(팀의, 우리, 쓰레기다, 정글은)$가 아니라 같게 되는 것입니다. 그 이유는 Bag of words 가정을 갖고 있기 때문에 전체 Corpus내의 Word는 하나의 Bag에 포함되어 있기에 순서가 무시되게 되어, Exchangeability가 가능하게 됩니다. 이로 인해 계산상의 이점을 가지는 부분이 있는데 LDA의 Model인

$ p(\theta, z, w| \alpha, \beta) = p(\theta|\alpha) \prod_{i=1}^N p(z_n|\theta)p(w_n|z_n, \beta)$

입니다. 여기서 $\prod_{i=1}^N$가 수혜를 받는 부분입니다. 사실 Bayesian Network를 사용해도 $\prod_{i=1}^N$에 대한 이론적 보장은 할 수 없었습니다. 하지만 하나의 문서 내의 단어들, Topic들이 Exchangeable하다는 사실을 알았으니, 문서 내에서의 확률들을 결합분포로 적지 않고 수많은 곱셈으로 나타낼 있는 것입니다.

$ p(\theta, z, w| \alpha, \beta) = p(\theta|\alpha) p(w_n,z_n,d)$ $\Rightarrow$ $ p(\theta, z, w| \alpha, \beta) = p(\theta|\alpha) \prod_{i=1}^N p(z_n|\theta)p(w_n|z_n, \beta)$

5. Relationship with other latent variable models

본 섹션에서는 LDA와 다른 더 간단한 latent variable model을 비교해보고자 합니다

Unigram / Mixture of Unigrams, pLSI

Unigram model

Unigram model은 언어모델 중에서 가장 간단한 모델이라 할 수 있습니다. 각 단어가 서로 독립이라고 가정하고 결합분포를 확률의 곱셈으로 구하는 과정입니다.

$P(w_1, w_2, …w_n) = \prod_{i=1}^nP(w_i)$ or $P($Words in Document$) = \prod_{n=1}^Np(w_n)$

즉, 각 단어들이 단일한 Multinomial Distribution에서 추출되는 과정을 보이는 것입니다.

Mixture of unigrams

Unigram들의 Mixture는 (Unigram + random topic variable $z$)와 함께 구성됩니다. 즉, 각 문서는

  1. Topic $z$를 먼저 고른 뒤,
  2. Conditional Multinomial $p(w|z)$에서 N개의 단어를 독립적으로 추출합니다.

고로 식은 다음과 같이 구성됩니다.

$p(d) = \sum_z p(z)\prod_{n=1}^N p(w_n|z)$

즉 $p(z)$가 weight로 나타나고 $\prod_{n=1}^N p(w_n|z)$ 부분이 하위 모델의 역할을 하게 됩니다. Mixture of unigrams은 하나의 Document에는 하나의 Topic만이 존재한다고 가정을 하며, 따라서 $p(d)$ 로 나타나는 단어의 Distribution은 결국 Topic을 표현하는 방식이 됩니다.

image-20201010124658433image-20201010125008855

위의 그림에서 좌측의 Topic Multinomial Distribution이 $p(z)$를 표현한 것이며, 선택된 z의 $p(w|z)$를 우측의 Multinomial Distribution이 표현하게 됩니다. 하지만 Mixture of unigrams에서는 $\sum_zp(z)$ 부분에서 각 토픽에 대해서 하나씩 규합하기 때문에 Single Topic을 표현하게 되며, LDA는 이와 다르게 하나의 Document 내에 다중의 Topic들이 포함되도록 식을 구성하게 됩니다.

6. Inference and Parameter Estimation

지금까지, Latent topic model에 대하여 알아봤습니다. 즉, 하나의 문서 및 Corpus가 어떻게 생성되는 지 나타낸 것입니다. 하지만 여기까지의 절차는 Topic Modeling이 아닙니다.

우리가 실질적으로 Topic Modeling이라는 목적을 마주했을 때, 손에 쥐어져 있는 것은 뭘까요? 바로 문서들입니다. 문서들만이 존재하고 해당 문서들에 포함된 단어의 빈도수 정도가 저희 수중에 있습니다. 즉 $\theta, z$는 저희가 알 수 없으므로, Inference를 통해 해당 파라미터들을 추론해 나가고, Update를 하면서 갖고 있는 문서들의 Topic들이 어떻게 구성되어 있는지 알아야 합니다. 애초에 Latent라는 단어를 생각해보면 ‘숨겨져’있기 때문에 이것들을 파악해가는 과정이 Latent Dirichlet Allocation입니다.

$\theta, z$는 Hidden variable 또는 Latent Variable입니다. 즉 $w$를 제외하고는 아무것도 가시적인 것이 없습니다. 이를 파악하기 위한 Posterior Distribution을 구하는 식은

$p(\theta, z | w, \alpha, \beta) = \frac{p(\theta, z, w|\alpha, \beta)} {p(w|\alpha, \beta)}$ 입니다.

하지만 논문 및 다양한 자료들에 따르면 본 식을 계산하여 Estimation하는 것은 Intractable, 즉 불가능하다고 합니다. 따라서 이를 우회하는 방식인 approximation 기법으로 계산합니다.

논문에 나타나 있는 Approximation의 기법은 ‘Variational Inference’입니다. Variational Inference는 아직 실력이 부족하여 완전한 이해를 할 수가 없지만, 지향하는 바는 Jenkin’s Inequality를 통해, Lower Bound를 정하는 것이라고 합니다. 허나 역시 안 쓰는 데에는 이유가 있을 만큼 복잡해보이는 수식들이 즐비했습니다.

이보다 덜 복잡한 수식과 간단한 구현이 가능한 Gibbs sampling을 설명하겠습니다.

(Collapsed) Gibbs Sampling

Gibbs Sampling이 시작되면, 더 이상 확률 문제를 푸는 것 같지 않고 빈도적인 계산을 지속적으로 Update하는 과정이 이루어져 문제가 간단해집니다. Approximation 기법 중에서 가장 쉽고 확실한 방법이라 다른 여타 Approximation 기법보다 많이 쓰이며, Python으로 구현된 lda 역시 Gibbs Sampling을 적용해서 구현되었다고 안내하고 있습니다.

그럼 Gibbs Sampling에 대한 설명을 시작하겠습니다.

Gibbs sampling은 은근히 수식 계산이 많이 포함되며, 이를 하나씩 Line by Line 설명을 제가 하기보다는 강필성 교수님의 Topic Modeling - Part 3 를 시청하시는 것이 더 나을 것입니다. 따라서 저는 간략한 개념만 다룰 것이며, 이에 대한 코드 구현을 함께 살펴볼 것입니다.

Gibbs sampling의 기본적 골자는 “다른 변수들을 고정하고 한 변수만을 변경하면서 Update를 하면, 자동적으로 모든 변수들이 Update된다”입니다. 이 골자를 기반으로 기초적으로 구하고자 하는 분포는,

$p(z_i = j|z_{(-i)}, w)$

입니다. 이는 문서 내의 i번째 단어의 토픽 정보를 지운 뒤에 i번째의 단어의 토픽이 j 일 확률을 나타냅니다. 이를 도출해내기 위하여, 토픽 정보를 지운 뒤에, 남아 있는 토픽 분포 중에서 가장 확률이 높은 토픽을 지워진 토픽 정보에 넣습니다. 이런 과정을 EM 알고리즘처럼 반복하다보면, 최적의 Topic Distribution으로 수렴하게 됩니다.

그런데 여기서 의문은 Topic Modeling은

  • $\theta$: 문서 내의 Topic Distribution
  • $\varphi$: Topic 내의 단어 Distribution

을 구하는 과정인데 왜, z, 즉 단어의 Topic만을 관심 대상으로 iteration을 할까요? 실질적인 위의 두 분포에 대한 직접적인 계산이 이루어져야 하는 것 아닐까요?

이는 z를 Gibbs sampling과 같은 절차로 구하다보면 자동적으로 진 목적인 위의 두 분포가 도출되기 때문입니다. Corpus 내의 모든 단어들에 대한 z 를 구하게 되면 각 단어들의 Topic을 아는 것입니다. 그렇게 되면, 문서 하나씩의 단어들의 Topic들을 구해서 Topic Distribution($\theta$)을 구할 수 있으며, 마찬가지로 Topic 하나를 골라서 포함된 단어들의 분포를 구하면 $\varphi$를 구할 수 있습니다. 그리고 여기서 제목에서 나타난 (Collapsed)의 등장에 대하여 생각해볼 수 있습니다. $\theta$ / $\varphi$에 대한 Inference를 하는데 이 두 변수들이 Collapsed되어 구할 필요가 없어지고, z로만 계산을 이어나가기 때문입니다.

여러 복잡한 수식을 거쳐 결국 다음과 같은 최종 식이 도출되게 됩니다.

image-20201010190238557

해당 수식을 통해 어떻게 Update가 진행이 되고 결론에 도달하는 지 코드를 통해 살펴보고자 합니다.

Coding LDA with Gibbs Sampling from scratch

본 포스트에서 사용한 코드는 저의 github에 푸시했으니 참고해주시길 바랍니다.

1. Read Sample Data

구현을 함에 있어 영문으로, 그리고 안정적이고 전처리가 잘 되어 있는 sklearn의 news dataset을 사용하였습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
n_samples = 1000

data, _ = fetch_20newsgroups(shuffle=True, random_state=1,
                             remove=('headers', 'footers', 'quotes'),
                             return_X_y=True,
                            )
# 전체 데이터에서 1000개만 사용
data_samples = data[:n_samples]

# 데이터 내에 존재하는 단어에 대한 빈도(Count)를 계산하면 용량이 매우 커지기 때문에
# Sparse Matrix를 효율적으로 보존하는 CountVectorizer 사용
tf_vectorizer = CountVectorizer(max_df=0.95, min_df=2,
                                max_features=10000,
                                stop_words='english')
tf = tf_vectorizer.fit_transform(data_samples)

# 단어에 대한 index 설정
vocabulary = tf_vectorizer.vocabulary_

저희가 사용하게 될 데이터의 Sample을 하나 살펴보면

image-20201010202516623

다음과 같이 나타나게 됩니다. 그리고 vocabulary는 단어에 대한 index를 매겨 놓은 것이기에 다음과 같은 꼴을 가집니다.

image-20201010202646804

2. Document Initialization

다음으로는 본격적인 계산에 앞서, 문서들을 전처리 합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
documents = []

# tf.toarray()에 담겨있는 문서들을 하나씩 순회하면서
for row in tf.toarray():

    # count가 0이 아닌 index를 파악 > present_words
    present_words = np.where(row != 0)[0].tolist()
    present_words_with_count = []

    # present_words에 담겨 있는 index(count가 0이 아닌 index)에 대하여
    for word_idx in present_words:
        # 실제 count를 구하고 count만큼 index를 담는다.
        for count in range(row[word_idx]):
            present_words_with_count.append(word_idx)

    documents.append(present_words_with_count)

tf는 위에서 단어들의 빈도를 담아둔 Sparse Matrix이기에 이를 toarray()를 통해 풀어 헤칩니다. tf.toarray()는 매우 큰 Matrix로서 행은 하나의 Document를 나타내고, 열은 단어의 빈도를 담고 있습니다. 따라서 하나의 row의 1번 열은 1번으로 index되어 있는 단어의 빈도수를 나타냅니다.

다음 present_words에서는 빈도수가 0이 아닌 단어의 index를 가져오고 해당 단어의 빈도수만큼 present_word_with_count에 담습니다. present_word_with_count는 다음과 같이 나타나며, index들을 갯수만큼 담게 되어, 4203 index를 갖는 단어는 4번 담기게 됩니다.

image-20201010203445673

3. Parameter initialization

이제 문서들이 원하는 꼴로 준비가 되었으니 파라미터를 Initialize해보겠습니다. 저희가 필요한 파라미터는

  • D = 문서 갯수
  • V = 단어 갯수
  • T = 토픽 갯수
  • Alpha, Beta = 1 / Topic 갯수

입니다. 그리고 최종 식을 계산하기 위하여 필요한 분포는

  • document_topic_dist = 문서 내의 토픽 분포
  • topic_word_dist = 토픽 내의 단어 분포
  • document_words_cnt = 전체 문서별 단어 갯수
  • topic_words_cnt = 전체 토픽별 단어 갯수
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
D = len(documents)   # 문서 갯수
V = len(vocabulary)  # 고유 단어 갯수
T = 5               # 토픽 갯수

alpha = 1 / T        # 문서 내의 토픽에 대한 디리클레 분포 파라미터
beta = 1 / T         # 토픽 내의 단어에 대한 디리클레 분포 파라미터


# 문서들을 Input으로
def parameter_initialization(documents):
    # document 하나씩 길이에 따라서 단어들의 Topic을 반영할 준비를 word_topic_in_document에 해둔다.
    word_topic_in_document = [[0 for _ in range(len(document))] for document in documents]  # z_i_j

    document_topic_dist = np.zeros((D, T))   # 문서 내의 Topic Distribution
    topic_word_dist = np.zeros((T, V))       # 토픽 내의 Word Distribution
    document_words_cnt = np.zeros((D))       # 전체 Document의 단어 갯수
    topic_words_cnt = np.zeros((T))          # 전체 Topic의 단어 갯수

    for document_index, document in enumerate(documents):
        # 모든 문서 내의 단어들을 하나씩 순회하면서
        for word_index, word in enumerate(document):
            # 일단 Random Function을 사용해 Topic 갯수로 지정한 T개만큼의 Topic을 Random 배정
            word_topic_in_document[document_index][word_index] = random.randint(0,T-1)

            # 배정한 Word_topic
            word_topic = word_topic_in_document[document_index][word_index]

            # document 내의 topic 분포를 알기 위하여, 배정된 Topic을 하나씩 더한다.
            document_topic_dist[document_index][word_topic] += 1
            topic_word_dist[word_topic, word] += 1

            topic_words_cnt[word_topic] += 1
            document_words_cnt[document_index] += 1

    return document_topic_dist, word_topic_in_document, topic_word_dist, document_words_cnt, topic_words_cnt

document_topic_dist, word_topic_in_document, topic_word_dist, document_topic_dist,topic_words_cnt = parameter_initialization(documents)

위와 같은 절차를 통해 원하였던 파라미터와 분포를 계산해낼 수 있었습니다.

4. Gibbs Sampling

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def gibbs_sampling(init):
    document_topic_dist, word_topic_in_document, topic_word_dist, n_d, n_z = init
    for iteration in tqdm(range(10)):
        for document_index, document in enumerate(documents):
            for word_index, word in enumerate(document):
                word_topic = word_topic_in_document[document_index][word_index]

                # 해당 단어를 모든 분포 내에서 하나씩 임시로 뺀다.
                document_topic_dist[document_index][word_topic] -= 1
                topic_word_dist[word_topic, word] -= 1
                n_z[word_topic] -= 1

                # Update Process: 새로운 Topic을 단어에 반영하는 절차
                document_topic_expectation= (document_topic_dist[document_index] + alpha) / (n_d[document_index] - 1 + T * alpha)
                topic_word_expectation = (topic_word_dist[:, word] + beta) / (n_z + V * beta)
                new_topic_dist = document_topic_expectation * topic_word_expectation
                new_topic_dist /= np.sum(new_topic_dist)

                # 새롭게 구성된 분포에서 확률이 높은 값의 index
                new_topic = np.random.multinomial(1, new_topic_dist).argmax()

                word_topic_in_document[document_index][word_index] = new_topic
                document_topic_dist[document_index][new_topic] += 1
                topic_word_dist[new_topic, word] += 1
                n_z[new_topic] += 1

    return document_topic_dist, word_topic_in_document, topic_word_dist, n_d, n_z

Gibbs sampling은 빈도를 활용하여 Update하는 과정이라고 설명드렸습니다. 그리고 문서 내의 단어 하나를 뺀 뒤에, 해당 단어가 없을 때의 토픽 분포를 통해 재할당을 한다고 했습니다. 따라서 위의 Gibbs Sampling 코드에서도

  • 단어와 해당하는 토픽에서 1씩 빼는 과정
  • 차감한 단어와 토픽이 없는 상태의 분포를 통한 재할당
  • 다시 단어를 원래대로 돌려놓기

의 과정이 반영되어 있습니다. 특히 여기서 눈여겨 봐야 할 부분은 새로운 분포를 계산하는 부분입니다.

1
2
3
4
5
6
document_topic_expectation= (document_topic_dist[document_index] + alpha) / (n_d[document_index] - 1 + T * alpha)
topic_word_expectation = (topic_word_dist[:, word] + beta) / (n_z + V * beta)
new_topic_dist = document_topic_expectation * topic_word_expectation
new_topic_dist /= np.sum(new_topic_dist)

new_topic = np.random.multinomial(1, new_topic_dist).argmax()

image-20201010190238557

해당 파트가 Topic Weight를 계산하는 부분입니다. 그런데 처음에 제가 이 개념을 마주했을 때는, 분수식으로 작성되어 있었기 때문에, 결과 값이 상수라고 오해했습니다. 하지만 본 코드를 통해 문서에 대한 토픽 가중치와 토픽에 대한 단어 가중치가 모두 array, 즉 분포로서 나타남을 확인할 수 있었습니다. 그리고 마지막 Line에 새로운 분포에서 Multinomial 중 최대의 값을 뽑아냄을 보이고 있습니다.

5. Result

데이터를 읽고, 파라미터를 초기화하고, 깁스 샘플링을 한 결과를 다음과 같이 나타낼 수 있었습니다.

1
2
3
4
5
6
inv_vocabulary = {v: k for k, v in vocabulary.items()}
n_top_words = 10
for topic_idx, topic in enumerate(topic_word_dist):
    message = "Topic #%d: " % topic_idx
    message += " ".join([inv_vocabulary[i] for i in topic.argsort()[:-n_top_words - 1:-1]])
    print(message)

image-20201010210716411

Topic에 가장 빈도가 높은 단어들을 10등에서 끊어서 나타낸 결과입니다. Topic #3을 살펴보면 israel, government와 같이 국가와 정부에 관한 Topic임을 알 수 있으며, Topic #4 같은 경우는 edu, graphics, ftp, file 등과 같이 어떤 문서 작업에 관한 Topic임을 추론할 수 있습니다.

이 결과는 Gibbs Sampling의 iteration을 10번만 진행하고 Topic을 5개만을 지정한 결과였습니다. 이번에는 iteration을 100번 진행하고 Topic을 20개로 늘려서 진행해보겠습니다.

image-20201010212012337

Iteration 결과 Topic들에 포함된 단어들을 통해서 해당 토픽이 무슨 이야기를 하고 있는지에 대한 파악이 더 용이해졌습니다.

  • Topic #0, #1: 컴퓨터
  • Topic #4: 수학
  • Topic #10: 게임
  • Topic #11: 이스라엘
  • Topic #18: 무기, 전쟁

이로써 Gibbs Sampling에 대한 구현으로 Topic에 포함된 단어들이 어떻게 나타나는 지 살펴볼 수 있었습니다. 확률 분포를 구하는 과정을 수식으로 배우다보면, 항상 미분 적분과 같은 수학적인 절차만 필요하다고 착각할 수 있는데 확률 분포라는 것이 본디 빈도로부터 도출되는 것인 것을 다시 한 번 Gibbs Sampling으로서 확인할 수 있는 시간이었습니다.