AutoEncoders

맨 처음 문장에서 AutoEncoder의 정의를 설명하지만 다소 와닿지 않은 부분이 있었습니다.

Autoencoder is a neural network tha is trained to attempt to copy its input to its output

원래 알고 있던 AutoEncoder는 중간의 Hidden Layer로 축소 / 확장 시킨 뒤, 다시 원 상태로 복구시키는 것인데, Copy라는 말이 위의 절차를 생략한 채 진행되는 것처럼 보이기 때문입니다. 하지만 원칙적으로 보면 Input과 Output이 동일하니 Copy를 하는 것이 맞다는 생각도 들었습니다.

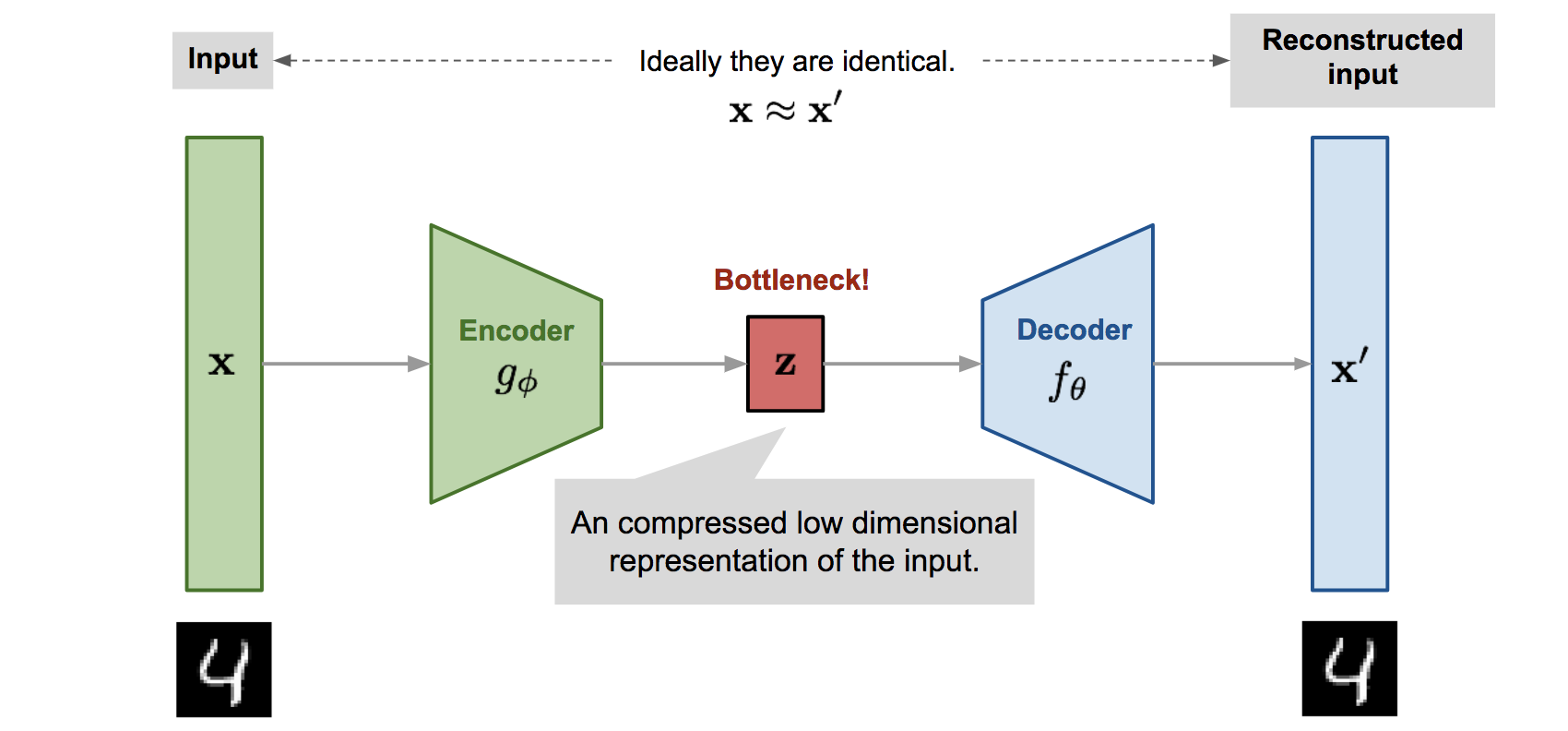
Autoencoder를 수식으로 살펴보면,

$h = f(x)$: Input $x$를 hidden layer $h$로 변환
$r = g(h)$: Hidden Layer $h$를 reconstruction $r$, 또는 $x$로
다시 재구성하는 과정

으로 나뉘게 됩니다. 하지만 만일 Autoencoder가 $g(f(x)) = x$의 역할, 즉 Input을 다시 Input으로 바꾸는 과정만을 담고 있다면 무의미한 활동이 될 것이며 활용도가 없습니다. 따라서 Input의 근사치, 또는 Training Data와 유사한 데이터를 복원하려하며, 이런 과정을 통해서 Input의 어떤 면모를 학습할지 선택하게 됩니다.

최신 Autoencoder는 이런 Encoder와 Decoder를 단순히 Deterministic Function으로 바라보지 않고, 더 나아가 Stochastic Function으로 나타내어,

$h = f(x)$: Input $x$를 hidden layer $h$로 변환 $\Rightarrow p_{encoder}(h|x)$
$r = g(h)$: Hidden Layer $h$를 reconstruction $\Rightarrow p_{decoder}(h|x)$

로서 나타내기도 합니다. 이런 관점은 Autoencoder가 전통적으로는 차원 축소에서 많이 활용되었던 반면, Generative Model로의 발전으로 이어지게 하였습니다.

Autoencoder는 또한 Neural Network(NN)의 일종이기 때문에, Parameter Update를 위해 NN에서 활용하는 Mini-batch Gradient Descent, Back Propagation등의 기법을 활용합니다.

Undercomplete Autoencoders

Autoencoder에서 Decoder부분은 사실 중요한 부분이 아니며, 단순히 중간 Hidden Layer인 $h$를 생성하기 위하여 거드는 역할 정도를 합니다. 즉, Autoencoder를 훈련시킴으로써 Input을 Output으로 Copy하는 과정 속에서 유용한 Feature를 Extract하고자 하는 것이 목적입니다.

$h$를 저차원으로 줄이자

AE를 통해 유용한 Feature를 뽑아내는 방법 중 하나는 Input보다 차원을 줄이는 것이며 이를 Undercomplete라고 합니다. 이를 통해 자동적으로 훈련 데이터의 Salient한 Feature를 뽑아낼 수 있도록 하며,

Loss Function = $L(x, g(f(x)))$

를 최소화 하는 과정으로 최적화를 진행합니다. 이 때 Decoder가 Linear하고 $L$ 함수가 MSE로 지정된다면, Undercomplete Autoencoder는 PCA와 같은 Subspace를 학습한다고 합니다. NN으로 Encoder / Decoder를 지정하면 Non-Linear Function인데 이를 Linear로 사용하는 경우를 말합니다. 즉, Non-Linear Function을 통해 학습을 한다는 것은 PCA의 일반화를 뜻하게 됩니다.

하지만 이는 Encoder / Decoder의 Capacity가 지나치게 높을 때 문제가 되며, Input을 저차원으로 줄이는 것이 Enc / Dec Function의 Capacity를 모두 담지 못하게 되어 $h$가 유용한 정보를 담기 위한 충분한 그릇이 되지 못할 수 있습니다. 즉 Under-complete는 차원 축소가 가능하지만 Autoencoder의 강력함을 견뎌내지 못할 수 있다는 것입니다.

$h$를 동차원, 또는 고차원으로 늘리자

$h$가 Input의 차원보다 더 클 경우는 Overcomplete라고 칭합니다. 위에서 Under Complete가 유용한 $h$를 생성해내지 못할 수 있다고 했으니 Overcomplete인 경우에는 이 문제가 해결될까 싶었지만 아니었습니다. 해당 경우에는 Capacity가 낮은 함수인 Linear Function을 Enc / Dec로 사용했을 경우에도 $h$의 유용성을 보장할 수 없습니다.

이상적으로 봤을 때,

Enc / Dec Capacity
Code dimension ($h$)

를 적당히 조정하는 것으로 AE를 성공적으로 구축해낼 수 있으며, 해당 방법이 Regularized Autoencoder(RAE)입니다.

RAE는 Enc / Dec를 Shallow하게, 또는 Complexity를 낮게 구성하거나 $h$ 차원을 줄이는 방법 대신! Loss Function을 사용하여 단순히 Input을 Copy하는 것보다 더 많은 것을 학습하도록 합니다. 이에는

Sparsity of the representation
Smallness of the derivative of the representation
Robuestness to noise or to missing inputs

로 나타냅니다. 이를 통해 RAE는 함수의 Capacity나 Code Dimension의 조화에 대한 고려 없이, Non linear Function 사용, Overcomplete를 자유자재로 사용하면서 데이터 분포에 대한 유용한 정보를 생성해낼 수 있습니다.

Sparse Autoencoders

Sparse Autoencoder(SAE)는 $h$에 대하여 직접적인 정규화를 진행합니다. 식으로 살펴보면

$L(x, g(f(x))) + \Omega(h)$

로 표현할 수 있습니다.

![What happens in Sparse Autoencoder

by Syoya Zhou

Medium](https://miro.medium.com/max/1648/1*k9RX5_kDYt2kG0u9ZREu5w.png)

SAE는 Hidden Layer가 Sparse하도록 지정하기 때문에, 단순히 Input을 Output으로 Copy하는 것보다 더 많은 정보들을 실질적으로 학습할 수 있습니다. 그리고 지속적으로 책에서 Identity Function이라는 말이 나오는데 이는 Copy와 같은 의미라고 생각하시면 됩니다.

Denoising Autoencoders

SAE에서는 Loss Function에 정규화를 적용하였지만 Denoising Autoencoders(DAE)에서는 Loss Function에 적용하는 것이 아니라, 애초에 Input에 Noise를 추가합니다.

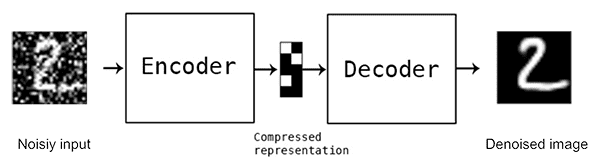
즉, Input $x$를 $\tilde x$로 Noise를 추가하여 오염시킨 뒤, 원래의 $x$를 복원하는 과정을 거치게 됩니다. 이는 단순 Copy보다 많은 정보를 학습할 수 있게 되는 것입니다.

간단한 설명 후에 수식, 확률 분포로 DAE를 나타내보겠습니다.

$C(\tilde x | x)$는 data sample $x$가 주어졌을 때, Corrupted Sample $\tilde x$의 조건부 분포를 나타냅니다. 이후 Decoder가 $p_{reconstruct}(x|\tilde x)$로 표현하여 재구축 분포를 나타냅니다. 즉,

Training data로부터 $x$를 Sample한다.
$\tilde x$를 $C(\tilde x | x)$로부터 추출

Denoising Autoencoder는 생각해보면, NN을 Denoising에 사용하는 것과 같기에 MLP에서 RNN으로 Denoising을 하는 것과 다르지 않습니다. 하지만 이것을 굳이 이름 지어서 나타내는 이유는 DAE의 목적이 Denoise가 주가 아니기 때문이며, 양질의 Representation을 학습하기 위해서이기 때문입니다.

Regularizing by Penalizing Derivatives

Representational Power, Layer Size and Depth

AE는 보통의 경우 Single Layer Enc / Dec로 훈련되지만, 꼭 그럴 필요는 없습니다. 사실 NN 자체가 Deep Learning으로 발전하는 과정이 Layer를 많이 쌓은 것인데 굳이 적게 층을 구성할 필요는 없지요.

Deep Learning의 Layer 개수에 대하여 언급할 때마다 등장하는 개념이 있습니다.

Universal Approximator Theorem: 최소 하나의 Hidden Layer가 있다면, 적당한 Hidden Unit이 있을 때 적당한 Accuracy를 달성할 수 있다.

따라서, 하나의 Layer가 Copy의 역할을 충분히 해낼 수 있으니, 더 쌓으면 더 좋은 성능을 나타낼 수 있다는 것입니다. 그런데 Layer가 하나이면 Input에서 $h$까지의 깊이가 얕으므로 Constraint를 적용하기에는 공간이 부족하기에 Deep Autoencoder를 통해 보완할 수 있습니다.

또한 Depth가 깊다면 Computational cost를 급감시킬 수 있으며, 학습을 위한 데이터 개수도 줄여낼 수 있습니다. 사실 실험적으로 봤을 때, Deep AE가 Shallow나 Linear한 AE보다 성능이 좋다고 합니다.

Learning Manifolds with Autoencoders

Manifold의 특징:

모든 AE는 다음의 두 힘의 절충 또는 Trade-off로 나타납니다.

$x$는 다시 $x$로 복원할 수 있는 $h$를 찾는다. $x$가 training data에서 추출되었다는 사실이 은근히 중요한데, AE가 Data-generating distribution 내에 포함되지 않은 데이터를 굳이 생성해낼 필요가 없기 때문이다.
정규화 Term을 만족한다. 이로써 Input에 덜 민감한 모델을 구축할 수 있다.

Contractive Autoencoders

Contractive의 단어 자체는 ‘수축’이라는 뜻을 가집니다. 즉, $h$의 개수를 줄여버리는 SAE와 다르게 CAE는 $f$의 미분값을 최대한 작게 만드는 것이 목적입니다. 이 때 미분의 대상은 Encoder / Decoder 중 Encoder에 해당하며, Jacobian Matrix의 Squared Frobenius Norm, 좀 더 편한 표현이 Euclidean Norm입니다.

DAE와 CAE는 연관성이 강하게 나타납니다.

DAE의 Reconstruction Error는 CAE의

이 파트가 좀…

CAE를 통해 저차원 Manifold를 구성

Training Set에 포함되어 있는 데이터에 대해서만 Feature를 추출하고 싶기에, Manifold에 대한 이야기로 넘어가는거 아닌가 싶다.

Training Data에 대해서는 Variant하나, 다른 종류의 데이터들에 대해서는 Invariant한 Robust한 모델을 구성하고자 하는 것이 목표이다.