Algorithm: Graph

이번 포스트에서는 알고리즘의 그래프 문제를 어떻게 접근해야 할지에 대한 내용입니다. 저의 개인적인 생각으로는 그래프 문제를 제대로 풀 줄 알아야 알고리즘 실력의 한 단계를 끌어올릴 수 있다고 생각하는데 그 이유는 아래와 같습니다.

Simulation에 대한 연습
약간 난이도가 올라가면 DP / Greedy Algorithm과의 결합이 높다.

알고리즘 애송이이므로 거두절미하고 바로 본 포스팅 진행해보겠습니다.

Graph

먼저 그래프 문제의 접근법에 대하여 나열을 해보겠습니다.

1. 그래프 구성

그래프를 구성하는 방법은 크게 두 가지로 생각되며, Dictionary와 Array로 구성하는 것입니다. 알고리즘 테스트를 공부하기 위한 도서 중 호평을 많이 받은 ‘파이썬 알고리즘 인터뷰’에서는 Dictionary를 구성하는 방식을 먼저 소개합니다.
따라서 저는 해당 방식이 가장 공식적인 형태인 줄 알았지만 문제를 풀다보면 Array를 통한 구성이 가장 많이 사용되는 듯 하였으며, Grid를 구성하여 문제를 접근하는 풀이가 많았기에 밑에서 설명할 문제들도 Grid를 사용할 것입니다.

# Dictionary로 구성한 그래프는 각 노드에 어떤 노드들이 연결되어 있는지 Key와 Value로 구성
dictionary_graph = {
  1: [2,3,4],
  2: [5],
  3: [5],
  4: [],
  5: [2,4],
  6: [],
  7: [3]
}

# Array로 구성한 그래프는 배열 안에 연결된 노드를 표시. 1번째 리스트는 2,3번 노드와 연결이 되어 있으며, 0번째는 Padding으로 추가한 것이다. 문제에 따라 인덱스가 1부터 시작하는 경우가 있기에 유용.
grid_graph = [[0, 0, 0, 0, 0, 0],
              [0, 0, 1, 1, 0, 0],
              [0, 1, 0, 0, 0, 1],
              [0, 1, 0, 0, 1, 0],
              [0, 0, 0, 1, 0, 1],
              [0, 0, 1, 0, 1, 0]]

2. DFS / BFS

그래프를 구성한 뒤에는 각 노드를 Traverse (순회) 하면서 원하는 목적을 위해 탐색합니다. 이런 탐색이 그래프 문제의 본질이며 (아직까지 많은 문제를 풀어보지 못한 애송이의 관점), 탐색이 본 목적은 아니지만 탐색 알고리즘을 통해 목적을 달성합니다.

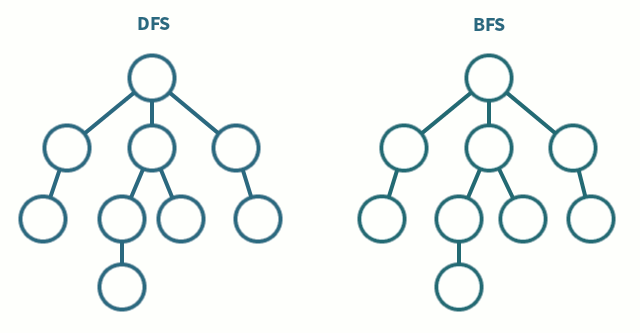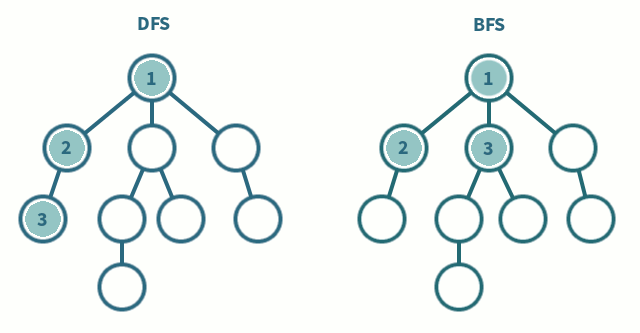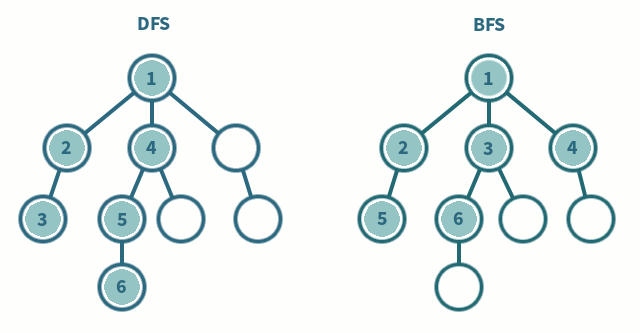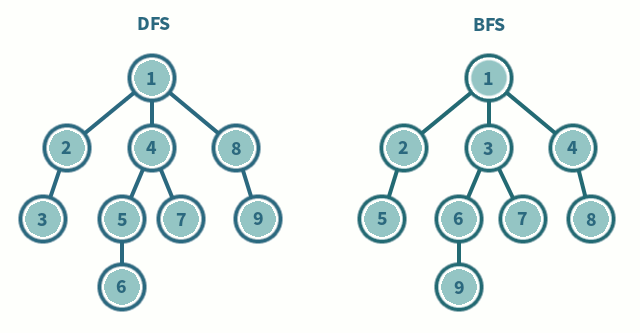
저는 개인적으로 공부나 암기를 할 때, 모든 것을 다 외우지 못하기 때문에 한마디로 요약해서 무엇인지 파악하려 합니다. 따라서 DFS, BFS 역시 제가 느낀 인상들을 간략하게 나타내보고자 합니다.

DFS DFS는 Depth-First Search의 준말로 그래프를 탐색함에 있어 무조건 깊게 내려가는 것을 먼저 진행합니다.
DFS는 하루의 계획을 잡을 때 있어 전체 큰 그림을 보지 못하고 Greedy Algorithm 마냥 눈 앞에 보이는 Task만을 진행합니다. 즉, Disgusting 하죠. 저 또한 그러지만 자신이 할 일을 계획에 따라 차근차근 하지 않으면 보통 하루의 계획이 망하드라구요…
DFS는 마구잡이, 무계획성이 있는 녀석이라고 보시면 되며 Stack 또는 재귀 (쟤는 자기 시간만 귀하다 -> 재귀)를 통해 문제를 풉니다.

BFS BFS는 Breadth First Search의 준말로 그래프를 탐색함에 있어 깊게 내려가는 것이 아닌 자신이 인접한 노드들을 먼저 모두 탐색하는 것을 말합니다. DFS와 다르게 BFS는 큰 그림을 그리는 밥 아저씨 알고리즘으로서 아무리 해야할 일이 갑작스레 등장한다고 해도, 자신이 계획했던 것에서 벗어난다면 후순위로 미뤄두고 먼저 약속한 일들을 행합니다. 즉, Best 한 녀석입니다.
BFS는 Queue를 구성해서 만들어야 하며 재귀를 사용하면 안됩니다. 또한 Queue를 만들 때는 List를 통해 구성하여 풀어도 되지만 collections.deque를 사용하지 않으면 효율성이 떨어져 에러가 나타난다는 소식을 접했기에 이를 사용하는 것을 습관화 들여야 합니다.

from collections import deque

queue = deque()
queue.append(node)
node = queue.popleft()

3. Visited

Graph 문제를 풀기 위해선 Graph를 구성해놓는 것에 더하여 Visited라는 기록장이 필요합니다. Graph의 노드가 1~5가 있고 이를 순서대로 방문한다고 했을 때, 2를 방문한 시점에서 방문을 완료한 노드는 1,2일 것입니다. 이것을 기록해두어야 나중에 다시 그 노드를 방문해도 지나치거나 애초에 방문할 계획을 잡지 않아야 효율적으로 순회를 마칠 수 있습니다.

Graph 문제를 접근하기 위해 필요한 요소를 정리해보자면

그래프 문제는 그래프가 필요
어떻게 탐색할지 결정: BFS / DFS
기록장 구성: Visited

백준 알고리즘에서 가장 기본적인 그래프 문제는

1260: DFS와 BFS

입니다. 이를 풀고 다음 Graph 실전 문제를 풀어나가시다보면 감이 오시지 않을까 싶은데 저도 아직 오지 않았습니다 (에욱).

1260: DFS와 BFS

문제

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

입력

첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

출력

첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.

# 입력 처리
N, M, V = map(int, input().split())
graph = [[0] * (N+1) for _ in range(N+1)]

# 구성한 Graph에 연결 여부 삽입
for _ in range(M):
    a,b = map(int, input().split())
    graph[a][b] = graph[b][a] = 1

# BFS는 무조건 deque! (아닌 경우를 마주해보고 싶다.)
from collections import deque

dfs_answer = []
visited = [0] * (N+1)

# DFS: Recursive Version
# 1. V: 시작 노드, N: 정점 개수 
# 2. 방문한 노드를 정답에 포함하고, Visited에 기록 (Visited[V]=1)
# 3. (1, len(graph[V]))는 (1,Node 개수)이며, 하나의 노드에 대해 자신의 이웃을 탐색
# 4. 이때, 재귀를 사용했으므로 연쇄적으로 이웃 탐색을 진행한다.

def dfs(V, N):
    dfs_answer.append(V)
    visited[V] = 1
    for i in range(1, len(graph[V])):
        if graph[V][i] and not visited[i]:
            dfs(i, N)
            
# BFS: Deque-queue   
# 1. V: 시작 노드, N: 정점 개수 
# 2. deque를 통해 queue를 만들고 시작 노드 추가하며, Visited에 기록
# 3. Queue에 노드가 없어질 때까지 반복하며, queue의 앞쪽에서 노드를 하나씩 빼서 처리
# 4. 1번 노드가 2,3,4와 연결이 되어 있으면, 1번 노드 visited 처리 후 연결 되어 있는 2,3,4 노드에 대해 queue에 얹고 visited에 기록.
# 5. queue에 2,3,4가 들어가있지만 visited에 기록이 되어있으니 queue에 다시 들어가지는 않으며, 노드 2 차례때 그에 연결되어 있는 노드들을 queue 뒤에 삽입하여 후에 처리될 수 있도록 설정
 
def bfs(v, N):
    visited = [0] * (N+1)
    queue = deque()
    queue.append(v)
    answer = [v]
    visited[v] = 1
    
    while queue:
        node = queue.popleft()
        
        for i in range(1, N+1):
            if graph[node][i] == 1 and visited[i] == 0:
                queue.append(i)
                visited[i] = 1
                answer.append(i)
                
    print(' '.join(map(str,answer)))
    
dfs(V, N)
print(' '.join(map(str, dfs_answer)))
bfs(V, N)

1303: 전쟁-전투

해당 문제는 BFS를 통해 푸는 그래프 문제입니다. 그래프 문제가 어려운 이유는 해당 문제를 그래프로 접근해야겠다 라는 생각이 들어도 어떤 탐색기법을 사용해야할 지 판단하기 어려운데 이것은 연습을 통해 해결되길 바랍니다 (저도 잘 모르겠습니다).

전쟁-전투에 대한 설명은…좀 더 그래프 문제를 풀어본 이후 깨달은 바를 함께 포함시켜서 작성하도록 하겠습니다.

from collections import deque
import sys

def bfs(x, y, color):
    queue = deque()
    queue.append((x,y))
    visited[x][y] = True
    
    total = 1
    while queue:
        x,y = queue.popleft()
        for index in range(4):
            x_axis = x + dx[index]
            y_axis = y + dy[index]
            if 0 <= x_axis < m and 0 <= y_axis < n:
                if graph[x_axis][y_axis] == color and not visited[x_axis][y_axis]:
                    visited[x_axis][y_axis] = True
                    queue.append((x_axis,y_axis))
                    total += 1
    return total

n, m = map(int, input().split())
graph = [list(input()) for _ in range(m)]
visited = [[False] * n for _ in range(m)]

dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]

white, blue = 0,0
for i in range(m):
    for j in range(n):
        if graph[i][j] == 'W' and not visited[i][j]:
            white += bfs(i,j,'W')**2
            
        elif graph[i][j] == 'B' and not visited[i][j]:
            blue += bfs(i,j,'B')**2
            
print(white, blue)

취업을 위해 열심히 노력하겠습니다. 오늘도…
이상 전달 끝!