GNN Explainer: Generating Explanations for Graph Neural Networks

Introduction

GNN의 장점에 대해서 논할 때 항상 등장하는 말이 ‘관계성’입니다. Non-relational Data, 즉 우리가 일반적으로 살펴볼 수 있는 DataFrame 꼴의 데이터는 각 데이터들이 Independent하다는 가정을 갖고 있는데, 이는 Social Network, Chemical Data 등과 같이 관계가 중요한 요소로 자리매김 하는 Relation Data과 차이가 있으며 이에 대해선 해당 관계성을 반영할 수 있는 기법을 사용해서 분석해야 합니다. GNN이 바로 이 관계성을 담을 수 있는 기법이므로, 얽히고 설킴이 강한 현대 사회의 네트워크를 분석하기에 최적의 기법인 것입니다.

Adjacency Matrix

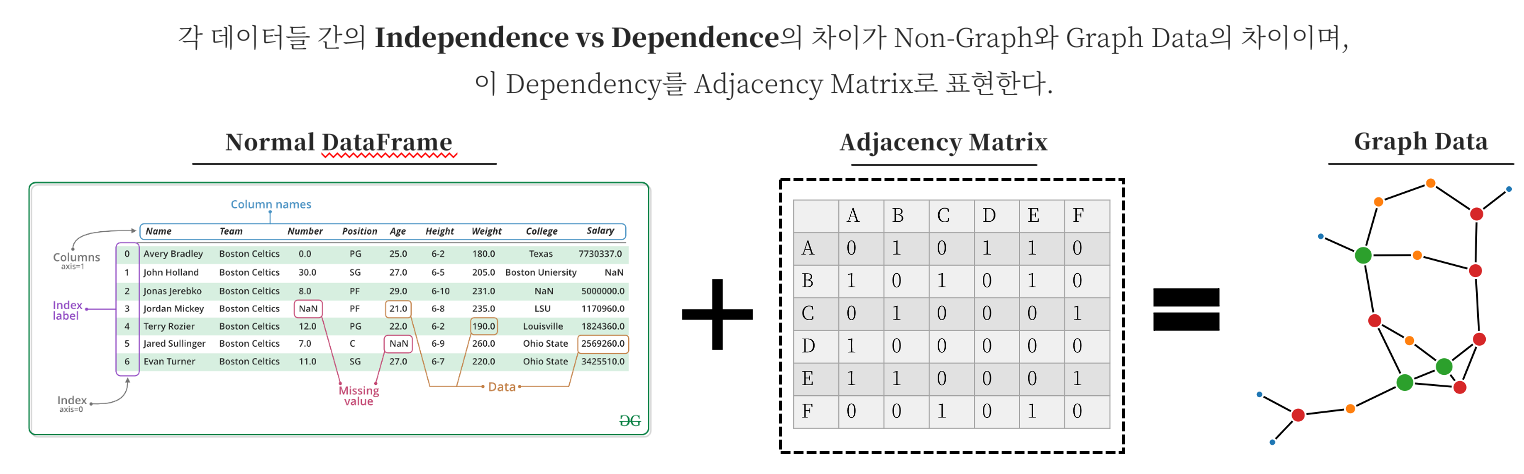
GNN이 관계성을 정의하는 방식은 대표적으로 Adjacency Matrix입니다. Laplacian, Degree Matrix 등과 같이 다른 행렬들도 존재하지만, 실질적으로 보면 Adjacency가 다른 형태의 행렬들의 근간을 이룹니다. Adjacency Matrix를 통해 하나의 노드 주위에 어떤 노드들이 존재하는 지, 즉 이웃을 파악할 수 있고 Graph 전체의 구조도 파악할 수 있게 됩니다.

Graph Neural Network XAI

위와 같은 방식의 GNN은 일반적인 Neural Network보다 성능이 크게 상승하지만, 그 복잡성 역시 상승하여 Black Box로 치부되던 딥러닝이 더 어두워지는 느낌이 있습니다. 따라서 Explainability를 달성하기가 어렵지만 이를 달성해야만 하는 이유는

• GNN Model에 대한 신뢰성 / 투명성 향상
• Network 특징을 파악함으로써 모델에 존재할 수 있는 Error를 파악

이 가능하기 때문입니다.

Graph의 Explainability를 다룬 논문은 신기하게도 이전에는 하나도 존재하지 않아, 본 논문이 최초라고 할 수 있으며 비슷한 시기에,

Explainability Methods for Graph Convolutional Neural Networks (Phillip E. Pope et al / CVPR, 2019)

가 나오긴 했지만 간발의 차로 더 빠릅니다. 또한 해당 논문은 GCNN 계열의 기법들에만 적용할 수 있는 방법으로서, 기존의 CNN이 Saliency Map을 구성하기 위해 존재하던 기법을 그대로 가져다 사용한 것이지만 GNNExplainer는 최적화 방식으로 진행합니다. 이 최적화 방식에는 Variational Inference / Monte Carlo Estimate과 같이, 뭔가 많이 들어봤지만 파고들기 겁나는 개념들이 많이 존재하여, GNN Explainer와 같이 친숙한 이름을 갖고 있어도 내부의 사정은 매우 복잡합니다.

Explainability in Graph Neural Networks: A Taxonomic Survey (Yuan et al. 2020)

위의 Survey 논문에서는 GNN에 적용되는 XAI를 정리해놓았는데 해당 논문에서 XAI 종류를 분류해놓은 그림이 있어서 소개합니다.

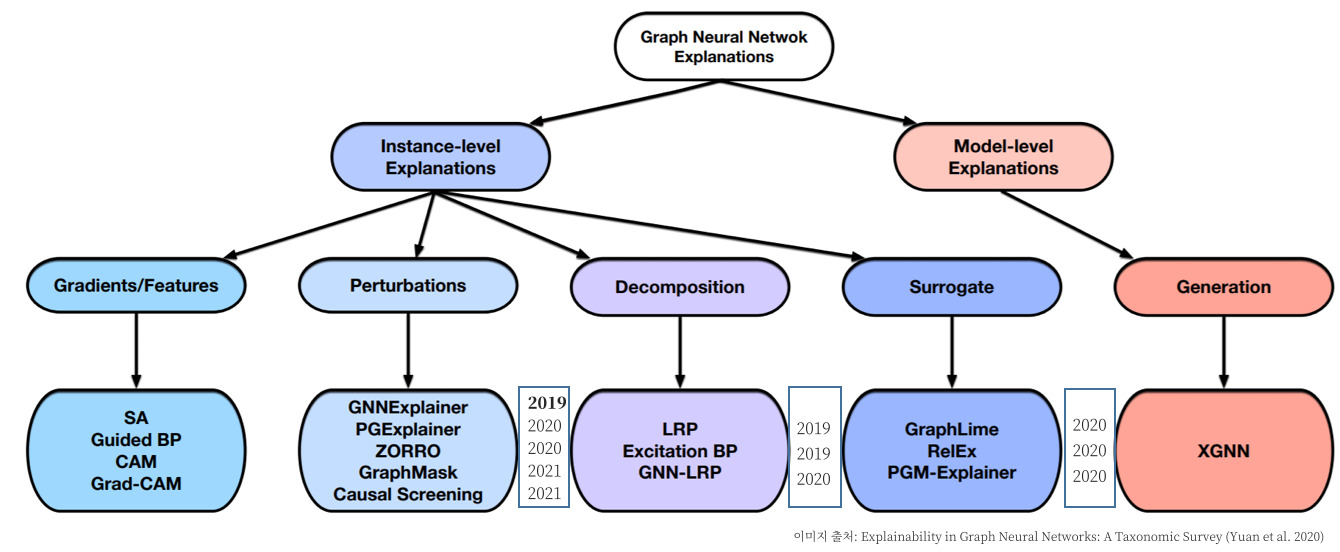
확실히 Perturbations 항목에 포함되어 있는 GNN Explainer가 2019년으로 가장 빠르고 다른 기법들이 2020년에 모두 나타난 것으로 보아, GNNExplainer가 GNN XAI의 횃불을 지폈다고 할 수 있습니다. 다른 Decomposition / Surrogate 류의 기법도 살펴보고 싶지만, 본 포스트에서는 Perturbation류의 대표주자인 GNNExplainer를 살펴보겠습니다.

그럼 여기서 XAI에 대해서 알고 계신 분들이라면 의문이 드실 수 있습니다.

기존의 Model Agnostic Approach 인 LIME / SHAP을 사용하면 되지 않나?

하지만 두 기법들은 위에서 설명한 Independence한 데이터를 설명하기 위한 기법들이며, 관계성이 반영되어 있는 데이터, 그리고 Adjacency Matrix도 데이터 범위에 포함되어 있는 Graph 데이터에는 적용하기 힘듭니다. 또한 Graph Data의 Explanation은 두 가지로 나타나는데, 먼저 통상적으로 진행되어온

• 어떤 Feature가 Prediction에 큰 영향을 주었는가?

이 진행되기도 하지만, 사실 더 중요한 그리고 본 목적은

• 어떤 노드가 중심 노드의 Embedding 형성에 더 큰 영향을 주었는가?

에 대한 답을 구하기 위해서입니다.

위의 그림으로 GNN XAI에 대한 Overview를 살펴볼 수 있는데, 먼저 Input Graph의 하나의 노드 Embedding을 도출해내고 그것에 대한 Classification을 하는 모델이 있다면, 해당 노드를 특정 Class로 분류함에 있어 영향을 미친 노드들, 즉 Subgraph를 찾는 것이 GNN XAI의 목적입니다.

Related works

Explainability 기법 종류

GNN의 Explainability를 다룬 선례가 없기 때문에 기존 ML / DL에서 사용했던 방식을 정리하자면 몇 가지 방식으로 나뉩니다.

• Surrogate / Proxy Model을 구성한 뒤, Explanation을 찾는다.
• High level feature를 설명할 수 있는 연관 변수를 찾는다.
• Computation 과정에 지대한 영향을 주는 주요한 변수를 찾는다. $\Rightarrow$ Feature Gradients, Backpropagation, Counterfactual reasoning 이런 기법들로 생성한 Saliency Map은 잘못된 결과를 낳을 수 있고, Gradient Saturation과 같은 문제를 겪을 수 있는데, 특히 Adjacency Matrix에서 문제가 증폭될 수 있기에 GNN에 사용하기에는 부적합한 기법이다.

하지만 이런 기법들은 Graph의 정수라고 할 수 있는 관계성을 포함하지 못하기 때문에, Node Feature와 관계 정보를 모두 담을 수 있는 기법이 필요하게 됩니다.

GNNExplainer

GNN Explainer를 GNN의 Prediction을 설명하기 위한 기법으로서, 훈련된 GNN과 Prediction을 가지고 특정 노드나 Class에 대하여 Subgraph를 구성하며, 이를 통해 어떤 노드가 하나의 노드 또는 Class를 구성하는데 영향을 주었는지 알 수 있습니다. 또한 영향 노드만을 구할 수 있는 것이 아니라, 노드의 어떤 Feature의 영향력이 큰지에 대해서도 알 수가 있어 더 심화적인 분석이 가능합니다. 정리하자면

• 하나의 노드를 구성함에 있어 어떤 이웃의 노드들이 영향을 미쳤는지 (Single-instance explanations)
• 하나의 Label을 갖는 노드들에 대하여, 어떤 이웃의 노드들이 영향을 미쳤는지 (Multi-instance explanations)
• 노드 내의 어떤 Feature가 영향을 미쳤는지

로 나누어볼 수 있습니다.

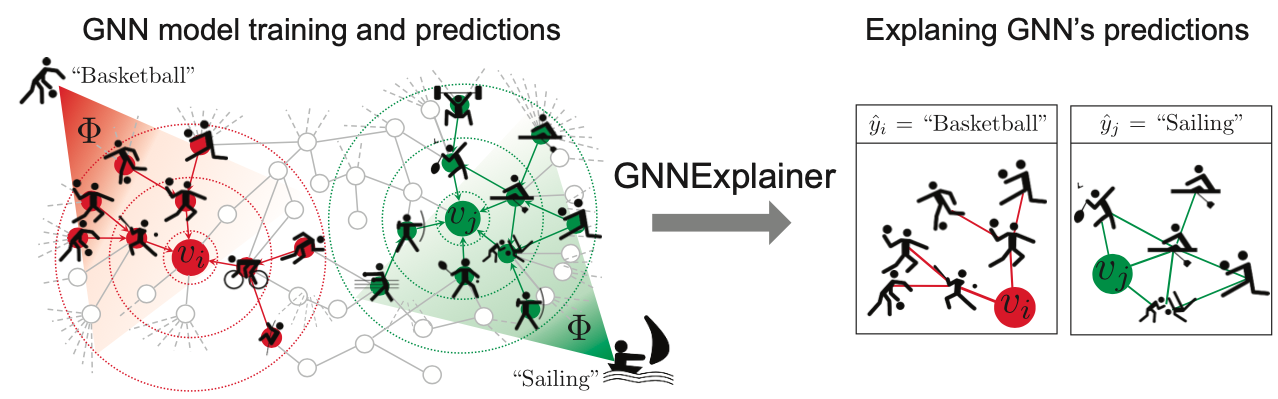
위의 그래프를 예시로 살펴보겠습니다. 각 노드는 학생들이며, Label은 취미 운동을 어떤 것을 갖고 있는지에 대한 그래프를 나타내고 있습니다. $\Phi$를 Node Classifcation을 진행하는 GNN Model이라고 했을 때, $v_i, v_j$ 노드가 어떤 운동을 선택할 지 판단하는 문제라고 할 수 있는데, 빨간색의 모델이 $v_i$를 농구라고 분류하고 초록색의 모델이 $v_j$를 Sailing이라고 분류하는 경우입니다. 훈련된 모델과 Prediction이 존재할 때 GNNExplainer는 각 노드가 판단을 하기 위한 요소들이 무엇인지 판단하여 우측의 그림처럼 Subgraph를 나타낸 것을 볼 수 있습니다. 빨간색 모델과 농구로 분류한 경우를 살펴보면 $v_i$노드는 자전거, 달리기와도 연결이 되어있지만 ‘공과 관련된’ 운동들이 더 주요한 영향을 끼쳤기에 농구라고 분류했다고 할 수 있습니다.

이를 달성하기 위하여 GNN Explainer는 GNN의 Prediction과 Mutual Information을 최대화 하는 Subgraph를 탐색합니다. 해당 Optimization을 설명하기 위하여 Single Instance Optimization부터 설명드리겠습니다.

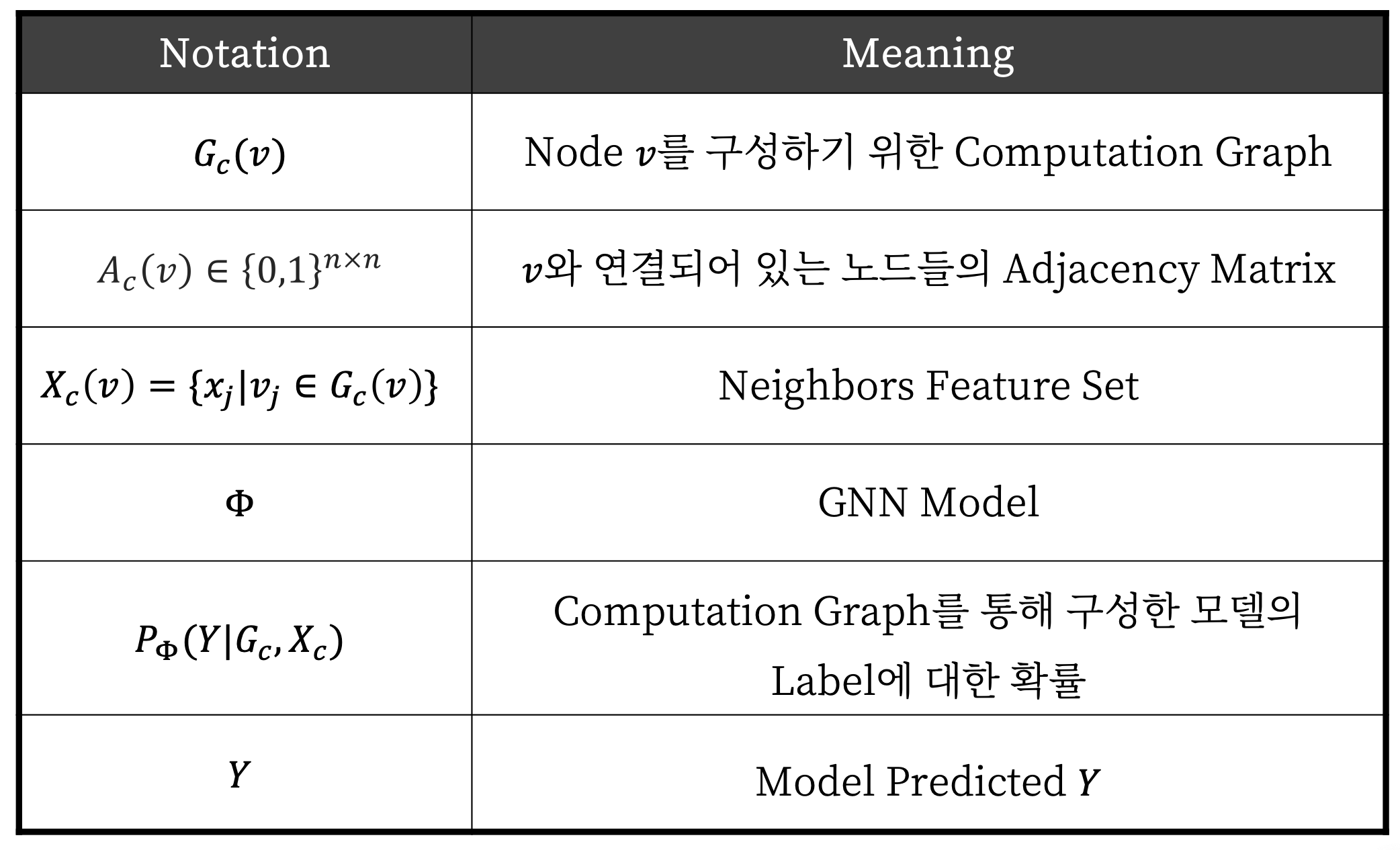
GNNExplainer: Notation

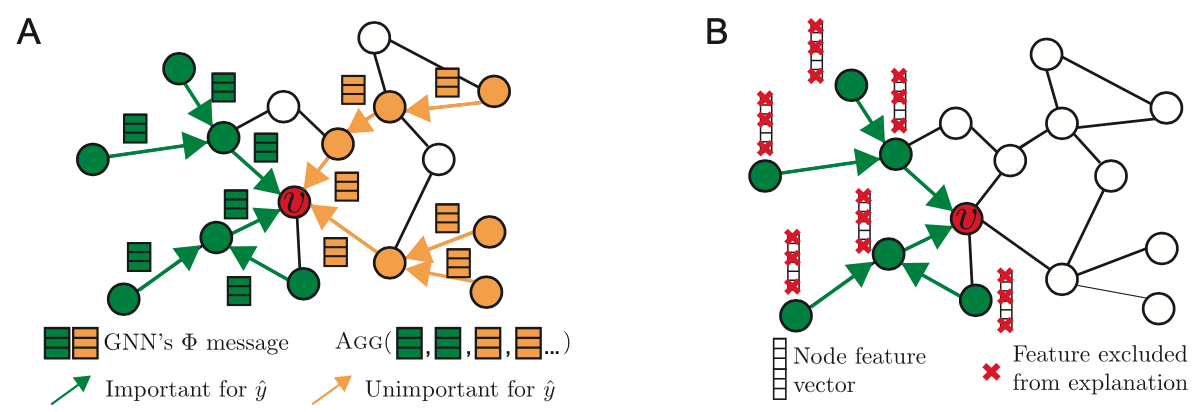
GNN 기법으로 Node $v$의 Embedding $z$를 판단하고자 합니다.

• $G_c(v)$: $v$를 $z$ Embedding으로 구성하는 Computation Graph. Computation Graph는 계산 과정을 위해 필요한 노드들을 엮은 그래프를 뜻한다. 위의 그림 A에서 색깔로 표시된 그래프들이 Computation Graph이며, 초록색은 $\hat y$를 구성할 때 중요한 노드들이며, 노란색은 반대의 의미이다.
• $A_c(v) \in {0,1}^{n \times n}$: Adjacency Matrix는 0과 1사이의 값으로 $n \times n$ 차원으로 이루어져 있다.
• $X_c(v) = {x_j|v_j \in G_c(v)}$: $v$를 구성하기 위한 Computation Graph내에 있는 노드들의 Feature들이다.
• $P_{\Phi}(Y|G_c, X_c)$: 노드들의 Feature들과 Computation Graph를 사용했을 때 {1, …, C} 종류의 Label을 가질 확률을 표현한 것이다.

여기까지가 기존 모델에 대한 Notation 입니다. 위의 Notation을 통해 모델을 구성하고 그에 따른 결과들의 확률을 표현할 수 있습니다. 이 중, GNNExplainer는 일부의 Subgraph와 일부의 Sub-Feature를 Masking을 통해 얻어내고자 합니다.

• $G_S$: Computation Graph $G_c(v)$의 Subgraph

• $X_S$: $G_S$에 포함되어 있는 Feature

• $X_S^F$: $X_S$ 중 일부의 Features / 위의 그림 B에서 빨간색 x로 삭제되지 않은 Features이다.

  

Single Instance Optimization

최적화를 위하여 단일 노드 $v$에 대하여, Computation Graph $G_c$ 내에 포함되어 있는 Subgraph $G_S$ 중, Mutual Information이 가장 큰 $G_S$를 선택합니다. 이 때 예시를 통해 살펴보자면 아래 그림과 같습니다.

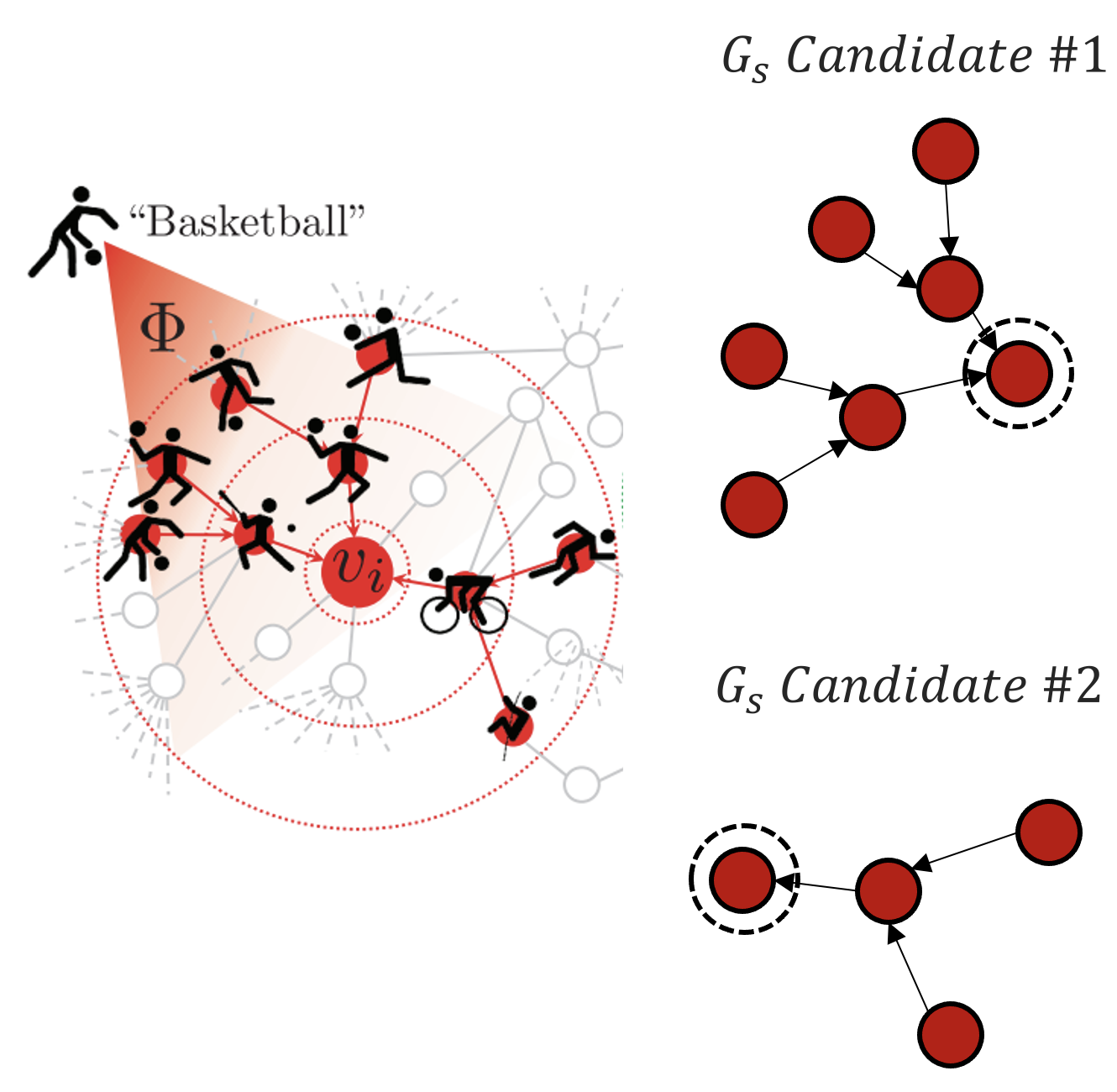
노드 $v_i$ 의 Embedding을 구성하여 Label을 정의하기 위하여 모델에서 사용하는 모든 노드들을 $G_c$ 라고 했을 때, 전부를 활용하는 것도 가능하지만, 그 중 필요한 노드와 불필요한 노드가 존재할 것이며, 불필요한 노드는 최악의 경우 더 나은 결과를 얻는 것을 저해할 수 있습니다. 따라서 핵심적인 노드만을 판단하기 위해 $G_c$ 내에 존재하는 여러 경우의 $G_S$ 를 구해 그 중 Mutual Information이 최대인 $G_S$를 구하는 것입니다. 위의 그림에서 $G_c$에서 $G_S$ 후보들을 나타내는 것을 볼 수 있습니다.

이 때, Mutual Information(MI)에 대한 식은 아래와 같이 표현할 수 있습니다.

$max_{G_S} MI(Y, (G_S, X_S)) = H(Y) - H(Y|G=G_S, X = X_S)$

MI에 대한 일반적인 정의는 두 변수의 상호 종속 여부라고 할 수 있는데, 두 변수가 독립이라고 했을 때와 종속이라고 생각했을 때의 두 변수의 결합확률의 차이로서, 이 값이 크게 되면 두 변수가 독립이 아니라 종속에 가까우므로 관계가 크다고 할 수 있습니다. 즉, 위의 식에서는 $v_i$ 의 예측값인 $Y$ 와 Subgraph $G_S, X_S$ 의 연관성이 크다고 할 수 있는 것입니다.

MI의 최적화 식에서 $H(Y)$ 는 모델에서 모든 Computation Graph를 사용했을 때의 Return 값에 대한 Entropy이므로 고정입니다. 따라서 해당 최적화 식을 우항의 $H(Y|G=G_S, X = X_S)$ 를 최소화 시키는 것으로 전환할 수 있게 됩니다.

$min H(Y|G=G_S, X = X_S)$

해당 식은 Subgraph $G_S$의 Entropy인데, 본디 Entropy란 불확실성을 의미하기에 이를 최소화 한다는 뜻은 모델 $\Phi$의 불확실성을 줄인다는 뜻이 됩니다. 따라서 최적화 식의 의미가 목적과 결부하게 되며 이 때, $G_S$ 의 크기를 $K_M$ 으로 한정시켜 적당한 크기로 유지하기 됩니다.

그런데 아쉽게도 해당 최적화 식은 직접적으로 사용할 수 없습니다. 그 이유는 $G_c$내의 수 많은 $G_S$가 존재하며 이들에 대하여 모두 비교하여 최적의 $G_S$를 판단하는 것을 불가능하기 때문입니다. 하나의 $G_c$가 M개의 노드를 갖고 있다면, 포함되어 있는 $G_S$ 의 개수는 $2^M$개입니다.

수많은 $G_S$는 Intractable하므로 이를 해결하기 위해, $G_S$ 에 대하여 근사를 진행하며 이는 Random Graph를 Variational Distribution으로 정의하는 Variational Inference를 포함하고 있습니다. 또한 $G_S$들을 분포로 나타내기 위하여 Continuous Relaxation을 진행하며, Adjacency에 포함되어 있는 각 Cell을 0~1사이의 확률값으로 나타냅니다. 이에 따라 식을 변경하게 되면,

$min_\mathcal G E_{G_S\sim \mathcal G}H(Y|G = G_S, X = X_S)$

그리고 이를 Jensen’s Inequality로 Upper Bound로 전환하면,

$min_\mathcal G H(Y|G = E_\mathcal G[G_S], X = X_S)$

로 표현할 수 있습니다. 이 Upper bound를 Minimize하는 것이 원래의 식을 Minimize하는 것과 같은 맥락을 갖게 됩니다.

따라서 이제 $E_\mathcal G[G_S]$를 도출해내야 하므로, $G_S$를 계산하기 위하여 Mean Field Variational Approximation을 사용합니다. 특히 Mean Field를 사용하는 이유는 기대값을 구하기 편한 방법이기 때문이며, 개념이 어려울 수 있으나 단순히 결합분포를 구하기 위하여 Marginal Distribution을 모두 독립으로 간주하고 곱했다고 생각하시면 편합니다. 따라서 아래의 그림처럼 $G_S$를 구할 수가 있는데, 이렇게 연속적으로 Adjacency Matrix를 곱하는 과정을 오른쪽의 Masking과정으로 변환합니다. 논문에서 이렇게 변환하는 원리에 대한 특별한 설명이 없지만 제 생각에는 $G_S$의 Cell에 포함되어 있는 확률값이 계속 작은 값이 곱해질수록 0에 수렴하게 되므로, Masking의 효과가 있다고 간주하는 것 같습니다.

(확률 분포의 기대값을 구하는 과정이 왜 Masking과 연관이 되는지 몰랐으나, 이를 일깨워준 김명섭 석박 통합과정에게 감사의 인사를 올립니다.)

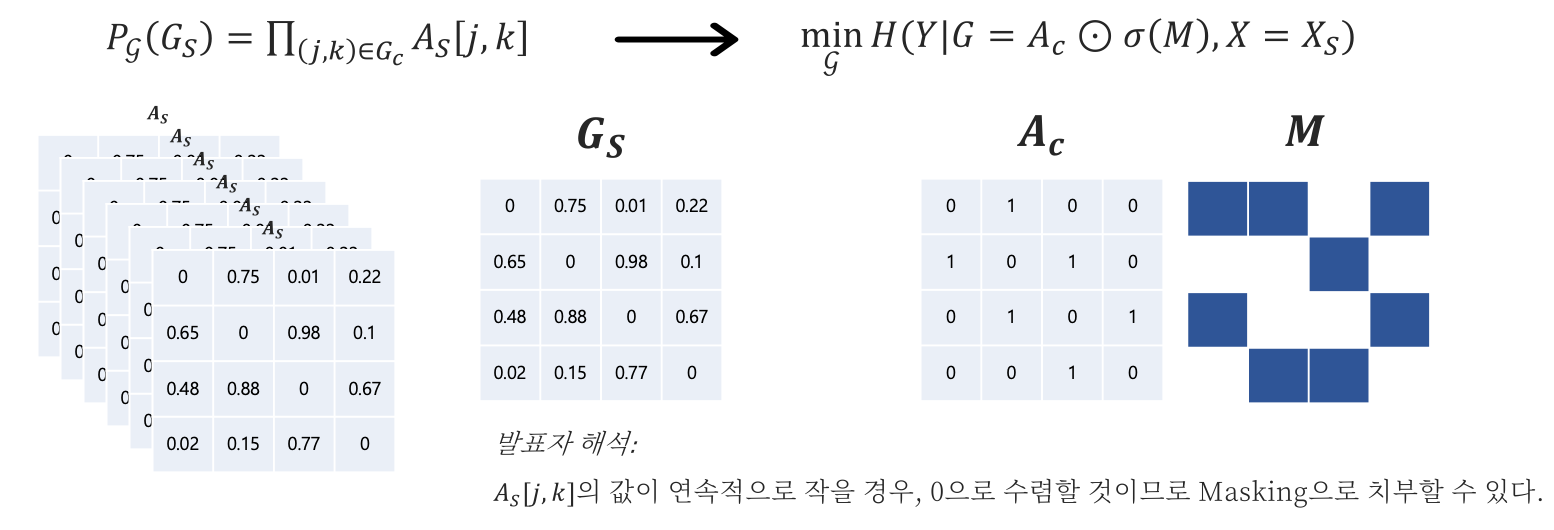
따라서 지금까지 Mutual Information을 최대화 하기 위하여, Masking을 사용하는 식으로 변환하여 최적화를 진행한다는 것을 유도해 나갔습니다.

Why Variational Inference?

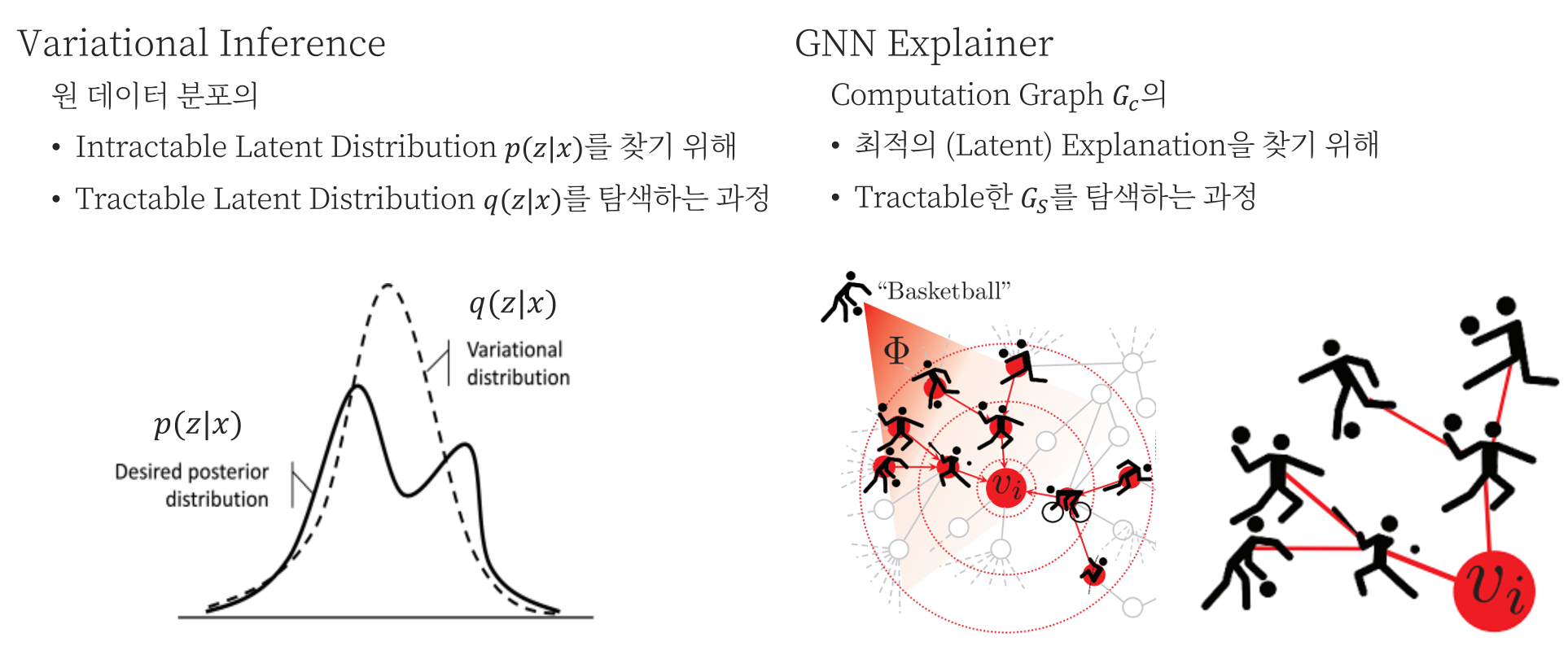
살짝 짚고 넘어가고 싶은 부분은 GNN Explainer를 형성하는데에 있어, 왜 Variational Inference를 사용했는가 입니다. Variational Inference를 사용하는 경우는 Latent를 표현하는 Posterior 분포 $p(z|x)$가 Intractable할 때, Variational Distribution $q(z|x)$를 사용하여 근사하는 과정입니다. 즉, 분포의 Latent를 파악하는 것에 목적이 있는데, 이를 GNN Explainer에 연관짓자면, $G_c$ 속에 있는 Latent, $G_S$ 를 파악하는데에 있습니다.

따라서 전체 $G_c$ 중 중요한 Latent만을 뽑는 과정을 포함시켜야 하기 때문에 Variational Inference가 포함되지 않았을까 추측해봅니다.

Prediction vs Label

다음으로 논문에서 다소 헷갈리는 개념이 있습니다. GNN Explainer는 어떠한 Task를 통해 훈련된 모델에 대한 설명을 하는 모델입니다. 따라서 Input으로 모델이 포함되는 것입니다.그런데 모든 Trained Model은 Prediction과 Label이 존재합니다. 이를 통해 훈련이 진행되었을 것이고, 최대한 Prediction과 Label이 일치하는 방향으로 진행되었을 겁니다. 하지만 훈련이 많이 되었다고 하더라도, 예측값과 정답이 완벽하게 일치하는 경우는 없으며, 오히려 둘이 완벽하게 일치하는 경우는 Overfitting에 가까울 것입니다.

따라서 Single Instance Explanations에서도 분화가 생기게 됩니다.

• Model Prediction vs Masked Prediction

  $min_{\mathcal G}H(Y|G = A_c \odot \sigma(M), X = X_S)$

  “모델이 특정 Prediction으로 예측한 이유가 무엇인가?”

• Model Label vs Masked Prediction

  $min_M - \sum_{c=1}^C 1[y=c]log p_\Phi(Y = y|G = A_c \odot \sigma(M), X = X_c)$

  “모델이 특정 Label로 예측한 이유가 무엇인가?”

이 둘은 비슷해보이지만, 전자는 Model의 Confidence 관점에서 생성한 질문, 그리고 모델의 예측값을 매우 신용하는 경우에 사용하는 것이며 후자는 Label과의 직접적인 비교를 진행할 때 사용됩니다.

Learning Binary Feature Selector $F$

$\hat{y}$에 대하여 어떤 노드 Feature가 지대한 영향을 끼쳤는지 살펴보기 위하여, GNNExplainer는 Feature Selector $F$를 학습하는데, 이는 기본적으로 Graph Structure를 담당하는 Adjacency에 적용했던 방식대로 Masking을 진행합니다. 위에서 $X_S$, 즉 $G_S$에 포함된 모든 Feature들을 사용했다면 지금부터는 이것에 Mask를 얹어서 $X_S^F$를 생성하는 것입니다. 그리고 이 Mask는 Binary로 구성됩니다. 따라서 Mutual Information 관점으로 최적화 식을 다시 구성하자면,

$max_{G_S, F} MI(Y, (G_S, F)) = H(Y) - H(Y|G = G_S, X = X_S^F)$

로 표현할 수 있습니다.

Intergrating additional constraints into explanations

GNNExplainer를 좀 더 좋은 모델로 구성하기 위해 정규화 항을 포함시키는 것도 가능합니다. 예를 들어,

• Mask에 Element-wise entropy를 적용하거나,
• Lagrange Multiplier와 같은 Domain-specific한 제약식을 적용하는 등의 정규화를 적용할 수 있습니다.

논문에서 여러가지를 더 소개하기는 하지만, 매우 추상적으로만 적어놨기에 코드에서 구현이 되어 있는지 아닌지 살펴볼 필요가 있을 것 같습니다.

Experiments

XAI류의 모델들에서 성능 평가는 생소합니다. 과연 각 모델들은 어떻게 성능을 평가하여 이전 기법들과의 비교를 통해 자신들의 기법의 우수성을 자랑할 수 있을까요? Accuracy를 기반으로 하는 것 같지만, 예측 값이 위에서 쭉 설명해온 Subgraph나 Feature라고 했을 때 Label이 무엇인지 잘 모르겠습니다. 따라서 실험 섹션을 보면서 사용하는 데이터 셋과 실험 방법을 살펴보겠습니다. 보통 실험은 저자들의 자랑 시간이라고 생각하여 주의 깊게 살펴보지는 않았지만 요즘 들어 Experiments를 잘 읽어야 논문 전체가 이해 가능한 경우가 많다고 생각이 듭니다.

Datasets

Synthetic datasets

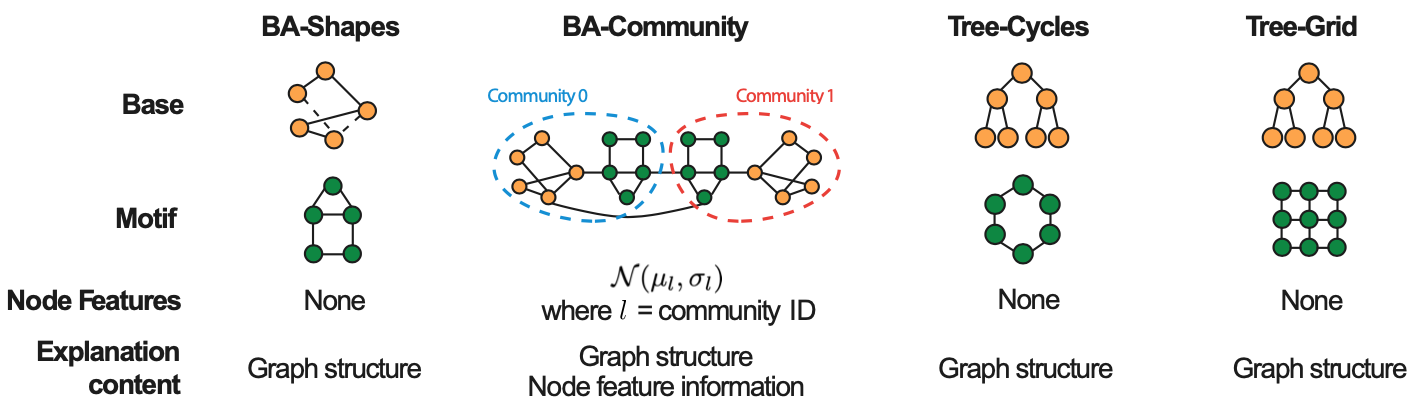
• BA-Shapes
  • 300개의 노드를 가진 Barabasi-Albert(BA) Graph에서 80개의, 5개 노드로 구성된 House 꼴의 Motif를 Random으로 연결한다.
  • 0.1N (N = Node 개수)개의 Edge를 추가적으로 포함해 Perturbation
  • 그래프 내 각 노드들은 4개의 Class가 존재: House의 머리/ 가슴 / 배, House에 포함되지 않는 노드
• BA-Community
  • 2개의 BA-Shapes의 합집합이며, Community와 Role에 따라 8개의 Class로 나누어진다.
• Tree-Cycles
  • 8층의 Tree를 구성한 뒤에 80개의, 6개 노드로 이루어진 Cycle을 가져다 붙힌다.
• Tree-Grid
  • 8층의 Tree를 구성한 뒤에 80개의, 9개 노드로 이루어진 (3x3) Grid를 붙힌다.
  • Tree 계열의 경우, 코드를 살펴보면 Label이 Tree에 속한 노드와 Motif에 속한 경우로 나누어져 있습니다. 즉, BA처럼 노드의 위치에 따른 Label이 아닌 것이다.

Real-World Datasets

• MUTAG
  • 4,337개의 분자 그래프이며, 해당 분자들이 Gram-Negative Bacterium S.typhimurium으로 인한 유전적 변화로 Labeled
  • Label은 1 / -1로 나타나있다.
• REDDIT-BINARY
  • 2,000개의 그래프는 각 Discussion Thread를 나타낸다.
  • Node: User In Thread / Edge: 하나의 유저가 다른 유저에 답장했을 경우
  • Graph는 Thread내에 어떤 User Interaction이 이루어져 있는지 판단한다.
    • Question-Answer Interaction: $r/IAmA, r/AskReddit$
    • Online-Discussion Interactions: $r/TrollXChromosomes, r/athesim$

Alternative Baseline Approaches

GNN Explainer와 다르게 기존의 기법들은 Graph에 직접적으로 적용하지 못합니다. 하지만 비교 군을 수립하기 위하여 몇가지 기법들로 논문에서는 비교를 하나 구체적인 방법에 대해서는 기술하지 않아 구현 코드를 살펴봐야 할 것 같습니다.

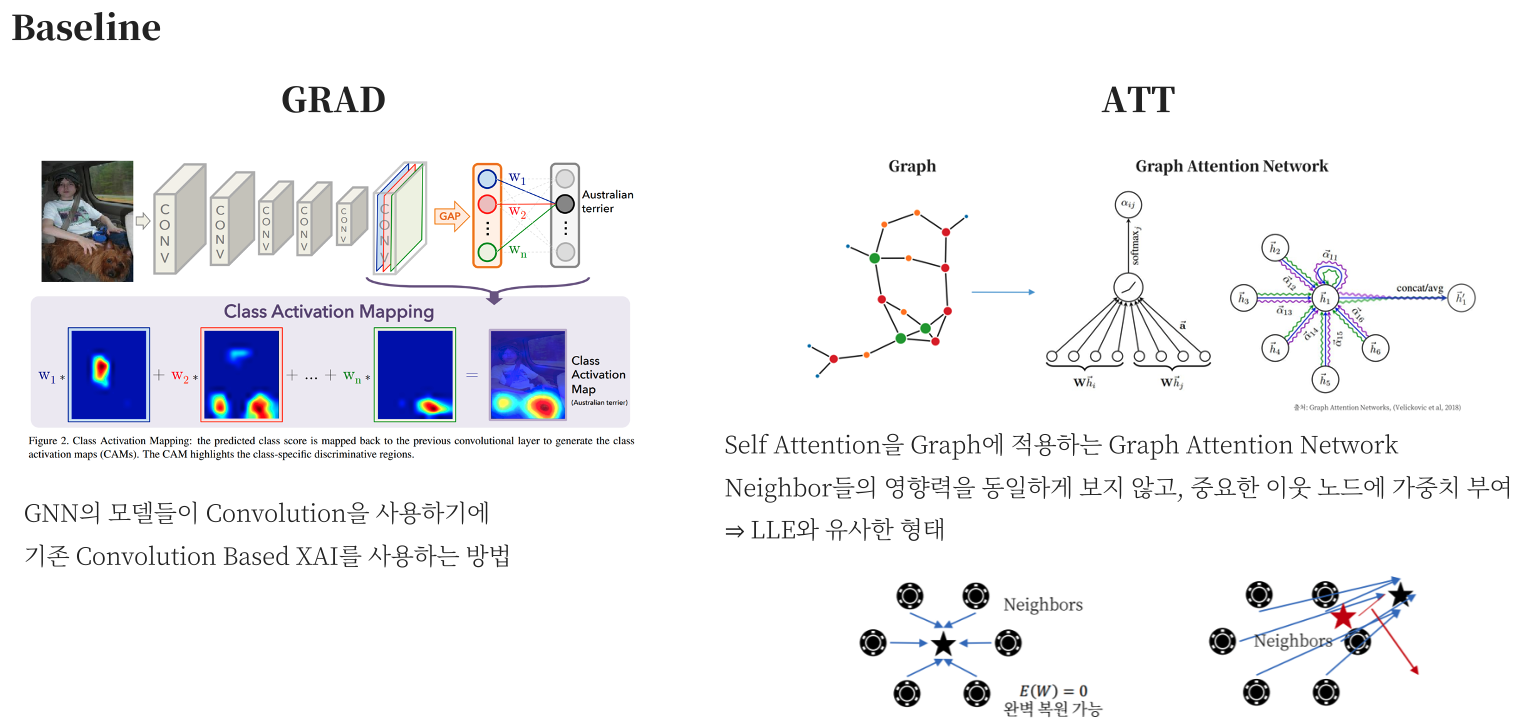
• GRAD
  • GNN Loss Function의 Gradient를 Adjacency Matrix에서 계산해내는데 Saliency Map을 구성하는 것과 동일하다.
• ATT
  • GAT를 통해서 Computation Graph의 Edge들에 대하여 가중치를 계산할 수 있는데 Feature에 대한 가중치는 알 수 없다.

Setup and implementation details

• 각 데이터 셋에 대하여 먼저 GNN을 적용하여 훈련
• GRAD / GNN Explainer를 통해 GNN의 예측값을 설명
• ATT는 GAT를 통해 Attention Weight를 구성
• $K_M, K_F$는 각기 Subgraph와 Feature Explanation의 Size를 나타낸다.
• Synthetic Dataset에서는 $K_M$을 Ground Truth로 설정
• Real Dataset에서는 $K_M = 10$으로 나타내며, $K_F$는 모든 데이터 셋에서 5

실험을 통해서 저자들이 밝혀내고자 한 질문들은 다음과 같습니다.

• GNN Explainer, 꽤 괜찮은 설명을 할 수 있는가?
• Ground-Truth Knowledge와 Explanation을 어떻게 비교하는가?
• Graph 기반 예측 Task에서 GNN Explainer를 어떻게 사용하는가?
• 훈련된 GNN말고 다른 GNN에도 바로 적용할 수 있는가? (Inductive)

Quantitative Analyses

Node Classification Dataset에 대한 Accuracy를 위의 표에서 확인할 수 있습니다. GNN Explainer를 통해 예측한 값은 무엇이고 Label은 무엇일까요?

• Predicted: Explainability Method으로 예측해낸 Importance Weights
• Label: Ground-truth Explanation에 포함되어 있는 Edge

즉, Ground-Truth Label을 예측해나가는 Binary Classification으로 문제를 정의해 나갔습니다. 더 우수한 Explainability Method는 더 정확히 Ground Truth Edge들을 예측해냈기에 Accuracy가 높게 나타납니다.

Qualitative Analyses

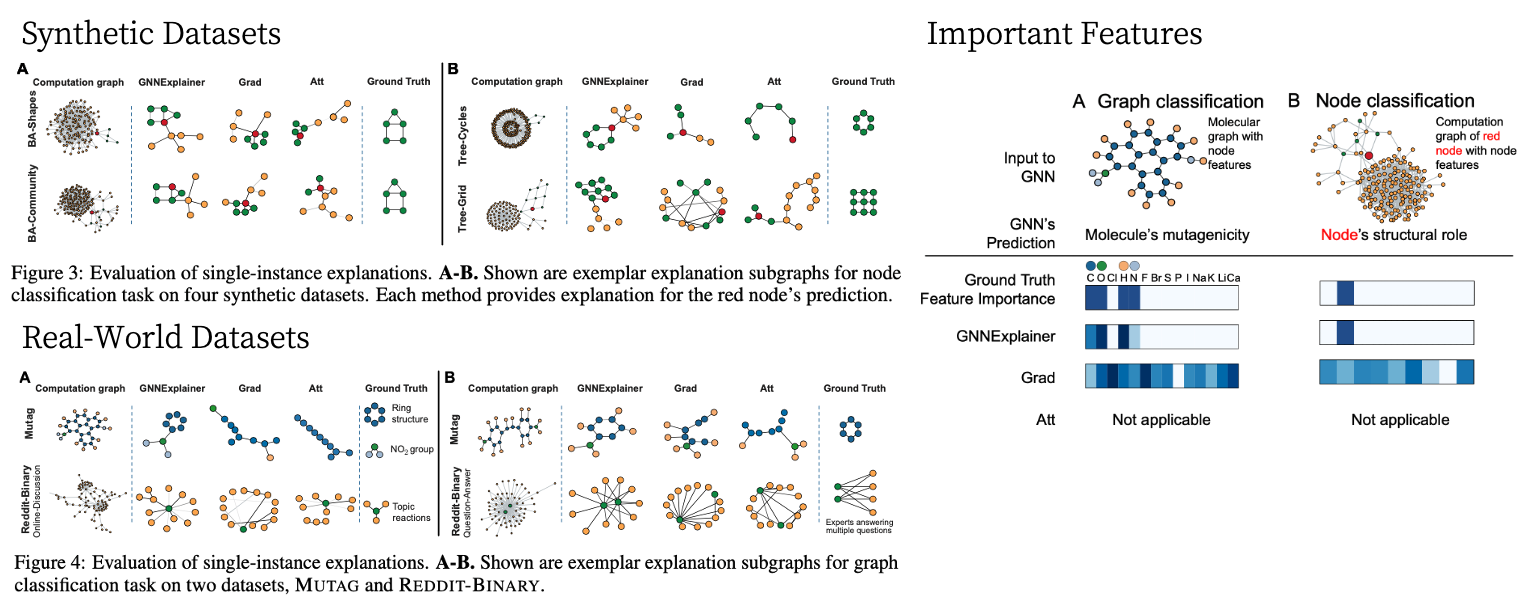
Synthetic Datasets의 Task를 다시 한번 살펴보자면, 먼저 노드들에는 4개의 Class가 있으며 해당 Class들을 맞추는 것이 목적입니다. 그리고 기본적으로 Base Graph에 연결되어 있는 Motif가 Explanation, 또는 Ground Truth라고 정의하고 있으며 이는 Figure 3에서 나타내고 있습니다. GNN Explainer는 정확하게 House / Cycle / Tree Motif들을 잘 예측해내어 하나의 노드를 설명하기 위한 Explanation을 탐지했으나, Grad나 Att 기법들은 제각각의 결과를 나타내는 것을 볼 수 있습니다.

Real World Dataset에서는 Graph Classification Task를 진행하는데, 하나의 전체 그래프를 판별하기 위해 필요한 Motif들을 Return 합니다. 따라서 GNN Explainer로 MUTAG 데이터셋에 적용했을 때, 각 Graph를 분류하기 위한 특정 Motif들을 잘 나타내지만, 다른 기법들은 Ground Truth와 거리가 좀 멀어보입니다.

REDDIT-BINARY Dataset에서는 Label이 각 그래프가 어떤 유형의 thread인지를 판단하는 목표를 갖고 있었습니다. QA thread를 보게 되면 2-3개의 높은 Degree의 노드가 다른 낮은 Degree의 노드와 많이 연결되어 있는 것을 볼 수 있습니다. 생각해보면, Reddit과 같은 커뮤니티에서 답을 하는 사람들은 소수의 똑똑한 사람들이기 때문이기에 일리가 있어보입니다. 따라서 그래프 자체의 Label을 판별하는 과정에서 어떤 Subgraph를 획득하는 과정을 통해 모델 자체를 설명할 수 있게 되는 것입니다.

확실하게 해야 할 것

모든 Graph Based [Model]은 목적이 있습니다. 그리고 이 목적은 Node Classifcation / Graph Classifcation 등 다양하게 나타날 것입니다. 하지만 헷갈리는 것이 있는데 이는 Ground Truth입니다.

• Synthetic Dataset $\Rightarrow$ Base Graph에 연결된 Motif

• Real-World Datasets $\Rightarrow$

  • MUTAG: 분자 구조를 구성하는 하위 요소를 다 알고 있으니 Ground Truth를 지정 가능
  • REDDIT: 각 thread의 일반적인 특징을 생각해서 정의

여기까지 해서 GNN Explainer에 대한 설명을 마칩니다. GNN Explainer는 XAI 분류 체계 내에서 Perturbation / Mask Generating Graph Explainer라고 할 수 있습니다.

특징으로는

• 중요한 Subgraph를 탐색하기 위하여 Variational Inference를 통해 Latent Distribution을 탐색하는데에 목적이 있으며,
• Single Instance Explanation은 가능하지만 Multi Instance Explanation은 활용성이 부족합니다.

GNNExplainer는 차후에 문제점이 여러 개 나타나며, 후속 논문들에서 이를 보완하기 위하여 많은 노력들이 가해지는데 GNN XAI의 최초의 논문이기에 함의점이 매우 큽니다. 이는 후속 논문들의 Baseline 역할을 하면서 GNN XAI를 어떻게 연구하고 실험을 해야할 지에 대한 Guideline을 제공했다고 할 수 있습니다.