CS224W 4번째 강의 정리를 정리해보았습니다. 강의에서 사용된 이미지 전체는 CS224W 수업 자료에서 가져왔음을 미리 밝히는 바입니다.

이전 강의에서는 각 노드의 Role에 대해서 알아봤으며, 이와 연관된 Community 개념에 대해서 존재만 안내했었습니다. 4장에서는 Community의 특징에 대해서 설명하였으며, 이를 정리해보겠습니다.

Network & Communities

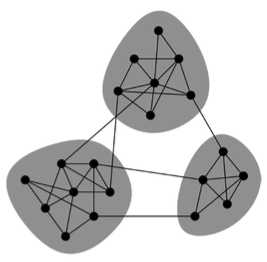
위와 같은 네트워크 그림을 보게 되면, 그 안에 존재하는 Subgroup이 Community라는 것입니다. 즉, 노드들의 집합이라고 말할 수 있으며, 강의에서는 이에 대해서 먼저 설명하지 않고 본격적으로 Community를 설명하기 전에 사전 지식을 전달합니다.

사람들은 어떻게 직업을 찾을까?

Mark Granovetter라는 사회학자는 다음과 같은 질문을 해소하고자 했습니다.

사람들은 어떤 경로로, 어떤 방식으로 자신의 직업에 대한 정보를 찾을까?

물론 요즘에는 ‘사람인’ 등과 같은 다양한 취업 정보 사이트가 많았지만, 조사를 진행할 당시에는 입으로 전해지는 정보들이 사람들의 취업에 영향을 끼쳤을 것입니다. 따라서 간단하게 생각해보면 매일 만나는 친구나 가까운 관계를 유지하는 사람들로부터 정보를 얻겠다는 생각이 들겠지만 조사 결과 ‘Close Friends’가 아닌 ‘Acquaintance’로부터 정보를 얻는 비율이 더 높았다고 합니다. (물론 이것은 미국과 같은 나라에서만 가능하다고 생각하는 것이, 그들은 “파티 문화”가 매우 많기에 그러지 않나 싶습니다)

그렇다면 왜 밀접한 사이가 아니라 일면식만 있는 정도의 ‘Acquaintance’들로부터 정보를 많이 얻게 되는 것일까요? 이를 파악하기 위해선 “Friendship”을 정의하는 관점을 살펴봐야 하며, 강의에서 말하는 “Friendship”이란 Graph의 Edge를 뜻하는 것입니다.

Two Perspective on Friendship

Structural: “Friendship”이 그래프의 어떤 부분과 연결되는가? Structural은 Friendship 또는 Edge의 기능적인 면을 표현하며, Edge가 다른 사람들 또는 다른 커뮤니티를 알 수 있는 창구로서 역할을 합니다.
Interpersonal(social): “Friendship”은 두 사람 사이의 관계를 뜻하며, “Strong” or “Weak”로 강도를 표현할 수 있다. Interpersonal은 좀 더 보편적인 개념인 관계의 강도라고 생각하시면 됩니다.

Friendship의 Structural role의 예시로는 Triadic Closure가 있습니다.

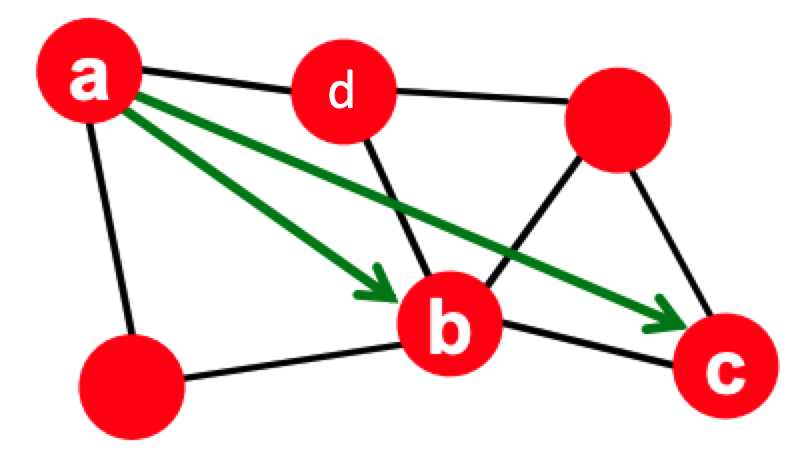
Triadic closure의 정의는 다음과 같이 표현할 수 있습니다.

네트워크 내의 두 사람이 공통의 친구가 있다면, 두 사람도 친구가 될 가능성이 높다!

Triadic을 Sturcural role이란, 위의 그래프에서 a가 b와 연결 가능성이 높은 이유가 d라는 공통 친구가 있어서이며, 이 때 d가 a와 b 사이의 관계 연결의 창구가 되어주었기 때문입니다.

Graph의 Node와 Vertex가 혼용되듯이, 해당 강의에서도 용어의 혼용이 있어서 헷갈리기에 social = interpersonal’이라는 것을 기억해두셔야 합니다

Granovetter는 위에서 소개한 Structural / Interpersonal(social)간의 관계를 정리하였습니다.

Structure Point of View
- Structurally embedded edges are also socially strong
  
  “구조적으로 잘 짜여진 Edge는 Social 관점에서도 강하다”: Structurally Embedded가 처음에는 무슨 말인지 잘 와닿지 않았는데, Edge의 기능 두 가지가 ‘연결’과 ‘연결의 강도를 표현’이라는 느낌으로 생각했을 때, Structurally Embedded는 연결의 의미를 강조하므로 노드들간의 Densely Connected 되었다는 의미로 받아들였습니다. 강하게 연결된 Connection들 사이에서는 Interpersonal 관계가 높을 것입니다.
- Long-range edges spanning different parts of the network are socially weak
  
  반면, Network의 다른 부분으로 이동할 수 있도록 하는 Long-range Edge들은 Socially Weak 할 것입니다.
Information Point of View
- Structurally embedded edges are heavily redundant in terms of information access
  
  Densely Connected 노드들은 확실히 사회적으로 똘똘 뭉치게 될 것입니다. 하지만 예를 들어, Graph Theory 공부만 매일하는 친구들과 계속 이야기를 나누다보면, 해당 개념에 대한 이해는 완벽할지 몰라도 다른 개념을 혼합하여 더 좋은 성능을 낼 수 있는 ‘Breakthrough’를 생각해내기 어려울 것입니다. 즉, 다양한 정보를 취득하기 어려운 구조라는 것입니다.
- Long-range edges allow you to gather information from different parts of the network and get a job
  
  반면, 사회적으로는 강하기 연결되진 않았어도 전체 네트워크의 먼 곳까지 이어줄 수 있는 Long-range Edge들은 하나의 노드가 방문할 수 있는 범위를 늘려, 한 사람의 식견의 범위를 넓혀주기에 정보 취득에 용이할 것입니다.

Triadic Closure = High Clustering Coefficient

Clustering Coefficient에 대한 정의를 복기해보면, ‘이웃간의 연결 강도’라고 할 수 있습니다. 즉, 자신을 제외한 나머지 노드들끼리의 관계가 어떻게 되느냐를 판단하는 것입니다.

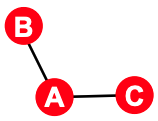
따라서, 위와 같이 Triadic Closure를 생각해보면, A로 인해 B와 C가 만나게 되고 친해지게 될 것이므로, B / C간의 Edge가 생길 것이며 이로 인해, Clustering Coefficient가 증가할 것입니다.

위에서부터 쭉 정리하며 내려온 Granovetter의 이론은 사실 검증이 되지 않았습니다. 실질적으로 이를 실험해볼만한 데이터셋을 구할 수 없었던 것이 원인인데, 2000년대에 들어서 기술의 발전으로 이를 검증할 수 있게 되었습니다.

Onnela et al.은 EU 국가의 20%의 통화 기록을 통해 실험을 진행하였으며, 이 때의 Edge Weight는 ‘상호간 얼마나 전화를 하였는가’ 였으며 이는 Interpersonal 한 Strength입니다. 하지만 이에 더하여 Edge의 Structural Strength도 함께 살펴보기 위하여 Edge Ovelap이라는 개념을 정의하였습니다.

실험 결과를 보기 전에, Edge Overlap 이라는 개념에 대해서 짚고 넘어갔습니다.

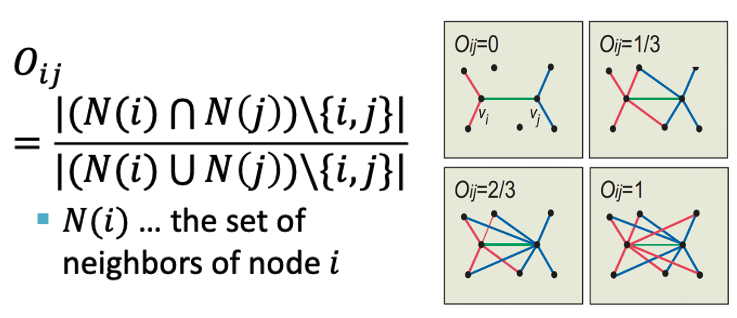
Edge Overlap이란

두 노드가 공통적으로 연결하고 있는 노드; 얼마나 Mutual Friend를 갖고 있는가?

를 뜻하며, 위에서 식과 그림 예시를 표현해놨습니다. Structural / Interpersonal Strength를 비교해서 살펴보자면, 아래 그림과 같습니다.

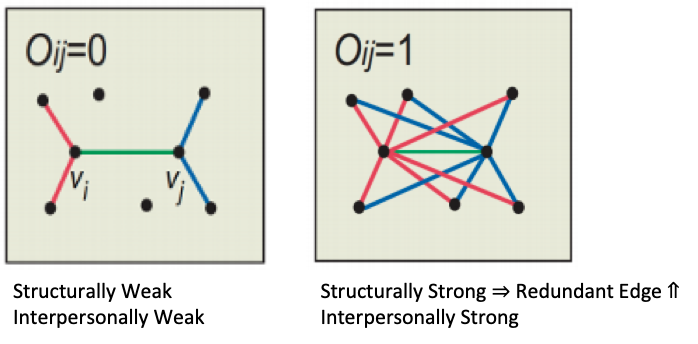
왼쪽의 Edge Overlap이 0인 경우에는 초록색 선이 Local Bridge의 역할을 하여, 공통 친구가 없는 두 집단을 연결해주는 역할을 합니다. 물론 Edge Overlap이 큰 경우에도 초록선이 존재하지만 Local Bridge의 역할을 하지는 않습니다. 특징으로는,

Overlap = 0: Green Line의 통화 빈도가 적다.
Overlap = 1: Green Line의 통화 빈도가 높다.

와 같이 나타낼 수가 있습니다. 이를 통해 Strutural tie와 Interpersonal tie의 관계를 정의해낼 수 있었습니다.

실험 결과

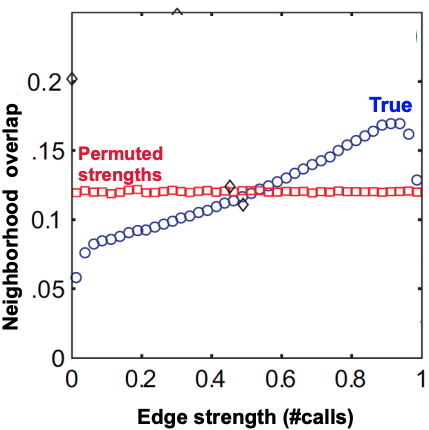
실험 결과, Edge Strength가 높을 수록, 즉 통화 빈도가 높은 관계일수록 Edge Overlap이 높아지는 것을 볼 수 있습니다. 하지만 이것이 우연의 결과가 아님을 증명하기 위하여, Network Structure를 유지한 채 Edge Strength를 재배치한 Null Model 과의 비교를 해보았더니, Null Model은 비례 관계가 유지되지 않았습니다.

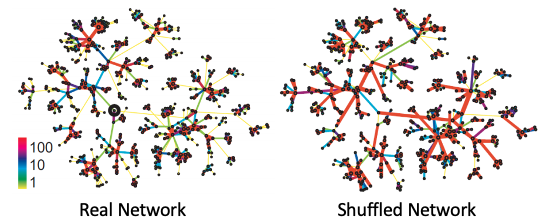
좀 더 실제 Graph Edge에 대한 Visualization을 살펴보면 위와 같습니다. 좌측은 실제 네트워크의 Edge를 강도에 따라 색깔별로 표시한 것이며, 우측은 구조만 같게한 채 Strength를 Random Shuffle한 것입니다. 특징으로는,

Real Network에서 하나의 Community의 중심점을 맡고 있는 Node들의 Edge들은 Strength가 강하게 표현되어 있다.
하나의 Community에서 다른 Community로 이어지는 Edge는 Strength가 약하게 표현된다.

지금까지 설명했던 Edge들의 여러 특성을 통해 또다른 실험을 진행되었습니다.

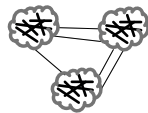
다음과 같은 Cluster를 이루고 있는 Graph에서 Strength가 강하면 Community 내의 Edge일 것이고, 약하면 Community 끼리를 잇는 Edge일 것입니다. 따라서 Strong Edge를 순차적으로 없애는 행위는 Community를 부수는 것이 빠르게 진행되지 않을 것인데, 그 이유는 애초에 Densely Connected이기 때문입니다. 하지만 Weak Edge를 순차적으로 없앤다면, 전체적인 구조가 빠르게 부서질 것입니다.

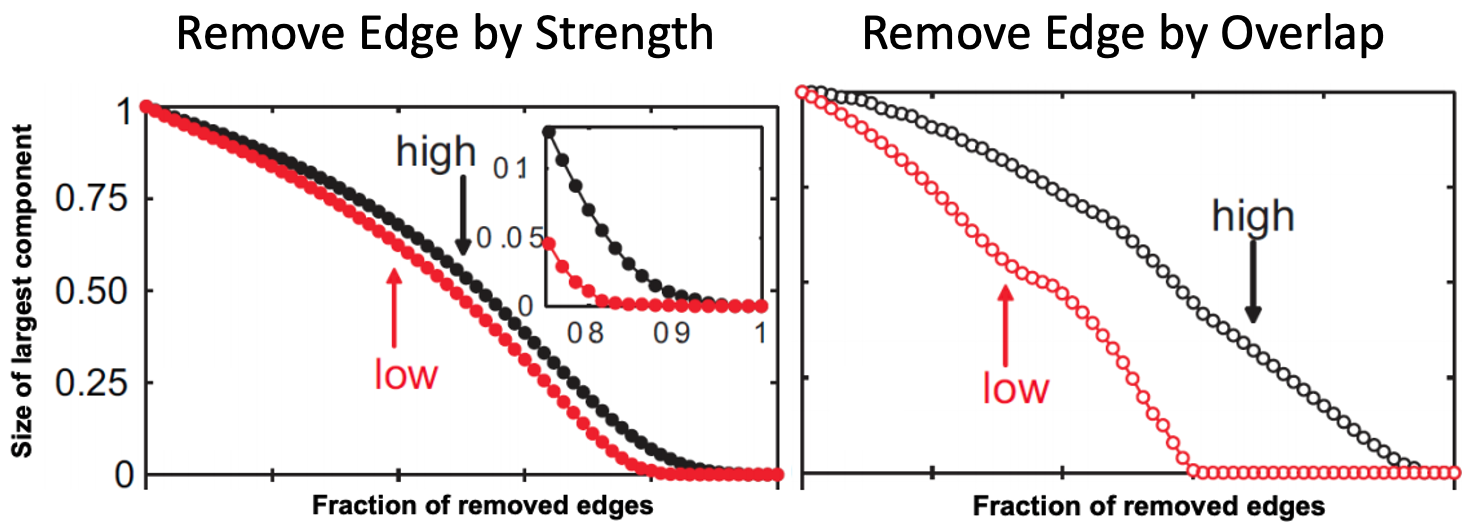
위의 그래프는 Edge를 순차적으로(오름차순: low / 내림차순: high) 제거해나갈 때, Largest Component의 Size가 어떻게 변하는 지 살펴보는 것입니다. Size of Largest Component가 감소할수록 전체적 구조가 일그러진다고 생각해본다면, 두 그래프 모두 Low Strength / Overlap을 먼저 삭제하는 것이 빠른 감소로 나타났으며, 감소의 폭은 Strength보다 Overlap에서 더 크게 나타났습니다.

Granovetter’s Theory 정리

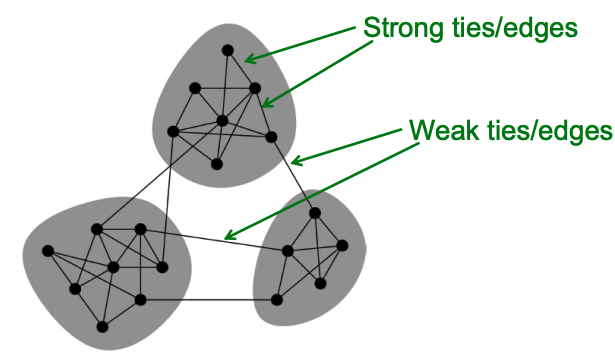
Granovetter의 이론을 정리하면 다음과 같습니다.

Community 내의 Edge는 Strong Structural / Interpersonal Edge, High Edge Overlap
Community를 잇는 Edge는 Weak Structural / Interpersonal Edge, Low Edge Overlap
사회학자가 정리한 이론이며 실험도 Social Network에 적용해 도출한 결론이지만, Graph 전체에 적용되는 이론이다.

Network Communities

위의 Geranovetter 이론을 토대로 한다면, Network는 강하게 연결된 노드들의 집합이며, Network 내의 Internal Connection이 많고, 적은 수의 External Connection이 있습니다. 그럼 이제는 다음과 같은 문제를 풀 때입니다.

자동적으로 밀접하게 연결된 Node 집단을 어떻게 찾는가?

Example: Zachary’s Karate club network

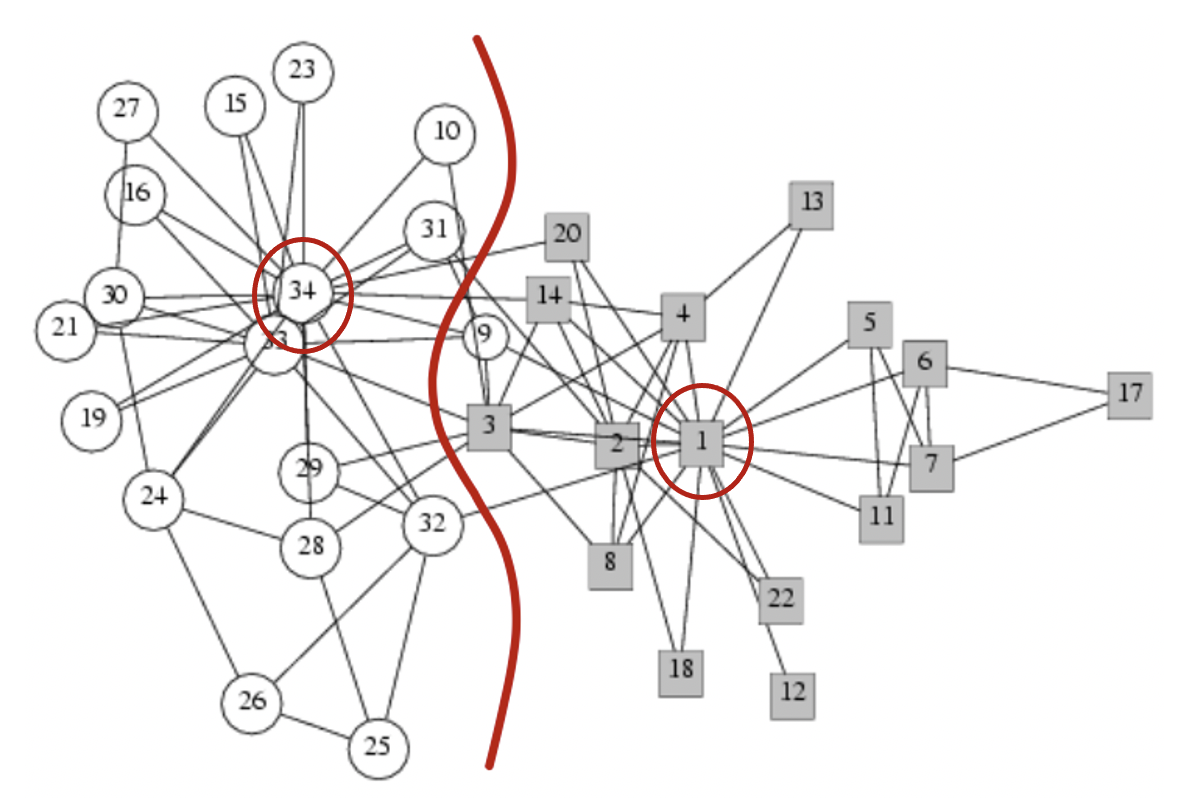
해당 예시는 뭔가 웃픈 썰이 포함되어 있는 네트워크로서, Wayne W. Zachary의 “An Information Flow Model for Conflict and Fission in Small Groups” 논문에서 예시로 사용된 Social Network입니다. 이는 대학 내의 Karate Club 내에서 발생한 Social Network 분화 예시인데, 아쉽게도 어느 대학교인지는 명시가 되어있지 않습니다. 간단하게 포함된 이야기를 전달드리자면, 34명의 Karate club member들 중 Administrator “John A”와 Instructor “Mr.Hi (가명)”간에 갈등이 발생한 후, “Mr.Hi”파와 “비 Mr.Hi”파로 나뉘게 된 사건입니다. 이로 인해, 위의 그래프를 살펴보면, 1번 중심의 Network와 34번 중심의 Cluster가 형성된 것을 볼 수 있으며, Edge들로 학생들간의 관계를 표현한 것입니다. 이 때, 그래프의 Structure를 통해 특정 멤버가 두 집단 중 어떤 집단으로 흘러 들어갈지 예상할 수 있습니다.

Modularity

자동적으로 밀접하게 연결된 Node 집단을 어떻게 찾는가?

이 문장에서 “밀접하게 연결된”이라는 말에 대해서 정의를 내려야합니다. 이는 Modularity로 나타내며 이름에서 특징을 유추할 수 있는데, “얼마나 잘 Module화”되어 있는가, 즉, Network가 Community들로 잘 나누어져 있는가에 대한 정의입니다.

Modularity는 Q로 나타내며, Network를 disjoint community $s\in S$로 나눌 수 있다고 할 때,

위와 같은 식으로 나타낼 수 있습니다. 즉, 풀어서 나타내보면

Network 내의 Community들에 대하여, Community 내의 Edge 개수와 Null Model의 Expected Edge 개수의 차로 Modularity를 나타낸다.

라고 표현할 수 있으며, 예상보다 실제의 Cluster 내의 Edge 값이 클수록 Community가 잘 구성되었다는 뜻입니다. 그럼 이 개념을 정립하기 위하여 Null Model인 Configuration Model을 생성해야 합니다.

Louvain Algorithm

지금까지는 Network의 Community가 잘 생성되었는지에 대한 Evaluation만 진행하였으며, 이는 Modularity로 가능했습니다. 그렇다면 실제로 Community를 탐색하는 과정은 어떻게 되는지 알아볼 것이며 먼저 Louvain Algorithm을 살펴보겠습니다.

Louvain Algorithm 특징

알고리즘의 난도가 그렇게 크게 어렵지 않기 때문에 특징을 먼저 서술하겠습니다.

계산복잡도: $O(nlogn)$
Greedy Algorithm for community detection
Weighted Graphs 사용 가능하다.
Hierarchical Community를 표현할 수 있다.
특히 Large Network에 많이 사용되는데,
- 수렴 속도가 빠르고
- 높은 Modularity output을 return한다.

Louvain Algorithm은 “탐욕적으로(Greedily)” Modularity를 최대화하는 과정으로 진행됩니다. 한번의 Pass 당 2개의 Phase를 거치게 되는데,

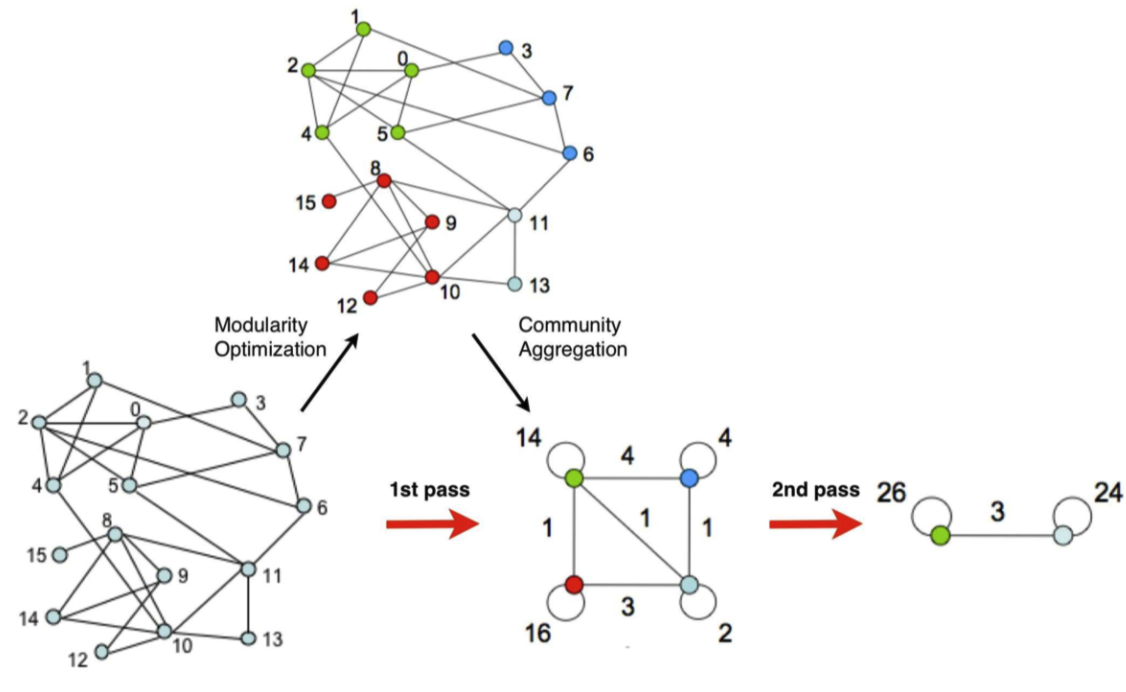
Phase 1: Modularity Optimization 하나의 Node의 이웃들에 대하여 Community를 형성하여 Modularity를 Update한다.
Phase 2: Community Aggregation Phase 1에서 생성한 Community를 모아모아 Super node를 형성하여 새로운 Network를 생성한다.

위의 그림에서 살펴보면, Phase 1 / 2를 통과한 것이 1st pass를 거친 것임을 표현하고 있습니다. 해당 Pass들은 더 이상 Community를 생성함으로써 발생하는 Modularity의 증가가 나타나지 않을 때 더 이상 진행하지 않게 됩니다.

Louvain Algorithm에 대하여 간단하게만 알고 싶다면, 지금부터 설명하는 수식에 대해서 빠르게 넘어가셔도 됩니다.

Louvain Algorithm 빨간맛

Graph 내의 모든 노드를 Distinct한 Community로 간주한다. (노드당 1 Community)
각 노드 $i$마다, 다음의 계산을 진행합니다.
- $i$를 이웃 $j$의 Community에 포함시켰을 때, Modularity Delta ($\Delta Q$)를 계산한다.
- $\Delta Q$의 변화량이 가장 큰 $j$의 Community에 $i$를 포함시킨다.
- 이런 방식으로 진행할 경우, 당연히 순서에 의해 구성되는 Cluster가 다를 수 있는데 연구 결과, 순서가 큰 영향을 주지는 않는다고 한다.

결과적으로 풀어서 적어보자면, Node들이 현재 속한 Community에서 다른 Community로 소속을 변경했을 때의 Modularity Gain을 구해야 하며, 하나의 노드들이 소속이 없을 때도, 개별적으로 Community를 형성하므로, 소속 변경의 의미가 유지가 됩니다.

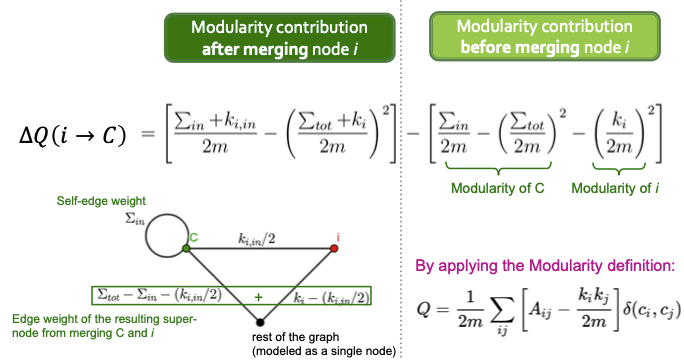
$i$ 노드가 $C$로 소속 변경을 했을때, Modularity의 변화 또는 Gain은 위의 식으로 표현할 수 있습니다.

Detecting Overlapping Communities: BigCLAM

지금까지 살펴본 Louvain Algorithm은 Non-overlapping Communities에 적용되는 알고리즘입니다. Overlapping과 Non-overlapping community의 차이를 살펴보면 아래의 그림과 같이 ‘겹치는 부분’이 존재하느냐, 그렇지 않느냐의 차이입니다.

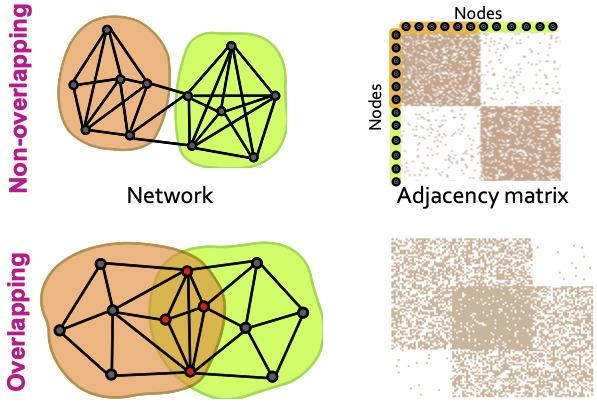
두 Community Overlapping 차이는 Adjacency Matrix에서도 나타나며, 해당 Matrix도 Overlapping의 유무로 차이를 비교할 수 있습니다.

즉, Louvain에서는 Overlapping을 다루지 않기에, 저 중간의 빨간 노드들에 대하여 정의를 내릴 수 없으며, 분명 겹치는 노드들이지만, 계산 상 둘 중의 하나의 Community에 Discriminative하게 포함이 될 것입니다 (0/1). 따라서, BigCLAM Model에서는 Community Affiliation Graph Model (AGM)이라는 Generative Model을 구축한 뒤에, 해당 모델을 통해 Node들의 Community를 지정하여, Communities를 그리게 될 것입니다. Affiliation이라는 단어 뜻이 ‘제휴’라는 뜻이므로, 겹치는 부분에 대한 정의를 내포하고 있음을 알 수 있습니다.

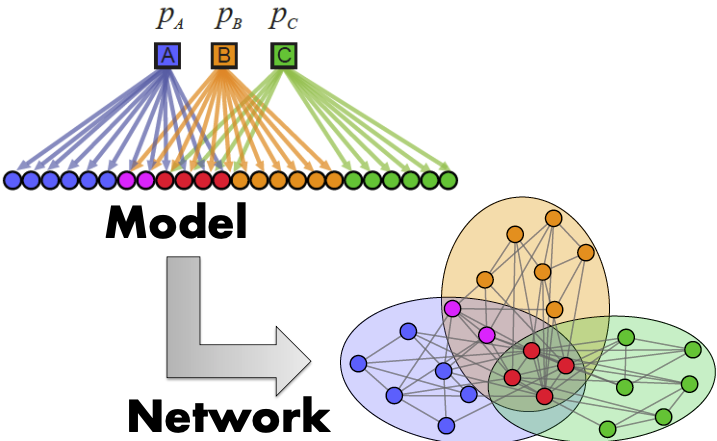
먼저 개괄적으로 AGM의 절차에 대해 안내해 드리자면 다음과 같습니다.

Step 1 Node Community Affiliations, 즉 Community간의 교집합에 기저한 Generative Model을 정의한다 $\Rightarrow$ Community Affilication Graph Model(AGM)
Step 2
- Graph G가 존재할 때, AGM으로 G가 생성되었다는 가정 아래,
- G를 생성했을 가장 좋은 AGM을 찾는다.
- 이를 통해 Community를 찾을 수 있다.

AGM으로 표현되는 Generative Model은 Parameter $(V, C, M, [{p_c}])$를 갖고 있습니다.

$V$: Vertex
$C$: Community
$M$: Membership - Vertex가 어떤 Community에 Member인가?
$[{p_c}]$: 각 Community $c$ 내에 있는 노드들은 $p_c$의 동전 던지기 확률로 서로를 연결한다. 이 중 여러 Community에 Membership을 갖고 있는 Node는 Membership만큼 동전 던지기를 할 수 있다.

이를 통해 하나의 Community 내에 있는 Node $u,v$가 연결될 확률 $p(u,v)$는 다음과 같이 표현할 수 있습니다.

$p(u,v) = 1- \prod\limits_{c\in M_u \cap M_v} (1-p_c)$

해당 식을 읽어보면, 일단 $c\in M_u \cap M_v$가 있기 때문에 두 노드 $u,v$ 간의 멤버십이 교집합인 cluster에 대하여, 곱 연산을 합니다. 따라서, $u,v$ 가 같은 Cluster에 있는 경우가 많다면, 그 숫자만 $p_c$를 포함한 확률 곱을 진행할 것이고, $p_c$의 값이 크다면, 해당 확률 곱의 값이 작아테고, 전체 $p(u,v)$가 커질 것이며 vice versa입니다.

위의 과정은 사실 최적의 모델이 존재한다고 가정했을 때, 해당 Generative Model을 통해 Graph를 생성하는 과정이었습니다. 하지만 이는 최종 결과이며, 저희는 처음에는 AGM과 같은 모델은 구축해야 하는데 이것은 수중에 있는 Graph로 제작해야 합니다. 즉, Graph가 주어졌을 때, 모델을 구축하는 과정은 포함되어 있는 파라미터를 추정해나가는 과정으로 진행됩니다.

이는 Maximum Likelihood Estimation으로 가능합니다.

해당 MLE 식에 대한 과정은,

Parameter set $F$를 통해 모델을 구축한 뒤
해당 모델로 Graph가 생성될 확률이 가장 클 떄의
argmax이므로 $F$를 Return하라!

입니다.

즉 위와 같이, $P(u,v)$도 결국 $p_c$가 존재하면 구할 수 있는 파라미터이므로 $F$라고 간주한다면, 이를 MLE에 G와 함께 포함시켜 $P(G|F)$로 나타낼 수 있습니다.