Graph Convolutional Network (GCN)

Semi-Supervised Classification with Graph Convolutional Networks - Thomas N.Kipf, Max Welling / ICLR 2017

안녕하십니까. 고려대학교 산업경영공학과 석사과정, DSBA 연구원 윤훈상입니다. 이번 Paper review에서는 Graph Convolutional Network에 대해서 알아보고자 합니다. 본 논문을 리뷰하면서, 제가 이해하지 못한 개념 위주로 정리를 하면서도 번역도 겸하여 진행하고자 했기에, 논문의 목차를 따라가면서 서술했습니다.

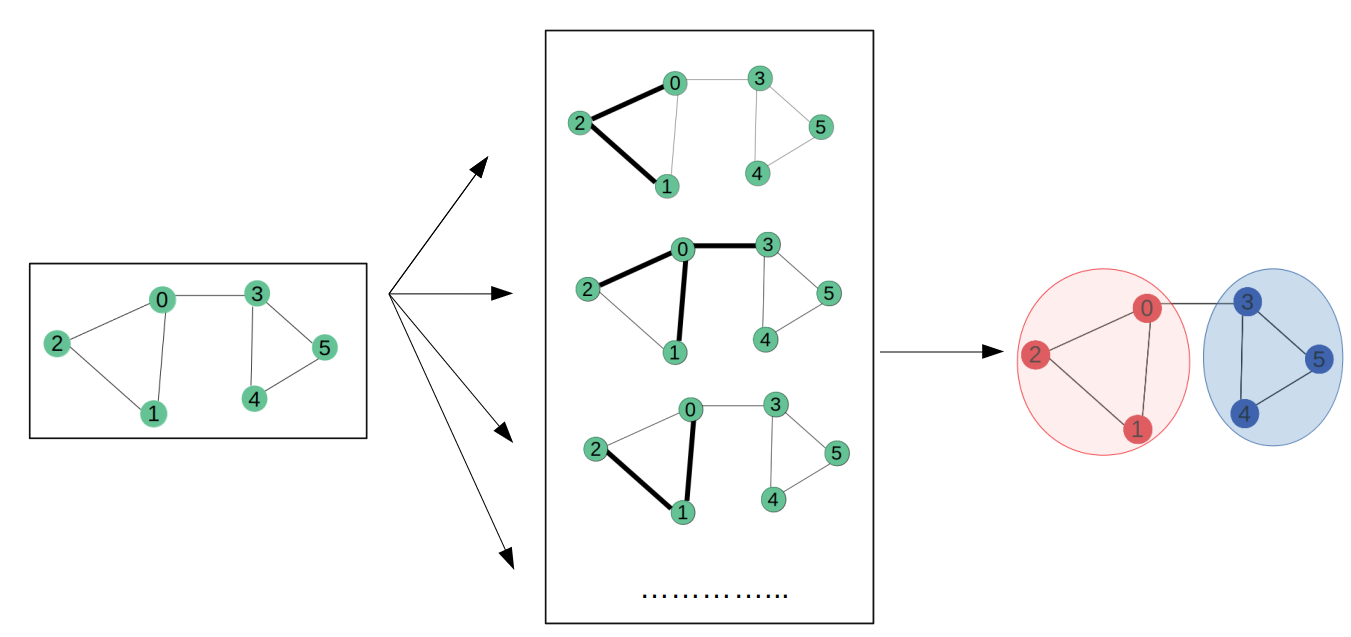
Background

Graph Neural Network (GNN)

맨 처음 GNN의 존재를 알았을 때, 처음으로 든 생각은 GNN은 Neural Network와 대응된다는 것이었습니다. 따라서, GNN이 기반으로 존재하고 각각 상황에 맞게, 이미지를 처리할 때는 Conv-GNN을, Sequence Data를 처리할 때는 Rec-GNN을 사용하는 줄 알았으며 이에 GNN이라는 알고리즘이 따로 존재하는 듯 하였습니다. 하지만 Survey 논문을 읽어본 결과, GNN은 단순히 하나의 특정 알고리즘을 칭하는 것이 아니라 Graph를 Input으로 활용하고 이를 분석하기 위하여 사용되는 모든 Neural Network기반 알고리즘을 GNN이라고 칭하는 것이었습니다.

GNN으로 달성하고자 하는 목적은 일반적인 Dataframe보다 객체간의 관계를 더 잘 반영하는 데이터 꼴인 Graph를 입력으로 사용하여 Neural Network를 통과시켜 Node, Edge 또는 Graph 자체에 대한 Classification을 하는 것입니다. 역사적으로 살펴보자면, Recurrent GNN이 먼저 사용이 되었으며, 이어 GCN / GAE / STGNN과 같은 다양한 Variation들이 나타났습니다.

Convolutional Neural Network (CNN)

CNN은 이미 많은 분들이 아실거라 생각하여 간략하게만 서술하자면, 주로 이미지 데이터에 많이 쓰여, Kernel / Filter를 사용해 전체 이미지를 순회하여 픽셀의 정보를 Aggregate하는 과정을 거치는 기법을 말합니다. 저는 RNN을 공부하면서, Recurrent이라는 단어가 기법을 매우 잘 표현하고 있다고 생각했지만, Convolution에 대해서는 딱히 생각을 해본 적이 없습니다. 하지만 본 GCN을 이해함에 있어 Convolution이라는 개념에 대해서 알 필요가 있습니다.

Convolution

Convolution은 깊게 들어가면 범위가 매우 커 간략하게만 언급하자면 “두 함수의 합성곱”입니다. 식의 꼴로는

$f \star g = (f * g)(t) \int_\infty^\infty f(t)g(t-\tau) d\tau$ 로 나타낼 수 있습니다.

정의: 두 함수 f,g가운데 하나의 함수를 반전, 전이 시킨 다음, 다른 하나의 함수와 곱한 결과를 적분하는 것을 의미한다.
풀이: 현재 시점의 합성곱의 값은 이전시간의 결과를 포함하여 구성된다.

정의는 Wikipedia에서 가져온 것이나 이를 저 나름의 풀이를 진행한 것이 정의 아래 나타나 있습니다. 이는 확실히 난해하여 예시를 통해 살펴 보겠습니다.

재야의 종소리 참고: 네이버 블로그

2020년은 ‘대 코로나 시대’로 였기에 아쉽게도 한 해를 마무리 하는 재야의 종소리를 실제로 보지 못하였습니다. 하지만 해당 종소리는 많은 분들이 익히 기억나실거라 생각합니다. 종을 맨 처음 ‘둥’치면 해당 타격에 의한 소리가 크게 울리면서 점차 감소할 것이며, 이는 아래의 꼴과 같습니다.

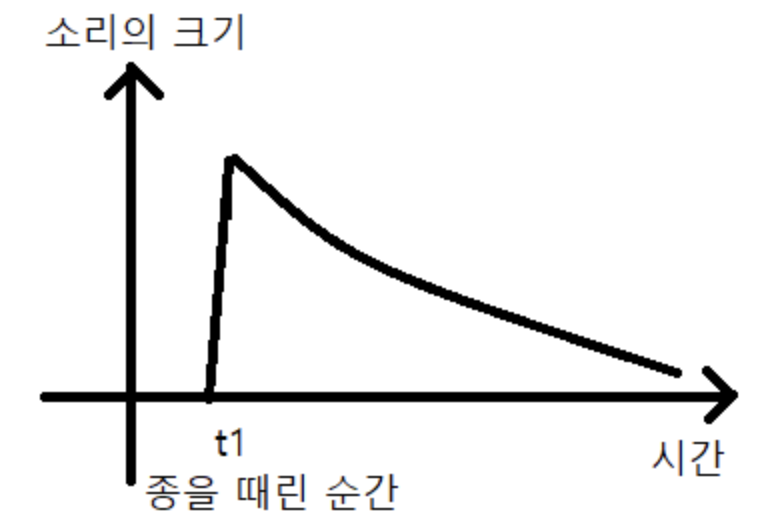
그럼 이번에는 종을 두 번째로 치는데 처음 타격보다 약간 작게 치도록 하겠습니다.

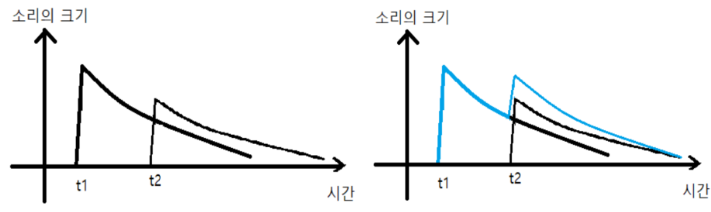
두 번째 종소리는 첫 번째 종소리보다 작을 것이며 이는 위의 그림과 같이 표현할 수 있습니다. 그렇다면 우리의 청력은 두 소리를 완벽하게 구분할 수 없으므로, 두 소리가 합쳐진 소리가 들릴 것이며 이는 우측 그림의 파란색 선으로 표현할 수 있습니다. 따라서 하나의 함수 결과를 return하기 위하여 두 함수가 합쳐지는 것을 볼 수 있으며, 파란색 선이 합성곱의 결과라고 할 수 있습니다.

확실히 개념이 생각보다 복잡하여 이만 줄이고자 하지만, 핵심은

“Convolution이 이미지에서만 사용되는 개념이 아니며 더 광범위하게 사용되는 것”임을 알아 두셨으면 좋겠습니다. 이는 이미지 데이터가 아닌 Graph 데이터에 Convolution을 적용하는 것에 대하여 이해할 수 있는 수단이 될 수 있기 때문입니다.

Graph Convolution

그럼 이제 Convolution이 Graph에 왜 필요한지에 대해서 생각을 해봐야 합니다. 그래프는 매우 유기적인 데이터 구조입니다. 하나의 노드는 단순히 자기 자신으로만 존재하는 것이 아니라 다른 이웃 노드들의 존재에 의해서 정의됩니다. 마치 사회의 일원처럼 말입니다. 따라서 Convolution과 같이 자신(Central Node) 주위에 있는 이웃 노드들의 정보를 한 데로 Aggregate하는 과정이 해당 연산을 빠르게 처리해줄 것이기에 합성곱 연산이 필요한 것입니다.

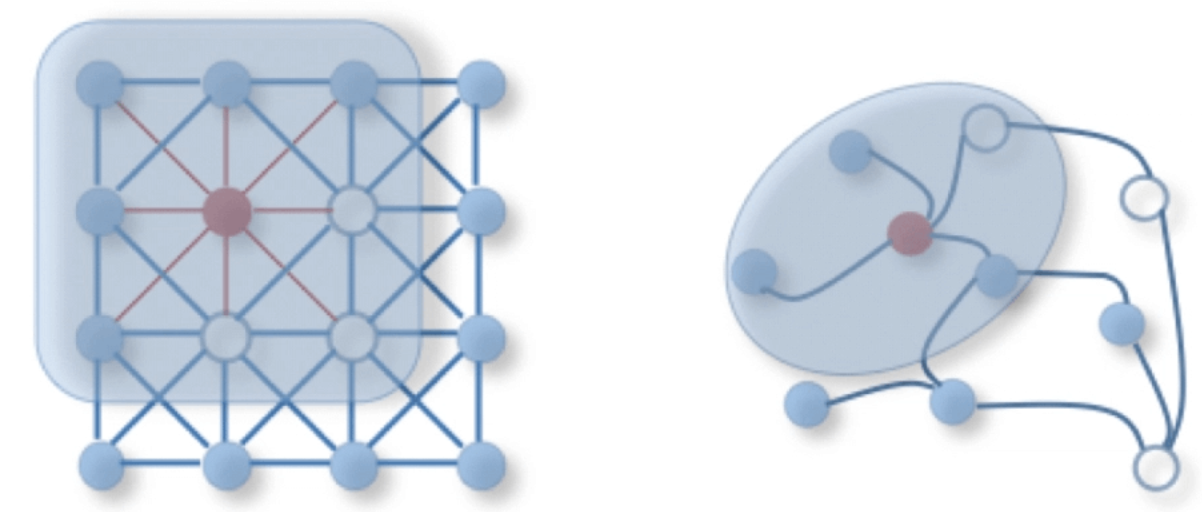
위의 그림은 좌측이 이미지 데이터에 대한 Convolution / 우측이 Graph Convolution을 나타냅니다. Convolution Filter는 본디 모든 데이터에 공통으로 사용되므로 regular grid형태로 나타납니다. 일반적인 CNN의 Filter를 생각해보면 알 수 있습니다. 하지만 우측의 Graph에서 살펴보게 되면, 일단 Grid 형태가 아닌 것은 차치하더라도, 모든 노드가 자신의 이웃에 대하여 Convolution Filter를 씌울 때, 해당 Filter의 크기가 모두 제각각일 것입니다.

하지만 Convolution은 Graph에 사용하기를 포기하기엔 매우 좋은 특징들을 갖고 있습니다.

Convolution을 통해 전체 데이터에서 Local Feature를 뽑아낼 수 있다.
Filter들이 Spatial Location에 따라 변하지 않는다.

따라서 Convolution을 Graph에 적용하기 위해 Convolution Theorem을 사용하고자 합니다. Convolution Theorem이란 다음과 같이 정의됩니다.

한 Domain의 Convolution은 다른 Domain의 Point-wise Multiplication과 같다
Graph Domain의 Convolution은 Fourier Domain의 Point-wise Multiplication과 같다.
Convolution의 Laplace 변환은 Point-wise Multiplication으로 변한다.

Convolution Theorem을 기반으로 Graph 내에서는 Convolution을 진행할 수 있게 되며, 이는 Fourier Transform을 기반으로 진행되게 됩니다.

Introduction

본 논문에선 제목에서 살펴볼 수 있듯이, Semi-Supervised Classification, 즉 Labeled / Unlabeled Data가 공존할 때, 두 데이터를 함께 활용하여 분류 문제를 진행하고자 하는 것이며 일반적으로 Labeled Data 쪽이 수가 더 적습니다.

$L = L_0 + \lambda L_{reg}, with \ L_{reg} = \sum_{i,j} A_{ij} |f(X_i ) - f(x_j)|^2 = f(X)^T \Delta f(X).$ ~(1)

Notation:

$L_0$: Graph의 Label이 존재하는 데이터의 supervised loss
$f(\cdot)$: 미분 함수가 포함된 Neural Network
$\lambda$: weighting factor
$X$: 노드들의 feature vector를 담는 $X_i$들의 행렬
$\Delta$: $D-A$ 로 나타내며 Graph의 Unnormalized graph Laplacian

(1)번 수식으로 표현된 Loss Function은 결국 연결된 노드들은 같은 Label을 가질 것이라는 가정을 갖고 있습니다. 이 가정은 Label Smoothing의 역할을 하게 되며, $L_{reg}$가 그 역할을 하는 것입니다. 하지만 해당가정은 모델의 Capacity를 제한하게 되는데, 그 이유는 edge가 담을 수 있는 정보는 Node간의 유사성보다 더 확장시킬 수 있기 때문입니다.

해당 논문에서는 Model의 Input으로 $X, A$ 를 직접적으로 활용하여 $f(X, A)$ 를 구성함으로써 $L_{reg}$ 부분을 제거할 수 있게 합니다. $f(\cdot)$을 adjacency matrix에 제한함으로써 supervised loss $L_0$ 에서 구할 수 있는 gradient를 분배할 수 있도록 하며 이는 label의 유무에 상관없이 node의 representation을 학습할 수 있게 합니다.

논문의 Contributions

Simple / Well-behaved layer wise propagation rule for neural network models
위의 이점은 Spectral graph convolutions의 1차 근사를 통해 달성할 수 있습니다.
Fast / Scalable Semi-Supervised Classification of nodes - 정확도와 효율성

Fast Approximate Convolutions on Graphs

GCN에서 Convolution에 해당하는 정의를 다음과 같이 표현하게 됩니다.

$H^{(l+1)} = \sigma (\tilde D^{-1/2} \tilde A \tilde D^{-1/2} H^{(l)}W^{(l)})$ ~(2)

로서 매 Hidden Layer와 layer-wise propagation rule을 정의합니다.

$\tilde A = A + I_N$: 자기 자신과의 관계까지 포함하는 Adjacency Matrix로서 기존의 Adjacency Matrix에서 Identity Matrix도 대각선 부분을 1로 채워 표현합니다.
$\tilde D_{ii} = \sum_j \tilde A_{ij}$: Degree Matrix를 Adjacency Matrix의 하나의 열을 통합하여 나타냅니다. 이 때 주의해야 할 점은 $A$ 에 대한 식이 아닌 $\tilde A$ 에 대한 식이기에 자기 자신과의 관계까지 포함하여 기존 Degree보다 +1이 더 추가됩니다.
$H^{(l)} \in R^{N \times D}: l^{th} \ Layer \ Activation \ Matrix$

하지만 (2)번 식의 꼴을 나타내기 위해선 본 챕터에서부터 설명하는 유도를 거치게 되는데, 간략하게 설명해보자면

“Eigendecomposition의 비용이 너무 커서 Chebyshev Polynomial로 근사해서 표현하겠다”입니다. 이는 매우 복잡한 내용이지만 최대한 Line-by-Line으로 공부해보고자 했습니다.

Spectral Graph Convolutions

Spectral Convolutions vs Spatial Convolutions

GCN은 두 가지 맛으로 나타납니다; Spectral GCN / Spatial GCN

이 둘의 차이점은 같은 GCN을 진행함에 있어 처리 방법에 차이가 있는 것인데, Spatial 먼저 살펴보겠습니다. Spatial GCN은 자신 주위의 local 이웃 노드의 Feature Value를 Aggregation 하는 방식으로 진행됩니다. 사실 어떻게 보면 Graph Neural Network 자체가 주위의 노드를 계산에 더 반영하기 위해서 사용하는거 아닌가 싶기도 하지만, Spectral GCN과 다르게 더 간단하고 Eigen 관련 개념을 사용하지 않는다고 합니다. 대표적으로는 GraphSAGE가 있지만 Spatial GCN은 본 논문에서 다루지 않으므로 넘어가겠습니다. (사실 Spatial GCN이 간단한 개념 상으로는 더 어울리긴 하지만…)

Spectral GCN에서는 각 노드의 Feature 값을 하나의 Signal로 간주합니다. Spectral이라는 말 자체가 ‘스펙트럼’에서 유래한 것으로 유추해볼때 결국 전기공학에서 많이 사용하는 신호처리와 관련되어 있으며, 이에 따라 Fourier Transform 개념이 자동으로 따라옵니다. 이에 대하여 이해하기 위한 개념들을 하나씩 정리해보겠습니다.

Laplacian

Laplacian의 의미는 위의 슬라이드로서 설명할 수 있습니다. 즉, 하나의 중심 노드와 해당하는 이웃 노드들 간의 차이를 한 번에 계산하기 위한 수단이며 관계의 압축체입니다. Laplacian Matrix의 주요 특징으로는 대칭행렬이기에,

$n$ 개의 eigenvalue들이 존재하며
Eigenvector가 real-value이고 직교한다.

의 속성을 갖고 있습니다. 그렇다면 Laplacian, $L$ 은 Eigen-decomposition이 가능하다는 뜻이므로, $L = f\Lambda f^T$ 로 분해할 수 있고 이를 반대로 적어보면, 아래와 같이 적을 수 있을 것입니다.

$f^TLf = \lambda_f = \sum\limits_{i,j}w_{ij}(f(i) - f(j))^2$

이 때, $L$ 에 양 옆에 $f$가 Eigenvector 인데, $f^TLf$ 의 의미가 결국 Laplacian에 대한 $f$ 의 Quadratic Form이므로 우측과 같이 Weighted Graph일 때, 각 노드 Feature Value의 차의 합이라고 할 수 있습니다. 결국 그래프에 대한 Laplacian을 구할 수 있다면 해당 행렬의 Eigenvector와 value를 구할 수 있고, Eigenvalue가 가장 작은 Eigenvector를 Feature의 값으로 지정한다면, Feature들간의 차이가 감소하게 될 것입니다. 이는 Node Similarity를 높이는 것이라 할 수 있습니다 (그렇다고 Eigenvalue가 0이 되는 것은 trivial solution이기 때문에 지양해야 합니다).

Signal, Graph Fourier Transform(GFT)

그럼 대체 위의 Laplacian이 Spectral, 또는 신호처리와 무슨 연관이 있을까요? 또한 음성 데이터에 많이 사용되어 음성 분해를 진행하는 Fourier가 왜 Graph에서 사용되는 지 모르겠습니다. 애초에 Graph내에 신호란 무엇일까요?

Graph내에 신호라는 것은 ‘차이’입니다. 마치 어둠 속에서의 빛이 더 의미가 있는 것처럼, 신호가 의미가 있으려면 어떤 차이의 값이 커야합니다. 그래프 내에서 노드 값의 차이를 지속적으로 관찰하기 때문에 Signal의 의미를 가지며, $x \in R^N$ 로서 Node Feature라고 할 수 있습니다.

Fourier Transform은 저 역시 자세한 정의를 모르지만 간단하게 원리를 나타내보자면, 하나의 신호를 주파수를 통해 분해를 진행하는 것이며, 이를 통해 저주파와 고주파를 나누는 것입니다. 주파수를 살펴보고자 하는 이유는 위에서 계속 언급하고 있는 값에 대한 차이를 살펴보고자 하는 의미가 있으며, 이를 Eigenvector로써 달성할 수 있습니다. 각 Eigenvector는 해당하는 Eigenvalue가 있고, Eigenvector를 곱했을 때 차이(주파수)가 크다면, Eigenvalue가 작습니다. 따라서 Signal을 Eigenvector에 곱하는 것 자체가 Signal에 Fourier Transform을 적용하는 것과 의미가 같으며, 이를 다음과 같이 표현할 수 있습니다.

$U^Tx$: Signal $x$ 에 Eigenvector를 곱해 Frequency로 변환하였다.

다음으로는 Filtering을 진행해야 합니다. $U^Tx$가 적용된 것을 보고 눈치채실 수도 있지만, 마치 Eigen decomposition을 통한 차원 축소를 진행하는 것 처럼, $\lambda$, 고유값을 선택하여 Filtering을 합니다. Graph를 통해 저희가 달성하고자 하는 것은 대부분 ‘차이가 적은 것’을 찾는 것이므로, 고유값이 작은 순서대로 선택해야하며 Laplacian은 decomposition을 진행했을 때, 고유값이 오름차순으로 정렬되기 때문에 위에서부터 선택하면 됩니다.

$g_\theta (U^Tx)$: Frequency에 Filter를 씌워 Eigenvalue 오름차순으로 선택

Filtered Frequency에 다시 Eigenvector U를 곱하게 되면 다시 Signal로서 되돌리는 꼴이 됩니다.

$U{g_\theta(U^Tx)} = Ug_\theta U^Tx \Rightarrow Lx$

결국 Graph의 Signal에 Graph Fourier Transform을 적용하여 Frequency로 변환한 뒤, Filtering을 씌워 다시 Signal로 변환하는 과정이 Laplacian 안에 포함되어 있는 것입니다. 하지만 이것을 곧이 곧대로 Laplacian으로 치환할 수 없는 이유는 Filtering 과정에서 발생한 Eigenvalue의 선택 때문입니다(Approximation).

Paper Notation

지금까지 설명한 개념들은 결국 논문의 Notation을 따라가기 위함이었습니다. 최종적으로

$g_\theta * x = Ug_\theta^* U^T x$ 이라는 식은 Graph Signal에 Spectral Convolution을 진행한 결과가 Laplacian을 활용한 결과값이라는 것을 알 수 있었습니다. Laplacian이 그래프의 본질을 밝히는 데에는 아주 좋은 행렬이지만, Laplacian의 Eigen Value / Vector를 계산하는 것의 계산 복잡도는 $O(N^2)$ 가 소요됩니다. 따라서 Eigen Decomposition에 소요되는 비용을 줄이기 위하여 Eigen value를 계산하는 함수인 $g_\theta(\Lambda)$ 를 Chebyshev 다항식 $T_k(x)$ 의 K차수까지로 근사하고자 합니다. ChebyShev에 대하여서는 저도 이해가 완전하지는 않지만 본 논문에서 해당 기법의 활용한 이유는 재귀를 통한 근사식이라는 것과, 초기값의 간단함인 것으로 사료됩니다.

$g_\theta’ \approx \sum\limits_{k=0}^K \theta_k’T_k(\tilde \Lambda)$ ~ Eigenvalue Function Approximation
$g_\theta’*x \approx \sum\limits_{k=0}^K \theta_k’T_k(\tilde L) x$

로 최종 결과가 나타나게 되며, $\tilde L = 2/ \lambda_{max}L - I_N$ 의 꼴로 Rescale 합니다. 해당 식에서 K라는 값이 중요한데, 그 이유는 Graph내의 K step 만큼 차이가 나는 노드들에 계산을 한정시킬 수 있다고 합니다.

Layer-Wise Linear Model

위에서 K가 중요한 파라미터라고 언급했는데, 결국 K = 1로 설정합니다. 이 뜻은 주위의 이웃의 거리를 1로 한정시키겠다는 뜻입니다. 그리고 이것을 Convolution의 개념으로 봤을때, Filter Size가 1인 Kernel을 사용하고 있다고 할 수 있습니다. 이 때, $\sum\limits_{k=0}^K$ 에 K = 1의 값이 삽입이 되므로, 0도 포함이 되는데 결국, 0 step이 포함된다는 뜻은, “자기 자신과 1 Step 차이의 이웃들”을 계산에 포함한다는 뜻이라고 할 수 있습니다.

따라서 K=1일 때 Approximation을 나열해보면,

$g_\theta’ * x \approx \theta_0’x + \theta_1’(L-I_N)x = \theta_0’x - \theta_1’D^{-{1\over2}}AD^{-{1\over2}}$

이 때, $\tilde L = 2/ \lambda_{max}L - I_N$ 에서 $\lambda_{max} \approx 2$ 로써 훈련 과정에서 변화할 것이라고 하며, Filter Parameter는 모든 그래프에서 공유가 되므로 $\theta = \theta_0’ = -\theta_1’$로서 나타낼 수 있습니다. 이에,

$g_\theta’ * x \approx \theta (I_N + D^{-{1\over2}}AD^{-{1\over2}})x$

로서 나타낼 수 있습니다. 하지만 해당 식을 지나치게 반복할 수록 Deep Neural Network Model에서는 가중치 폭발 / 소실의 문제를 겪을수가 있는데 이를 위하여 Renormalization Trick을 사용합니다.

$I_N + D^{-{1\over2}}AD^{-{1\over2}} \Rightarrow D^{-{1\over2}}\tilde AD^{-{1\over2}} with \ \tilde A = A + I_N \ and \ \tilde D_{ii} = \sum_j \tilde A_{ij}$

해당 식을 Generalize하고자 합니다. Signal $X \in R^{N \times C}$ 은 각 노드에 C 차원의 Feature Vector가 존재하며, Filter F가 다음과 같이 필터링을 진행합니다. 이 때 $\Theta \in R^{C \times F}$ 인 Filter Parameter 행렬이며, $Z \in R^{N \times F}$는 한 차례 Convolved 된 Signal Matrix입니다.

$Z = D^{-{1\over2}}AD^{-{1\over2}}X\Theta$

Semi-Supervised Node Classification

위의 증명을 통해 Adjacency Matrix를 포함한 Spectral Convolution이

$L = L_0 + \lambda L_{reg}, with \ L_{reg} = \sum_{i,j} A_{ij} |f(X_i ) - f(x_j)|^2 = f(X)^T \Delta f(X).$ ~(1)

의 $L_{reg}$ 항을 제거해주어 더 간단한 모델을 구축할 수 있게 해줍니다. 그리고 해당 방식은 Feature Vector $X$에서 담고 있지 못하는 정보인 ‘관계’를 더 많이 담고 있다면 큰 의미가 있을 것입니다.

Example

Symmetric Adjacency Matrix A를 전처리 단계에서 Self Loop / 정규화를 통해 $D^{-{1\over2}}\tilde AD^{-{1\over2}}$로 변환한 뒤 two-layer GCN을 구축하면 다음과 같습니다.

$Z = f(X, A) = softmax(\tilde A ReLU(\tilde AXW^{(0)}) W^{(1)})$
- $W^{(0)} \in R^{C \times H}$ : Input-to-Hidden Weight Matrix
- $W^{(1)} \in R^{H \times F}$: Hidden-to-Output Weight Matrix

이어서, Label된 데이터에 대한 Cross-entropy error는 다음과 같이 구성합니다.

$L = -\sum\limits_{l\in y_L}\sum\limits_{f=1}^F Y_{lf}lnZ_{lf}$

각 Weight인 $W^{(0)}, W^{(1)}$은 Gradient Descent를 통해 계산됩니다. 또한 논문에서는 mini-batch가 아닌 Full Batch를 통해 Gradient Descent를 사용했는데, 메모리가 허락해준다면 가능하다고 합니다. Adjacency Matrix A의 Memory 는 Edge의 수에 비례하여 $O(|\mathcal{E}|)$ 로서 나타낼 수 있습니다.

Implementation

GCN에 대한 구현은 Tensorflow로 진행되었으며 $Z = f(X, A) = softmax(\hat A ReLU(\hat A XW^{(0)}) W^{(1)})$ 식에 대한 구현을 Sparse-Dense Matrix 연산을 통해 이루어졌습니다. 따라서, 계산 복잡도가 $O(|\mathcal{E}|CHF)$ 가 되어, Graph Edge 개수와 비례하게 된다.

GCN은

Graph-Based Semi-supervised learning
Graph-Based Neural Networks

로부터 영감을 받아 탄생하였다고 합니다. 이에 따른 간략한 Overview를 진행하기에 옮겨보았습니다.

Graph-Based Semi-Supervised Learning

Graph Representation을 이용한 Semi-supervised learning은 많은 접근법이 존재했지만 대부분 다음의 두 카테고리에 해당하였습니다.

Graph Laplacian Regularization Approach
- Label Propagation (Zhu et al., 2003)
- Manifold Regularization (Belkin et al., 2006)
Graph Embedding-Based Approach
- Deep Semi-supervised embedding (Weston et al., 2012)

최근에는 Skip-gram model이나 DeepWalk와 같은 주위 노드들의 Embedding을 사용하는 기법들이 집중을 받았으며, LINE / node2vec은 DeepWalk를 더 정교하게 구축했습니다.

Neural Networks On Graphs

초기에 Graph Neural Network가 등장하기 이전에는 RNN이 그 역할을 했으며, 이는 Node의 Feature값이 수렴할 때까지 연속적인 Propagation function을 적용했습니다. 이후 GNN이 등장하고, 이에 Convolution을 얹는 노력들이 존재하였습니다.

Experiments

본 모델에 대한 실험은 다음과 같습니다.

Semi-supervised document classification in citation networks
Semi-supervised entity classification in bipartite graph extracted from a knowledge grapgh
an evalutation of
- various graph propagation models
- Run-time analysis on random graphs

Datasets

Revisiting semi-supervised learning with graph embeddings. In International Conference on Machine Learning (ICML), 2016.

실험 Set-up은 Yang et al.의 “Revisiting semi-supervised learning with graph embeddings”을 따랐다고 하며, 이에 대한 표는 Table 1에서 나타내고 있습니다.

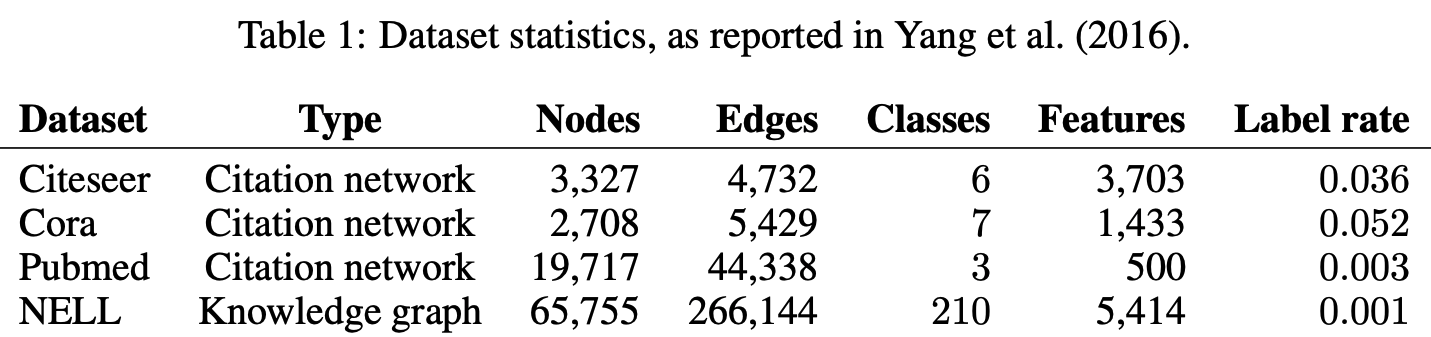
Citation Network Datasets

논문들의 인용 관계를 나타내는 데이터셋들은 Node가 Documents(논문)이며, Edge과 인용을 나타냅니다. Label rate은 각 데이터셋에서 훈련에 활용되는 training node를 전체 노드 개수로 나눈 것입니다.

데이터 셋들은 각 문서마다 Sparse한 Bag of words로 이루어진 feature vector로 이루어져 있으며, 문서들간의 Citation links를 담고 있습니다. Citation links가 (undirected)edge로 이루어져 있고, 이를 통해 Binary / Symmetric Adjacency Matrix A 를 구성할 수 있습니다. 각 문서들은 label을 갖고 있으며, 훈련을 위해 class마다 20개의 label을 사용하였지만 feature vector는 전체를 활용했습니다.

Citeseer
- 분류: 3312개 과학 논문, 6개의 Class로 분류
- 인용: Network가 4732개의 Link로 구성
- 단어: 3703 Unique한 단어가 0/1 vector로 표현
Cora:
- 분류: 2708개 과학 논문, 7개의 Class로 분류
- 인용: Network가 5429개의 Link로 구성
- 단어: 1433 Unique한 단어가 0/1 vector로 표현
Pubmed
- 분류: 19717개 과학 논문, 3개의 Class로 분류
- 인용: Network가 44338개의 Link로 구성
- 단어: 500 Unique한 단어가 TF/IDF Weighted Word Vector

Dataset	Classification	Citation Links	Uniqe Words
CiteSeer	3312 papers, 6 Class	4732 Links	3703 words-0/1 vector
Cora	2708 papers, 7 Class	5429 Links	1433 words-0/1 vector
Pubmed	19717 papers, 3 Class	44338 Links	500 words-TF/IDF Weighted Word Vector

Knowledge Graph Dataset

Knowledge Graph는 Directed / Labeled Edge들이 관계를 나타냅니다. Directed이기 때문에 relation node $r_1, r_2$ 에 대하여 $(e_1, r, e_2)$ 의 관계를 분리하여 $(e_1, r_1) / (e_2, r_2)$로 나타냅니다. Entity node들은 Sparse Feature Vector로 나타내며,
- NELL은 Knowledge Graph에서 추출된 Bipartite graph dataset으로서 55,864의 relation node들과 9,891 entity node로 이루어져있습니다.
Random Graphs

Epoch별 훈련 시간을 측정하기 위하여, Random Graph Dataset을 다양한 크기로 준비하여 실험해보았습니다. N개의 node를 가진 Dataset에 대하여 2N개의 edge를 random하게 할당하였으며, Identity Matrix $I_N$ 를 행렬 $X$ 의 Feature로 할당했습니다. 이를 통해 훈련에서 Feature에 대한 의존도를 제거하고 각 Node의 Label만 고려하는 훈련이 되는 것입니다.

Experiemental Set-Up

실험은 2-Layer의 GCN을 훈련시키고, 1000개의 Labeled 데이터에 대하여 prediction accuracty를 측정하였다. 10-Layer의 더 깊은 모델도 구축해보았으며, Yang et al.의 실험 세팅과 같이 500개의 Labeled 데이터에 대하여 Validation set으로 설정하여 Hyperparamter Optimization도 진행하였습니다.

Results

Semi-Supervised Node Classification

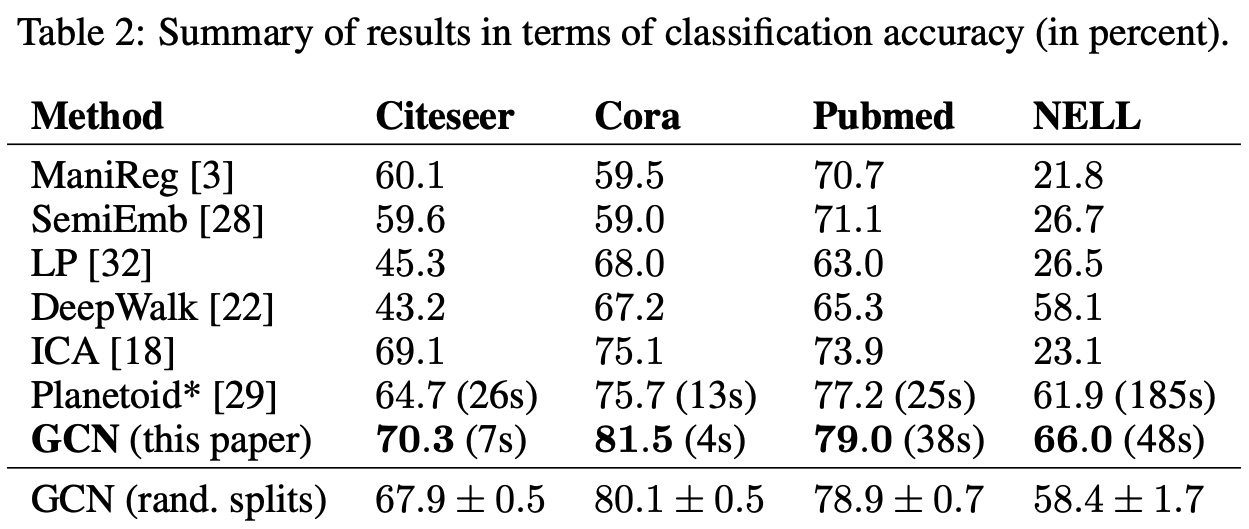
표에 나타난 숫자는 분류 정확도를 %로 나타내고 있습니다. 이전 모델들에 비하여, 모든 데이터셋에서 성능과 속도 면에서 GCN이 압도적으로 우수한 것을 살펴볼 수 있습니다.

Evaluation of Propagation Model (Ablation)

위에서 왜 그래프가 Signal 처리 기법인 Fourier Transform을 사용하는지, 그것을 왜 Chebyshev Filter를 거치고 1차 근사식, 파라미터 단일화, Renormalization Trick을 사용하는 것을 살펴봤습니다. 해당 방법들은 모두 Propagation Model이고, Multi-Layer Model에서 어떻게 다음 Layer로 정보를 전달할 지에 대한 방법입니다. 이에 대해서도 발전 순서별로 평균 분류 정확도를 나타내며, Weight Matrix Initializations를 거친 후에 100번의 trial을 거친 결과입니다.

Training Time Per Epoch

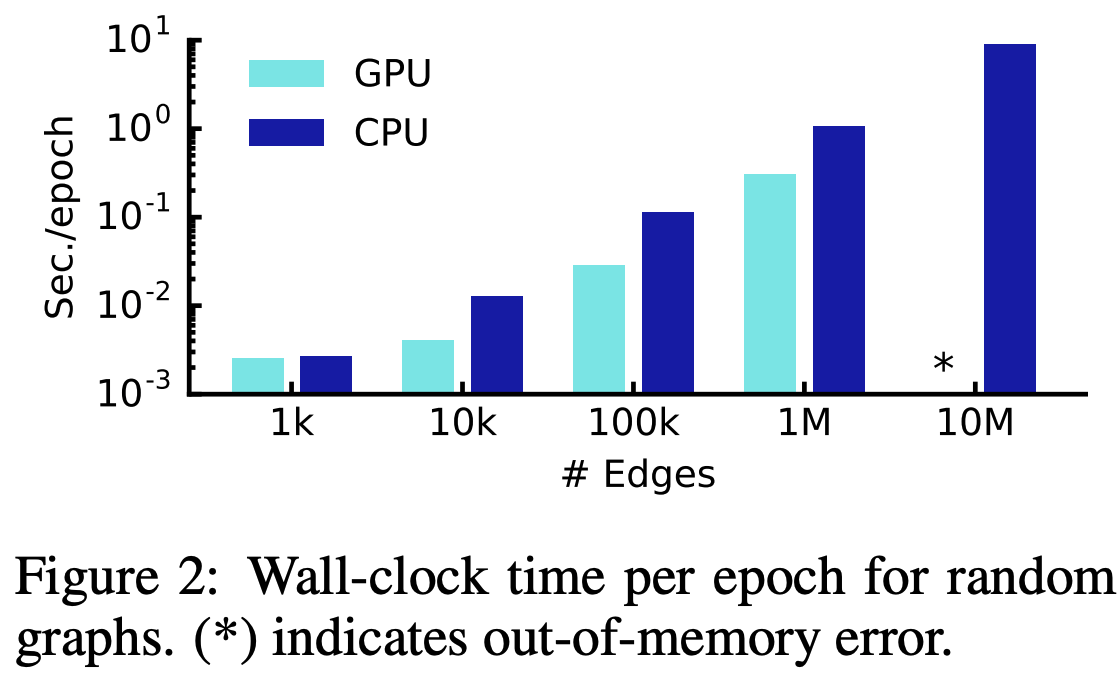
Figure 2에서는 Random Graph에 대한 Epoch당 평균적인 Training Time을 보여주고 있습니다. 이는 Forward Pass, Cross-Entropy 계산, Backward Pass에 대한 평균입니다.

Discussion

Semi-supervised Model

GCN 기법은 Semi-Supervised Node Classification 분야에서 다른 기법들보다 큰 Margin으로 성능이 좋았습니다. $L_{reg}$ 로 표현하였던 Graph-Laplacian 정규화에 기반한 모델들은 Edge들이 단순히 Node들의 유사성만을 담고 있다는 가정을 담고 있기에 Graph에 대한 이해를 완전히 할 수 없었다고 생각합니다. 또한 Skip-gram(hop)방식은 Multi-step pipeline을 따르고 있는데 이 역시 최적화가 어렵습니다. 하지만 GCN을 통하면 효율성 및 성능 모두 큰 개선을 이룰 수 있다고 합니다.

Pytorch Implementation

GCN을 위한 Pytorch 구현을 진행해보겠습니다. 본 구현은 저자가 직접 구현한 것을 기반으로 하고 있으나, 의아하게도 명백하게 잘못된 것이 있는데 수정이 안 된 것이 있었으며, 이는 본디 저자가 Tensorflow User이기 때문에 발생한 오류가 아닐까 싶습니다.

Dataset

먼저 Dataset은 Cora를 사용하였습니다. Cora Dataset 다운로드 링크 에서 cora.content와 cora.cites를 다운 받으며 각 데이터는 Node Feature, Class / Citation Link를 담고 있습니다. Cora 및 다른 데이터들도 content / cites의 구조로 이루어져 있기에, path와 dataset 이름을 파라미터로 받는 load_data 함수는 다음과 같은 절차를 따릅니다.

데이터 읽기
.content를 통해 Feature & Label / .cites를 통해 Link 추출하고 Graph를 구축
Edge로써 Adjacency Matrix 구축 후 Normalize($D^{-{1\over2}}AD^{-{1\over2}}$)
Train / Valid / Test Data의 Index를 설정하고 Return
Semi-supervised이기에 unlabaled data의 Feature 정보는 남겨야 합니다.

def load_data(path="../data/cora", dataset="cora"):
    print(f"Loading {dataset} dataset...")

    idx_features_labels = np.genfromtxt(
        f"{path}/{dataset}.content", dtype=np.dtype(str)
    )
    #     array([['31336', '0', '0', ..., '0', '0', 'Neural_Networks'],
    #        ['1061127', '0', '0', ..., '0', '0', 'Rule_Learning'],
    #        ['1106406', '0', '0', ..., '0', '0', 'Reinforcement_Learning'],
    #        ...,
    #        ['1128978', '0', '0', ..., '0', '0', 'Genetic_Algorithms'],
    #        ['117328', '0', '0', ..., '0', '0', 'Case_Based'],
    #        ['24043', '0', '0', ..., '0', '0', 'Neural_Networks']],dtype='<U22')
    # idx_features_labels는 1:-1이 Features / -1이 Labels로 나타난다.
    # Graph를 구축하기 위한 관계도는 .cites에 위치

    # 각 Features를 csr_matrix(compressed Sparse Row Matrix)로 변환
    # 각 Labels를 One Hot Encoding으로 변환
    features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
    labels = encode_onehot(idx_features_labels[:, -1])

    # csr_matrix: Compressed Sparse Row Matrix
    # coo_matrix: A sparse matrix in COOrdinate format

    # Build Graph
    idx = np.array(idx_features_labels[:, 0], dtype=np.int32)  # index for papers
    idx_map = {j: i for i, j in enumerate(idx)}                # index의 순차적 index

    edges_unordered = np.genfromtxt(
        f"{path}/{dataset}.cites", dtype=np.int32
    )                                                          # edges_unordered: 각 Paper가 가리키고 있는 Paper
    edges = np.array(
        list(map(idx_map.get, edges_unordered.flatten())), dtype=np.int32
    ).reshape(edges_unordered.shape)                           # edges들을 고유 index가 아닌 개수에 맞는 index 변환
    
    adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
                        shape=(labels.shape[0], labels.shape[0]),
                        dtype=np.float32)
    
    # Build Symmetric Adjacency Matrix
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

    features = normalize(features)
    adj = normalize(adj + sp.eye(adj.shape[0]))
    # Normalize의 과정 속에 Degree의 -1/2승을 곱해주는 것이 있는데, 이를 위해
    # 먼저 Adjacency Matrix A에 eye matrix를 더해주는 Renormalization Trick을 적용하는 것을 볼 수 있습니다.
    
    idx_train = range(140)            # Train은 0~140
    idx_val = range(200, 500)         # Validation은 200~500
    idx_test = range(500, 1500)       # Test 는 500~1500 Index를 가진 데이터

    features = torch.FloatTensor(np.array(features.todense()))
    labels = torch.LongTensor(np.where(labels)[1])
    adj = sparse_mx_to_torch_sparse_tensor(adj)

    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj, features, labels, idx_train, idx_val, idx_test

GCN 모델

GCN 모델에서는 $Z = D^{-{1\over2}}AD^{-{1\over2}}X\Theta$ , $Z = f(X, A) = softmax(\tilde A ReLU(\tilde AXW^{(0)}) W^{(1)})$ 를 구현함으로써 Renormalized Trick을 이용한 Laplacian Matrix로 인한 Convolution을 담고 있습니다. 따라서 해당 식의 절차를 그대로 따른다면 Graph Convolutional Network가 되는 것입니다. CNN처럼 Filter Size와 같은 것은 정하지 않아도 되며 심지어 계산 내에서 해당 사이즈가 1로 포함되어 있습니다.

GraphConvolution: Layer를 나타내고 있으며, $AXW$부분을 맡고 있습니다.
GCN: 해당 Layer들을 two-layer Model로 구성하고 Dropout, ReLU를 적용한 뒤, forward함수의 return 값으로 log_softmax를 나타내고 있습니다.

개념에 도달하는 과정 자체가 어려울 뿐, 구현하는 모델은 매우 쉽다고 느껴지는 모델이었습니다.

class GraphConvolution(Module):
    def __init__(self, in_features, out_features, bias=True):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = Parameter(torch.FloatTensor(in_features, out_features))
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)

    def forward(self, input, adj):
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support)
        if self.bias is not None:
            return output + self.bias
        else:
            return output

    def __repr__(self):
        return self.__class__.__name__ + ' (' \
               + str(self.in_features) + ' -> ' \
               + str(self.out_features) + ')'
               
class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout):
        super(GCN, self).__init__()

        self.gc1 = GraphConvolution(nfeat, nhid)
        self.gc2 = GraphConvolution(nhid, nclass)
        self.dropout = dropout

    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.gc2(x, adj)
        return F.log_softmax(x, dim=1)

Train & Validation

Train과 Validation을 진행할 때, 각기의 train / validation data에 대한 index를 설정합니다. 모델에서는 Features를 활용하는데 해당 부분은 indexing이 없으므로 전체 데이터들에 대한 feature를 사용하나, Loss와 Accuracy를 측정함에 있어서는 index를 통해 제어합니다. 따라서 Labeled / Unlabeled Data 모두 training에 참여하게 되는 Semi-supervised Learning이 가능하게 되는 것입니다.

hidden = 16
dropout = 0.5
lr = 0.01
weight_decay = 5e-4
cuda = True

if cuda:
    model.cuda()
    features = features.cuda()
    adj = adj.cuda()
    labels = labels.cuda()
    idx_train = idx_train.cuda()
    idx_val = idx_val.cuda()
    idx_test = idx_test.cuda()
    
model = GCN(nfeat=features.shape[1],
            nhid=hidden,
            nclass=labels.max().item() + 1,
            dropout=dropout)

optimizer = optim.Adam(model.parameters(),
                       lr=lr, weight_decay=weight_decay)

def train(epoch):
    t = time.time()
    for idx in tqdm(range(epoch)):
        model.train()
        optimizer.zero_grad()
        output = model(features, adj)
        loss_train = F.nll_loss(output[idx_train], labels[idx_train])
        acc_train = accuracy(output[idx_train], labels[idx_train])
        loss_train.backward()
        optimizer.step()
        
        if idx % 100 == 0:
            model.eval()
            output = model(features, adj)
            loss_val = F.nll_loss(output[idx_val], labels[idx_val])
            acc_val = accuracy(output[idx_val], labels[idx_val])
            print('Epoch: {:04d}'.format(epoch+1),
                  'loss_train: {:.4f}'.format(loss_train.item()),
                  'acc_train: {:.4f}'.format(acc_train.item()),
                  'loss_val: {:.4f}'.format(loss_val.item()),
                  'acc_val: {:.4f}'.format(acc_val.item()),
                  'time: {:.4f}s'.format(time.time() - t))
            
def test():
    model.eval()
    output = model(features, adj)
    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])
    print("Test set results:",
          "loss= {:.4f}".format(loss_test.item()),
          "accuracy= {:.4f}".format(acc_test.item()))

Training이 진행되면서, train loss와 validation loss가 감소하는 것을 살펴볼 수 있으며, Cora Dataset이 애초에 작은 데이터이기 때문에 실행시간도 빨라 mini-batch가 필요 없었습니다. Test Set에 대한 Loss / Accuracy는 다음과 같습니다.

Test set results: loss= 0.6021 accuracy= 0.8330

하지만 생각해보면, Mini Batch를 구성하기 위해선 매우 까다롭기도 합니다. 이것이 논문의 Limitation으로도 나타나있는데, Full Batch를 부분부분 쪼개기 시작하면 해당하는 노드들의 모든 관계를 가져와야하고 관계가 연결되어 있는 노드들도 배치에 포함시켜야 합니다. 따라서 해당하는 기법은 Future Work로 남겨두고 있습니다.

참고자료

GCN을 이해하기 위해서는 확실히 최종 식이 도출되기 위해 필요한 GFT, Chebyshev, Spectral Graph Theory 등 수많은 개념들이 필요했습니다. 이에 따라 하나의 개념을 이해하기 위해서 꼬리 물기 식으로 필요한 개념들이 많았는데 이에 참고자료의 양이 좀 많았습니다. 특히 Spectral Graph Theory의 1,2번째 포스트는 GCN을 공부할 때 읽으면 혜안을 주는 명 포스트라고 생각합니다.

Spectral Graph Theory

https://balcilar.medium.com/struggling-signals-from-graph-34674e699df8
https://web.media.mit.edu/~xdong/talk/BDI_GSP.pdf
https://people.orie.cornell.edu/dpw/orie6334/Fall2016/lecture7.pdf
https://towardsdatascience.com/tutorial-on-graph-neural-networks-for-computer-vision-and-beyond-part-2-be6d71d70f49
https://arxiv.org/pdf/1210.4752.pdf
https://openreview.net/pdf?id=CYO5T-YjWZV
https://balcilar.medium.com/spectral-feature-of-graph-signals-a54a244bab22

Spectral Graph Convolution

https://towardsdatascience.com/spectral-graph-convolution-explained-and-implemented-step-by-step-2e495b57f801
https://towardsdatascience.com/beyond-graph-convolution-networks-8f22c403955
https://ai.stackexchange.com/questions/14003/what-is-the-difference-between-graph-convolution-in-the-spatial-vs-spectral-doma
https://towardsdatascience.com/graph-convolutional-networks-for-geometric-deep-learning-1faf17dee008
https://towardsdatascience.com/tutorial-on-graph-neural-networks-for-computer-vision-and-beyond-part-2-be6d71d70f49

Overview

https://baekyeongmin.github.io/paper-review/gcn-review/
https://www.topbots.com/graph-convolutional-networks/?fbclid=IwAR2JLcWELhye46GEWvQu2i_RT2sLGxNpKZNeTXmeFfkLGQs51eE4crLVGRQ
http://tkipf.github.io/graph-convolutional-networks/
https://arxiv.org/pdf/1902.07153.pdf
https://cse291-i.github.io/Lectures/L13_Graph_CNN.pdf
http://web.cs.ucla.edu/~patricia.xiao/files/Reading_Group_20181204.pdf
http://dsba.korea.ac.kr/seminar/?mod=document&pageid=1&target=member_display&keyword=JonghyunChoi&uid=1329

Side Concepts

Adjacency: https://en.wikipedia.org/wiki/Adjacency_matrix#Matrix_powers
Convolution Theorem: https://en.wikipedia.org/wiki/Convolution_theorem